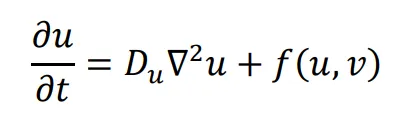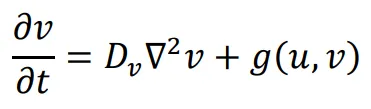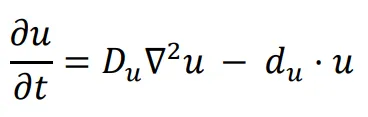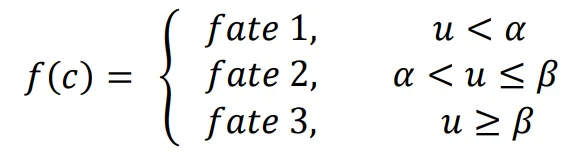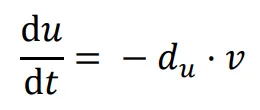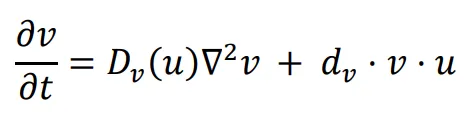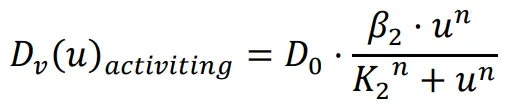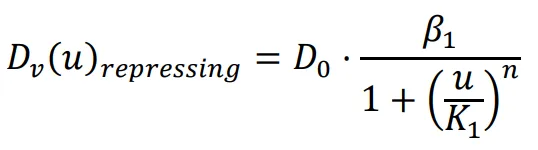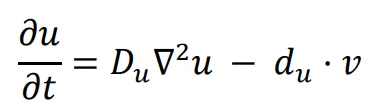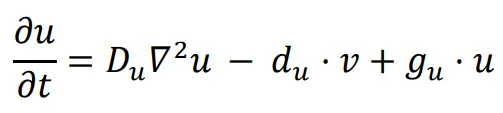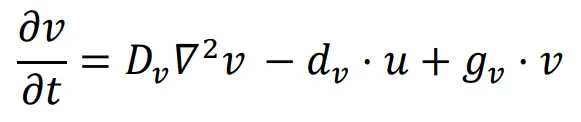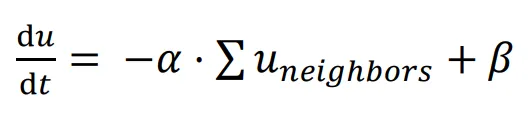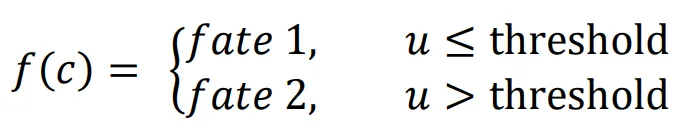1. Introduction
Pattern formation, the process of generating spatially ordered structures from an initially uniform or random state, is a vital aspect of biological development. This phenomenon is widespread across various tissue levels and organism types, and understanding the formation and function of these patterns is crucial for unraveling the principles of biological design and engineering. In 1952, Alan Turing proposed one of the most influential theories of pattern formation, which demonstrated that a system of two or more diffusible substances reacting with each other can produce stable spatial patterns under certain conditions [
1]. Other mechanisms, such as morphogen gradients, cell–cell contact signaling, and self-organization, can also generate complex and dynamic patterns that regulate the development, differentiation, and function of biological systems.
In recent years, synthetic biology has emerged as a powerful tool for studying and manipulating pattern formation in biological systems. Synthetic biology aims to design and build novel biological components, circuits, and networks that can perform specific functions or behaviors. By applying synthetic biology methods, researchers have managed to create artificial patterns in living systems by emulating natural mechanisms or inventing new ones [
2,
3,
4,
5,
6,
7,
8,
9]. Furthermore, synthetic biology can be employed to reverse-engineer natural patterns, facilitating an understanding of their underlying logic and function ().
. Overview of integrating in silico and wet lab approaches in pattern formation. The utilization of genetic circuits in bacteria or mammalian cells can yield patterns analogous to those obtained through computational simulations.
2. Turing Patterns and Self-organization
Over the years, various mathematical frameworks have been proposed to understand the phenomenon of pattern formation in nature. Among these frameworks, the Turing model, introduced by renowned British mathematician Alan Turing in the 1950s, has emerged as a fascinating paradigm that has been validated across multiple biological scales.
The concept of Turing patterns was first elucidated in Turing’s seminal paper, “The Chemical Basis of Morphogenesis” [
1], which offered insights into the mechanisms behind the emergence of intricate symmetrical and asymmetrical patterns in biological systems. Turing presented a theoretical model that relied on the interaction between two hypothetical chemical species—an activator and an inhibitor—within a reaction-diffusion system. He demonstrated that localized fluctuations in the concentrations of these chemicals, which he referred to as “morphogens”, can give rise to complex patterns.
The general form of Turing’s model can be described by two reaction-diffusion equations:
in the above equations,
u and
v represent the concentrations of activators and inhibitors, respectively.
Du and
Dv denote the diffusion coefficients, while ∇
2 signifies the second-order spatial diffusion, represented by the Laplace operator. The functions
f(
u,
v) and
g(
u,
v) describe the reaction, and their form and parameter values characterize the interaction between the activator and inhibitor.
Turing Patterns Exist Widely in Nature
Turing models have been found to effectively account for various natural phenomena involving pattern formation in the animal kingdom. For instance, one-dimensional patterning in cyanobacteria can be explained by a simple reaction-diffusion model composed of three components: HetL, HetR, and PatS [
10]. Additionally, the formation of human fingerprints has been attributed to the reaction-diffusion system of the WNT and BMP pathways, which govern cell migration and differentiation during early follicular development [
11]. Similarly, the striped patterns observed in the hair of cats and the distinctive spots of leopards have been linked to the Wnt–Dkk reaction-diffusion system [
12,
13]. Furthermore, the generation of regularly spaced transverse ridges in the palates of animals is believed to be controlled by a reaction-diffusion model involving fibroblast growth factor (FGF) as the activator and Sonic hedgehog (Shh) as the inhibitor [
14].
Beyond striped patterns, the Turing model has been implicated in various complex developmental processes. Notably, the spatial periodicity observed during
Drosophila development, described by the Turing-Child field, is a well-known example [
15] Similarly, the Turing-Child field has been employed to explain the symmetry and regularity in plant flower formation based on the ABC model of morphogenesis [
11]. The periodic expression of Sox9 during tracheal development is also thought to be associated with the Turing pattern [
12], and the Turing model has even been proposed as a theoretical framework for understanding the formation of the tarsal attachment microstructure in stick insects (Phasmatodea) [
13].
At a broader ecological level, ecologists have utilized the Turing model to elucidate patterns and dynamics in ecosystems. Early studies applied the Turing model to explain the patch distribution of plankton [
16]. Subsequently, mathematical models derived from the Turing model, considering the similarity between predator-prey interactions and activator-inhibitor dynamics, were employed to account for the temporal periodicity observed in predator and prey populations [
17].
The prevalence of Turing-like self-organization phenomena across different biological scales underscores the importance of studying the Turing model for comprehending the formation and evolution of life. Furthermore, insights gained from Turing pattern-like self-organization have the potential to inspire the design of biological materials and the creation of artificial living structures [
18,
19,
20]. By understanding the fundamental principles behind Turing patterns, researchers can apply these concepts to various fields, such as tissue engineering, biomaterials, and synthetic biology. This knowledge can lead to innovative solutions for medical treatments, environmental sustainability, and the development of novel materials with unique properties.
3. Pattern Is Determined by Morphogens
3.1. Gradient
3.1.1. Morphogen Gradient
The determination of cell differentiation in multicellular organisms is influenced by the presence and concentration of morphogens within their environment. Notably, in
Drosophila, the concentration of Decapentaplegic (Dpp) plays a pivotal role in the patterning of the anterior-posterior (AP) axis during the formation of wing imaginal discs [
21,
22]. Similarly, in Xenopus laevis, Bone Morphogenetic Protein 4 (BMP4) is responsible for the patterning of the dorsal-ventral (DV) axis in the mesoderm [
23]. Conceptually, this process can be abstracted into a physical model, where morphogens, which can be small molecules or peptides, diffuse through biological tissues, resulting in the establishment of concentration gradients. These gradients, in turn, determine the differentiation of cells into distinct types based on their location within the tissue.
Morphogen gradients are crucial for proper development, as they provide spatial information to cells and help establish the body plan and tissue organization. The gradients can be formed by various mechanisms, including passive diffusion, active transport, and localized production and degradation of morphogens. Once established, cells within the gradient can interpret the morphogen concentration through receptor-ligand interactions, which then trigger intracellular signaling cascades that ultimately lead to changes in gene expression and cell differentiation. By understanding the dynamics of morphogen gradients and their role in pattern formation, researchers can gain valuable insights into the fundamental processes of development, regeneration, and tissue repair.
A logic for cell fate determination by diffusible morphogens can be described below:
In the given equations:
- u represents the concentration of the morphogen
- Du is the diffusion coefficient
- ∇2 is the second-order spatial diffusion represented by the Laplace operator.
- du·u implies that morphogen u will spontaneously degrade over time
The equation
f(
c) describes how cell fate is determined by the morphogen concentration u. In this scenario, it is assumed that cells can decide between three fates based on the concentration of u at their location.
1. If the concentration of
u does not reach the threshold
α, cells do not differentiate (fate 1).
2. If the concentration of
u is higher than the threshold
α and lower than
β, cells differentiate into fate 2.
3. If the concentration of
u reaches the threshold
β, cells differentiate into fate 3.
By using these equations, researchers can model how morphogen gradients determine cell fate during development. The equations capture the essential elements of morphogen-guided cell differentiation: diffusion, degradation, and threshold-dependent responses. This mathematical representation can be useful for understanding and predicting the formation of tissue patterns and the organization of multicellular organisms.
Indeed, the simulation results offer valuable insights into the role of morphogen gradients in controlling cell differentiation and pattern formation. The distinct differentiation states observed in the model—fully differentiated, semi-differentiated, and undifferentiated—correspond to the concentration levels of the morphogen in different regions (depicted in ). This spatial dependence of cell fate determination is a crucial aspect of tissue development and organization in multicellular organisms.
The simulation demonstrates the power of morphogen gradients in orchestrating cell differentiation and tissue patterning. By establishing concentration gradients, morphogens create a positional information system that guides cells to adopt specific fates based on their location within the developing tissue. This process is essential for the formation of complex structures and the proper functioning of biological systems.
These findings not only reinforce the importance of understanding morphogen gradients in developmental biology but also have broader implications for tissue engineering, regenerative medicine, and the study of diseases related to abnormal cell differentiation. By gaining a deeper understanding of the mechanisms underlying morphogen-guided cell fate determination, researchers can develop new strategies to manipulate cellular behavior for therapeutic purposes and advance our knowledge of tissue development and repair.
. Illustrates the simulation of cell growth and differentiation in a 10 × 100 area over 500 unit times. In this example, the concentration of morphogen u spreads from left to right along the x-axis with the initial concentration of 1, the diffusion coefficient Du is 0.1; the threshold β is 10 times that of α (α = 0.0001). Periodic boundary condition is used. Top panel: The simulation result of morphogen concentration distribution. - White represents the maximum concentration. - Black represents a concentration of 0. This panel shows how the morphogen concentration forms a gradient, with the highest concentration on the left side (white) and decreasing concentration towards the right side (black). Bottom panel: The simulation result of cell differentiation based on morphogen concentration. - Yellow represents fully differentiated cells (fate 3). - Dark green represents undifferentiated cells (fate 1). - Light green represents semi-differentiated cells (fate 2). This panel demonstrates how cells differentiate according to the morphogen concentration. Cells near the high-concentration region (left side) differentiate into fate 3 (yellow), while cells in the middle region with intermediate concentration differentiate into fate 2 (light green). Cells in the low-concentration region (right side) remain undifferentiated (dark green). This simulation provides a visual representation of how morphogen gradients direct cell differentiation and pattern formation in a developing tissue. It highlights the importance of understanding the role of morphogens in the organization and development of multicellular organisms.
. The impact of varying morphogen diffusion coefficients and cell differentiation thresholds on the resulting pattern of cell differentiation. In all the simulations, threshold β is assumed to be 10α. The initial and boundary condition is the same as the simulation shown in .
showcases the significant influence of altering the morphogen diffusion coefficient
Du and cell differentiation threshold (
α) on the resulting patterning outcomes. By modifying these parameters, the model demonstrates the sensitivity of the patterning process to both the diffusion properties of the morphogen molecule and the cellular response threshold.
There are several experimental approaches to manipulate these parameters:
1. Increasing the diffusion coefficient
Du by attaching a tag peptide to the morphogen to modify its diameter, which could affect the distribution and spread of the morphogen concentration gradient.
2. Adjusting the strength of the transcription promoter to regulate the cell differentiation threshold (
α). This can influence the morphogen concentration required for cells to differentiate, altering the final pattern of cell differentiation states.
3. Manipulating the binding affinity between the morphogen and its receptors can also impact the cell differentiation threshold (
α). By modifying the sensitivity of the receptors, it is possible to control the cellular response to varying morphogen concentrations.
These experimental techniques emphasize the tunable nature of the patterning process. By understanding and controlling these parameters, researchers can manipulate cell fate determination and tissue organization, with potential applications in fields such as developmental biology, tissue engineering, and regenerative medicine.
3.1.2. Chemical Gradient and Cell Movement
Chemotaxis indeed plays a significant role in the movement of single cells, such as bacteria, in response to chemical gradients present in their environment [
24]. This phenomenon has the potential to be harnessed for artificial pattern formation and has been observed in various organisms, including
E. coli. The formation of a chemotaxis ring on an agar plate is a prime example of how
E. coli responds to chemical gradients in its environment [
25]. This pattern formation results from the specific movements of individual bacteria through the run-and-tumble model. The run-and-tumble model consists of two primary movement states:
1. “Run”: This state is characterized by persistent, long-distance motion, where the bacteria move in a relatively straight line.
2. “Tumble”: This state involves random steering movements, causing the bacteria to change direction.
As bacteria navigate through their environment, they continuously switch between these two states based on the perceived changes in chemical concentration. This decision-making process is mediated by an intricate signaling pathway, which allows bacteria to sense the changes in chemical gradients and adjust their movement accordingly.
When a bacterium senses an increase in the concentration of an attractant chemical, it tends to prolong its “run” state and move toward the higher concentration. Conversely, if the bacterium senses a decrease in the attractant concentration, it is more likely to enter the “tumble” state and change direction.
By understanding the mechanisms underlying bacterial chemotaxis, researchers can explore the potential applications of this phenomenon in various fields, such as microbiology, environmental bioremediation, and even in the development of synthetic biology-based systems for specific tasks, such as targeted drug delivery or biofilm disruption.
Accurately simulating the run-and-tumble motion of bacteria can be computationally intensive due to the large number of individual particles involved. Simplifying the modeling process is often necessary to make the simulations more tractable and efficient. Using the diffusion equation to simulate bacterial movement is a common approach that simplifies the representation of bacterial chemotaxis while maintaining the essential dynamics influenced by chemical gradients. In this method, the presence of chemicals in the environment affects the speed of bacterial motion, which corresponds to adjustments in the diffusion coefficient (
D).
By utilizing the diffusion equation, the simulation can capture the overall behavior of bacterial chemotaxis without the need to model the intricate details of individual run-and-tumble events. This simplification allows researchers to analyze the impact of chemical gradients on bacterial movement, explore various scenarios, and make predictions about the behavior of bacterial populations in different environments.
However, it is important to note that the diffusion-based approach is an approximation and may not capture all the nuances of bacterial chemotaxis, particularly in cases where individual cell behavior or specific interactions between cells and their environment are crucial for understanding the system. In such cases, more detailed individual-based models or hybrid modeling approaches may be required to obtain a comprehensive understanding of the system’s behavior. Nevertheless, the diffusion-based approach provides a valuable tool for studying bacterial chemotaxis in a more computationally efficient manner, enabling researchers to gain insights into the role of chemical gradients in bacterial movement and pattern formation.
We assume that in the initial state, chemical
u is uniformly distributed on the x-axis. To model a network where bacteria sense the environmental chemical
u gradient and change their movement speed accordingly, you can incorporate the chemotaxis response into the bacterial behavior.
That is, chemical
u is degraded by bacteria
v at rate
du. The bacteria
v spread on the plane, the diffusion coefficient is
Dv, and the bacteria grow (
dv > 0) or die (
dv < 0) under the influence of the chemical substance u according to the parameter
dv.
The diffusion coefficient, which influences the movement speed of bacteria, is determined by the previously mentioned functions. The repressing Hill equation is used to model the diffusion coefficient of the chemical that inhibits bacterial movement, while the activating Hill equation is used for the chemical that promotes bacterial movement. In this particular case, the Hill coefficient is chosen as an illustrative example of positively cooperative binding (
n > 1) that reflects a common occurrence in nature, where the value of
n is set to 2.
K1 and
K2 represent the repression and activation coefficients, respectively, which correspond to the concentration of the chemical
u when half-maximal repression or activation is achieved.
β1 and
β2 denote the maximal expression levels of the activator and repressor, respectively.
D0 refers to the original diffusion coefficient of bacteria that are unaffected by the chemical
u.
Based on the simulation results shown in , it is evident that when the chemical
u promotes bacterial movement and growth, the distribution of the bacterial population aligns with the chemical gradient. Conversely, when the chemical
u inhibits bacterial movement and growth, the bacteria form a low-concentration band in the region with intermediate concentrations of chemical
u.
Similarly, the chemical gradient can be generated through diffusion. Assuming that
Du represents the diffusion coefficient of the chemical substance
u, the diffusion of this substance within the region can be characterized by the following equation.
The result of spontaneous diffusion of chemical species to form a gradient (see ) is similar to that of an initial given gradient.
. Simulation results of bacterial movement represented by diffusion equation. The initial state assumes that cells grow uniformly in a 10 × 100 area and run for 300 time units; D0 = 0.001, β1 = 0.1, β2 = 1, K1 = K2 = 0.01. Periodic boundary condition is used. For activating effect simulation (Positive effect), select dv > 0 and use Dv (u)activating to calculate the diffusion coefficient of each grid; for repressing effect simulation (Negative effect), select dv < 0 and use Dv (u)repressing to calculate the diffusion coefficient of each grid. For chemical gradients, white indicates high concentration and black for low concentration; for cell concentrations, yellow indicates relatively high concentration and green indicates relatively low concentration.
. Simulation results of the concentration gradient formed by the spontaneous diffusion of chemical u with Du = 0.1. The initial state involves adding chemical u to a 1-unit-width strip in the center and running the simulation for 70 time units. Other conditions are same as the simulation in .
The reaction-diffusion model is well-known for its ability to generate the classic Turing pattern. A basic reaction-diffusion model requires at least two interacting morphogens [
1]. The FitzHugh-Nagumo (FHN) model, commonly found in academic textbooks, serves as a prominent example of the reaction-diffusion framework, particularly in characterizing neuronal spiking dynamics on a two-dimensional (2D) substrate [
26,
27]. Furthermore, Meinhardt and Gierer theoretically showed that a stable pattern can emerge from a system composed of two morphogens with localized self-activation and lateral inhibition in 2000 [
28]. Hence, to design a simple reaction-diffusion system for patterning, only two linear interactions need to be added to the diffusion equation of the two morphogens. For instance, the following equation describes a self-activating and mutually inhibiting network.
In this network, the diffusion coefficient of
u,
Du, is four times larger than the diffusion coefficient of
v,
Dv. Both the signal,
u, and the reporter,
v, have the same inhibition rate (
du =
dv) and the same self-activation rate (
gu =
gv). This represents the simplest form of the Gierer-Meinhardt model, while the simulation of patterning is presented in .
. Simulation results of the reaction-diffusion model. Two 100 × 100 random matrices were generated as the initial states of u (left panel) and v (right panel), and the simulation was run for 500 time units. Du = 0.001, Dv = 0.005, du = dv = 0.01, gu = gv = 0.02. Periodic boundary condition is used. White and yellow indicate high levels, while black and green represent low levels.
The complexity of patterns attainable in a reaction-diffusion system increases with the addition of more morphogens, variations in diffusion coefficients, and the introduction of derived interaction functions. Notably, incorporating an extra morphogen into a system with two morphogens has been shown to yield an extensive array of 475 distinct node networks capable of pattern formation, as demonstrated by Zheng et al. in 2016 [
29]. This finding highlights the rich potential for pattern generation and the vast design space available within multi-morphogen reaction-diffusion systems.
3.1.3. Cell–cell Contact Signaling
Apart from pattern formation observed in Turing-like systems, cellular patterning can also emerge through the transmission of information via direct cell–cell contact. These contact-dependent patterns might not rely on the diffusion of free morphogens, leading to unique mathematical characteristics that differ from traditional reaction-diffusion systems.
Delta-Notch Signaling
The Notch signaling pathway, considered a crucial lateral signaling circuit, serves as a highly conserved mechanism for intercellular communication. Its functionality depends on the interaction between DSL (Delta/Serrate/lag-2) family ligands on the surface of neighboring cells and the Notch receptor. When the ligand binds, the Notch receptor undergoes proteolytic cleavage, which activates or inhibits downstream gene expression, thus influencing cellular differentiation processes [
30,
31,
32]. Importantly, since the delta ligand remains confined to the cell membrane, the signaling event is localized and does not exhibit diffusion, affecting only neighboring cells. As a result, the mathematical model used to describe delta-notch signaling fundamentally differs from the reaction-diffusion model.
Similar to the Gierer-Meinhardt model, a basic Delta-Notch patterning model can be constructed with one type of cell inhibiting its neighbors.
In this network, the signal
u represents the expression of the Delta ligand, which is inhibited by the signal
u expression of neighboring cells, with
α representing the inhibitory rate and
β representing the constitutive expression rate. Cells are assumed to be hexagonal, and only ligands from cells in direct contact can bind to the receptor; hence, only signal
u from the six neighbors surrounding the cell are considered. The function
f(
c) describes the cell fate decision affected by signal
u: cells with an expression level of
u greater than a threshold enter the differentiated state, while cells with a lower expression level maintain their undifferentiated state.
The simulation results presented in showcase the impact of varying inhibitory rates on pattern formation. When the lateral inhibition effect is minimal (inhibitory rate,
α = 0.001), the 2D cell plane exhibits a stripe pattern with a width of approximately 2 cells. Within a broader range of inhibitory rates (
α = 0.01, 0.1), the 2D cell plane forms a stripe pattern with a width of 1 cell. However, if the inhibitory rate is either excessively low (
α = 0.0001) or excessively high (
α = 0.5), the network fails to establish a stable pattern. This example clearly illustrates the dependence of pattern formation on parameter values and emphasizes the significance of parameter adjustment in determining the formation or absence of patterns. The simulation results highlight the importance of fine-tuning the inhibitory rate to achieve desired cell patterning in the context of the Delta-Notch signaling pathway. The findings also underscore the critical role of lateral inhibition in regulating cellular differentiation and spatial organization.
. Simulation results of lateral inhibition, run for 200 time units; β = 0.1, threshold = 4. One cell was seeded at the center of the area in the initial state. In each running step of the time unit, every cell with fewer than 6 neighbors have the potential to grow a new cell in the empty neighboring space. The new cell will inherit the expression level of signal u from its parent. Different inhibitory rates (α = 0.0001, 0.001, 0.01, 0.1, 0.5) were simulated respectively, and the threshold is set at 1.0.
4. Pattern Formation in Synthetic Biology Systems
Pattern formation within synthetic biology systems stands as a central focus for synthetic biologists. Researchers have made significant progress by constructing biological circuits and networks using natural or modified morphogens, leading to the realization of artificial pattern formation in both prokaryotes and eukaryotes.
Through the manipulation of genetic circuits and/or regulatory elements, researchers can exert control over the expression of morphogens, thereby achieving desired spatial arrangements and morphological outcomes. This forward engineering approach enables the design and construction of synthetic biological systems with specific patterns and behaviors.
At the same time, researchers investigate the characteristics of natural systems, such as morphogen gradients, quorum sensing circuits, or cell–cell contact signaling, to uncover the fundamental principles underlying pattern formation. By applying these principles, they construct synthetic systems that mimic or reproduce natural pattern phenomena. This reverse engineering approach enhances our understanding of the mechanisms driving natural pattern formation and provides insights for constructing artificial biological systems with desired pattern formation capabilities.
Potential applications of synthetic biology in pattern formation extend to diverse fields, including tissue engineering, regenerative medicine, drug delivery, and biofabrication. By integrating the knowledge gleaned from both forward and reverse engineering approaches, synthetic biologists can develop novel solutions and tools for addressing complex biological challenges and advancing the field of synthetic biology.
4.1. Pattern Formation by Forward Engineering
Self-organization and Natural Morphogen Gradient: Stem-cell-based Embryo Models
Stem-cell-based embryo models (SCBEMs), occasionally termed ‘stem cell-based embryo model’ despite not involving synthetic gene circuits, have emerged as a highly promising technology for studying the developmental processes of organisms. The underlying concept of these models revolves around the ability of various types of stem cells to undergo self-organization and differentiate into distinct cell types under the influence of natural morphogen pathways, thereby mimicking the structural formation observed in natural embryos [
2,
3,
33,
34].
In these models, researchers use pluripotent stem cells (PSCs), such as naïve, extended or primed PSCs as well as extra-embryonic stem cells, as the starting point for generating embryos-like structures [
35,
36]. These cells possess the ability to differentiate into various cell types and self-organize into complex structures, which can resemble early stages of embryonic development.
The SCBEMs are achieved by providing an appropriate microenvironment, such as a 3D culture system, and introducing specific morphogens, growth factors, or small chemicals to guide cellular differentiation and organization. By carefully controlling the spatial and temporal distribution of these morphogens, researchers can recapitulate the natural morphogen gradients observed in real embryos, allowing the pluripotent stem cells to form embryo-like structures with correct spatial organization and cell type specification.
This forward engineering approach has several advantages, including the ability to manipulate and study the effects of specific morphogens on the developmental process, creating complex tissue constructs for regenerative medicine, and reducing the ethical concerns associated with using real embryos for research purposes.
However, there are also challenges in stem-cell-based embryo models, such as achieving a high degree of control over the morphogen gradients and fully understanding the complex interactions between various signaling pathways during embryonic development. Despite these challenges, stem-cell-based embryo models represent a powerful tool for investigating the fundamental principles of pattern formation and advancing the field of synthetic biology.
The successful conversion of spatial information into gene expression information through morphogen gradients was first achieved in 2014 using human embryonic stem cells (hESCs) [
2]. In this ground-breaking study, observable morphological changes were induced in hESCs cultured in a two-dimensional environment after treatment with 50 ng/mL BMP4 for 24~48 h (see ). Immunofluorescence imaging of CDX2, BRA, and SOX2 revealed a characteristic spatial pattern reminiscent of human germ layers during gastrulation [
37].
. A diagram of CDX2, BRA, SOX17, and SOX2 gradients and germ layer differentiation in 2D cultured hESCs [
2]. In this experiment, 2D cultured hESC on micropatterned coverslip was treated with BMP4 for 24 h. The fluorescence intensity of CDX2, BRA, and SOC2 showed germ layers differentiation (adapted from Warmflash et al. [
2,
38]).
In the context of the hESC study, the morphogen gradients induced by BMP4 treatment generated a spatial distribution of gene expression that resembles the “French flag” pattern, which was proposed by Lewis Wolpert in 1969 and represents a simple way to describe how cells in an embryo can interpret positional information and differentiate into distinct cell types [
38]. However, the complete understanding of how hESCs interpret the BMP4 morphogen gradient and differentiate into distinct cell types based on their position within the gradient is yet to be fully determined [
39].
This ground-breaking study demonstrated the potential of manipulating morphogen gradients to control the spatial patterning of gene expression in hESCs, which could have significant implications for understanding embryonic development and advancing the field of synthetic biology. By elucidating the mechanisms underlying morphogen gradient formation and cellular interpretation, researchers can gain valuable insights into the processes governing cell fate determination and pattern formation in developing organisms.
Following the seminal study on two-dimensional (2D) germ layer differentiation, further advancements in the field have led to the emergence of more complex embryonic-like structures through stem cell self-organization and the establishment of morphogen gradients in 3D structures. The pioneering work in creating a stem-cell-based embryo model was published by Harrison et al. in 2017, where a mixture of embryonic stem cells (ESCs) and trophoblast stem cells (TSCs) was cultured in Matrigel, resulting in their self-organization into three-dimensional (3D) structures that progressed to the E5.5 developmental stage [
3].
Since the initial breakthroughs in stem-cell-based embryo models, the methodology for constructing these models has undergone significant improvements. Recently, significant progress has been achieved in the establishment of standardized methodologies for cultivating stem-cell-based embryo models that faithfully replicate essential stages of post-implantation human embryonic development. These intricate models traverse key phases, starting with pre-gastrulation events where extra-embryonic compartments play a pivotal role as signaling hubs, guiding the precise specification of cell fate. They seamlessly progress through the establishment of polarity, the initiation of gastrulation, and ultimately reach stages reminiscent of the early phases of organogenesis [
40,
41,
42,
43,
44,
45,
46] (depicted in ).
Moreover, Naive human pluripotent stem cells (PSCs) have demonstrated a fascinating capacity for self-organization, giving rise to structures resembling blastocysts, referred to as blastoids [
47,
48,
49]. These advancements demonstrate the versatility of stem cell types that can be used to generate ‘stem cell-based embryo model’ [
50] and further expand the potential applications of these models. Meanwhile, other species, such as bovine [
51] and cynomolgus monkey [
52], are becoming involved in the field of stem-cell-based embryo models. This diversification of species in ‘stem cell-based embryo model’ research allows for a broader understanding of embryonic development across different organisms and the conservation or divergence of developmental mechanisms among them.
Overall, the significant improvements in stem-cell-based embryo models have expanded the potential applications of these models for studying developmental processes, tissue engineering, and regenerative medicine. As the field continues to advance, researchers will be able to gain a deeper understanding of the complex interactions between signaling pathways and cellular behaviors during embryonic development, potentially leading to new therapeutic approaches and insights into the fundamental principles of biology.
. Representative stem-cell-based embryo models (adapted from Oh et al. [
53]).
Artificial morphogen replacement, such as the use of GFP morphogen gradients, is another approach in forward engineering patterning that replaces natural morphogens with artificial ones. This method has been demonstrated in studies by Stapornwongkul et al. and Toda et al. [
61,
62], which successfully established artificial GFP gradients to substitute natural morphogen gradients in
Drosophila melanogaster wing imaginal discs and in vivo pattern formation.
In the study by Stapornwongkul et al., the researchers engineered Tkv and Put receptors to bind GFP dimers by fusing them with anti-GFP nanobodies [
61]. This allowed GFP to act as a morphogen instead of Dpp, rescuing wing development in Dpp-inactivated
Drosophila larvae. The GFP signaling gradient was further expanded through the incorporation of non-signaling receptors, resulting in improved wing morphology in adult flies.
Toda et al. introduced a novel system for pattern formation utilizing artificial GFP gradients [
62]. They employed two non-competitive anti-GFP Nanobodies, with one acting as the anchor-binding domain and the other as the receptor-binding domain. The receptor-binding domain was linked to a modified Notch receptor termed synNotch, which will be explained in detail later in Section 4.2.2. Upon simultaneous binding of GFP to both the anchor and receptor-binding domain, the synNotch receptor was activated, influencing downstream gene expression and enabling in vivo pattern formation through the establishment of predetermined GFP gradients.
These studies demonstrate the potential of artificial morphogen replacement as a powerful tool for studying developmental processes and tissue engineering. By utilizing artificial morphogen gradients, researchers can gain valuable insights into morphogen signaling, gradient formation, and cellular responses. This approach could also help to advance synthetic biology, regenerative medicine, and the development of novel therapeutic strategies.
4.2. Pattern Formation by Reverse Engineering
4.2.1. Reaction-diffusion Patterning: AHL Quorum Sensing Circuit
Using the principles of reverse engineering, Turing-like patterns can also be achieved through completely artificial circuits created from scratch. In a
Science article by Liu et al. in 2011, a quorum-sensing circuit based on a small-molecule AHL (acyl-homoserine lactone) was established, allowing for bacterial patterning by controlling the motility of
E. coli cells [
4].
The quorum-sensing system utilized in this study was initially discovered in
Vibrio fischeri, where the gene luxI expresses the small molecule AHL, which is then secreted. When the extracellular concentration of AHL reaches a high level, AHL binds to the LuxR protein, forming an AHL-LuxR dimer that activates the expression of target genes [
63]. Liu et al. employed AHL-LuxR to activate the expression of the repressor cI, which, in turn, repressed the expression of the bacterial motility-controlling gene cheZ. The low expression level of cheZ resulted in the bacteria remaining in a tumble state, thereby suppressing cell movement [
64]. By manipulating this AHL-based quorum-sensing circuit, the researchers were able to engineer bacterial patterns reminiscent of Turing patterns. This work demonstrates the potential of synthetic biology to create artificial circuits that mimic natural pattern-forming processes. This approach not only expands our understanding of the fundamental principles governing pattern formation in biological systems but also opens up new possibilities for the development of novel strategies in the fields of synthetic biology, tissue engineering, and regenerative medicine.
It is indeed important to highlight that the model in question, as presented by Liu et al., incorporates the consideration of nutrient concentration, as indicated in A. However, it should be noted that the equation does not account for the chemotaxis of the nutrient gradient. This omission is a consequence of the engineered strain used in the study, wherein the original cheZ gene, responsible for chemotaxis, was intentionally deleted. As a result, the engineered strain lacks the capacity for chemotaxis.
Notably, C of the study depicts the control strain, which is expected to possess an intact cheZ gene. The presence of a condensed ring observed in the control strain aligns with the characteristic phenomenon of a chemotaxis ring [
65]. The chemotaxis ring is a result of the bacteria’s response to the nutrient gradient, which causes the bacteria to move toward regions with higher nutrient concentrations. By deleting the cheZ gene in the engineered strain, the researchers effectively removed the chemotaxis behavior, allowing them to focus on the effects of the AHL-based quorum-sensing circuit on the bacterial patterning. This approach facilitated the study of the engineered circuit’s role in creating Turing-like patterns without the confounding effects of chemotaxis.
. Sequential patterning of
E. coli with a quorum-sensing circuit of AHL sensing and motility control [
4]. (
A) The motility control circuit based on AHL quorum-sensing. (
B) The establishment of a stripe pattern while the cell population expands. (
C) The control strain without the quorum-sensing circuit cannot form a pattern (adapted from Liu et al. [
4]).
4.2.2. Cell–cell Contact Patterning: synNotch Signaling
In a notable study published in 2016 by Morsut et al. in Cell, an artificial Notch signaling pathway known as “synNotch” was introduced [
5]. The researchers established a modular synthetic Notch platform that enables customization of both the input and output by swapping the recognition domain and effector components (depicted in A). Different from the morphogen gradient formed by diffusible GFP, the synNotch system relies on direct cell–cell contact signaling, meaning that free ligands cannot activate the receptor. This characteristic makes the synNotch system suitable for investigating signaling processes that specifically require cell–cell contact.
Additionally, the synNotch system incorporates a cis-inhibition mechanism, similar to that observed in natural Notch signaling [
66]. This cis-inhibition feature allows the system to achieve both lateral activation and self-inhibition within a single genetic circuit. This capacity makes the synNotch system a powerful tool for studying the dynamics of cell–cell contact signaling and its role in tissue patterning, development, and homeostasis.
As a versatile and customizable platform, the synNotch system has the potential to advance synthetic biology and tissue engineering by providing a framework for designing and implementing novel signaling pathways that can be tailored to specific applications. By combining the synNotch system with other synthetic biology tools and approaches, researchers can gain a deeper understanding of cell–cell contact signaling and its role in complex biological processes, ultimately leading to new therapeutic strategies and insights into fundamental principles of biology.
. The lateral activation circuit with synNotch bioparts [
5,
62]. (
A) Direct cell–cell contact. The notch core will release the effector (shown as Gal4) when GFP binds to its receptor, then the effector will activate the expression of BFP. Only receiver cells in direct contact with sender cells will be activated for BFP expression. (
B) Cell–cell contact mediated by artificial GFP gradient (refer to Section 4.1). The notch core will release the effector (shown as Gal4) only when free GFP binds to the anchor (shown as LaG2) of neighboring cells, which leads to the expression of mCherry. The activation of mCherry expression can be formed by a soluble GFP gradient (adapted from Morsut et al. [
5] and Toda et al. [
62]).
5. Other Useful Biological Parts and Circuits
5.1. For Prokaryotes
5.1.1. SigI-RsgI Cell–cell Contact Signaling
The SigI-RsgI pathway is currently the only known signaling pathway in prokaryotes that transduces signals through the cell membrane via autoproteolysis [
67], resembling the Delta-Notch signaling mechanism observed in eukaryotes. Given its ability to facilitate cell–cell contact signaling in bacteria, the SigI-RsgI pathway holds great potential as a valuable circuit for patterning.
Initially discovered in
Clostridium thermocellum [
68], the mechanism of the SigI-RsgI signaling has been recently elucidated. RsgI possesses an autoproteolytic activity within its periplasmic domain (PD) structure [
6]. The auto-cleavage of the β fragment results in the release of the N-terminal domain (NTD). Subsequently, the NTD is degraded by ClpXP, leading to the liberation and activation of the SigI protein, which was initially inhibited by the NTD. In its natural context, SigI activates the expression of cellulosomal genes (depicted in ).
. The structure of RsgI, and the model of RsgI self-cleavage and signal transduction [
6]. The binding of substrate to CBM/GH triggers the self-cleavage of PD-β1 in RsgI, which leads to the cleavage of NTD and release of SigI which affects the expression of the downstream target gene (adapted from Chen et al. [
6]).
As the SigI-RsgI pathway shares similarities with the Delta-Notch signaling mechanism in eukaryotes, it presents an opportunity for researchers to explore cell–cell contact signaling in prokaryotes. The study of this pathway could provide valuable insights into the evolution of cell–cell signaling mechanisms and the role of such pathways in cellular communication and tissue patterning. Additionally, understanding the SigI-RsgI pathway may lead to new strategies for engineering synthetic circuits in prokaryotes, with potential applications in biotechnology, environmental remediation, and bioenergy production.
5.1.2. MinDEC System to Control Cell Division
The MinDEC protein system is a widely studied example of gradient formation in
E. coli. In vitro experiments have demonstrated that the MinDEC system is capable of generating oscillatory patterns [
69]. In vivo, this system regulates the positioning of the Z-ring during cell division in bacteria. It involves the proteins MinE and MinD, which form a gradient to guide the proper placement of the Z-ring [
70]. Importantly, it has been found that the presence of MinC is not necessary for the formation of the MinDE gradient [
71].
The MinD protein binds to ATP and the cytoplasmic membrane, where it forms a complex with MinC, an inhibitor of FtsZ polymerization. MinE stimulates the ATPase activity of MinD, causing it to release MinC and the membrane (depicted in ). This process leads to the formation of a MinDE gradient, which oscillates between the poles of the cell.
The oscillatory behavior of the MinDE gradient ensures that the Z-ring, composed of FtsZ proteins, forms at the midcell, where the concentration of MinC is the lowest. The proper positioning of the Z-ring is crucial for accurate cell division and the generation of two identical daughter cells.
. The mechanism of MinDE gradient formation [
70]. MinD and MinE achieve dynamic association and dissociation through ATP phosphorylation and dimerization, thereby causing oscillations (adapted from Ramm et al. [
70]).
Several studies have explored the manipulation of bacterial cell division to achieve pattern formation. Duran-Nebreda et al. successfully realized a periodic symmetry-breaking pattern by combining cell division control with quorum sensing. They utilized the MinC gene, an AHL quorum-sensing circuit, and the JunA gene, which regulates cell adhesion, to achieve this outcome [
7]. These findings suggest that the unequal cell division controlled by the MinDE system could potentially give rise to symmetry-breaking patterns in bacterial colonies. The study by Duran-Nebreda et al. highlights the potential of integrating multiple cellular processes, such as cell division, quorum sensing, and cell adhesion, to generate complex patterns in bacterial populations. By exploiting the MinDE system’s role in controlling cell division and combining it with other genetic circuits, researchers can create bacterial strains with specific patterning properties.
5.1.3. Orthogonal Quorum-sensing Circuits
In addition to AHL (acyl-homoserine lactone) quorum sensing, bacteria commonly employ quorum sensing mechanisms mediated by long-range diffusing small molecules. These molecules facilitate communication among bacterial cells, allowing them to coordinate their behavior and respond to changes in population density. Consequently, there exists a wide range of synthetase and receptor pairs that can be combined with AHL circuits, thereby enabling the design of more intricate and complex signaling networks. Some examples of these small molecules and their corresponding synthetase-signal molecule-receptor sets are listed in .
By harnessing the diversity of quorum sensing mechanisms and incorporating them into synthetic gene circuits, researchers can design more sophisticated bacterial communication networks. These engineered networks can be utilized to investigate complex biological processes, create advanced microbial consortia, and develop novel therapeutic strategies. Moreover, the integration of multiple quorum sensing pathways can facilitate the construction of multilayered, hierarchical signaling systems that more closely mimic the complexity of natural systems.
. Quorum-sensing circuits in bacteria (adapted from Papenfort and Bassler [
72]).
The orthogonality of quorum-sensing circuits based on homoserine lactone (HSL) molecules has been a subject of investigation. Studies have shown that LuxR and LasR receptors exhibit responsiveness to various HSL molecules, whereas the BjaR receptor demonstrates a relatively higher degree of orthogonality compared to other HSL quorum-sensing circuits [
78]. This orthogonality property allows for the independent and specific control of different quorum sensing circuits, facilitating the construction of more tailored and versatile synthetic biological systems.
Orthogonality is a crucial aspect when designing synthetic biological systems, as it enables the coexistence of multiple genetic circuits within the same cell or population without interfering with each other’s function. By identifying and utilizing orthogonal receptors and HSL molecules, researchers can create more complex and sophisticated genetic circuits that can be independently controlled.
For example, orthogonal quorum sensing systems can be used to create multi-layered regulatory networks where the activation of one circuit depends on the output of another. This can lead to the development of more advanced synthetic biology applications, such as microbial consortia that perform multiple tasks in a coordinated manner or engineered bacteria that can respond to specific combinations of environmental cues [
79].
Furthermore, the identification and characterization of orthogonal quorum sensing systems can improve our understanding of how natural bacterial populations maintain the specificity of their communication channels despite the presence of numerous signaling molecules in their environment. This knowledge can be applied to the development of novel antimicrobial agents that target specific quorum sensing pathways, as well as strategies to mitigate the spread of antibiotic resistance and virulence factors in bacterial populations.
5.2. For Eukaryotes
5.2.1. Auxin Quorum-sensing Circuit
In the recent publication by Ma et al. in 2022, an artificial quorum-sensing signaling system based on auxin was introduced. Auxin, a plant hormone, serves as the signaling molecule that communicates the cell population state in this circuit. The receiver cell detects the presence of auxin in its environment, and upon binding of auxin to the auxin-inducible degron (AID) and osmotic stress-induced receptor 1 (osTIR1), it triggers the assembly of the SCF (Skp1-Cullin-F-box) complex. This complex, in turn, induces the degradation of the target protein BlastR (depicted in ) [
8].
This innovative approach demonstrates the potential for employing non-traditional signaling molecules, such as auxin, in designing synthetic quorum-sensing circuits. By utilizing auxin, which is not native to bacterial communication systems, the authors were able to create a signaling pathway that is orthogonal to endogenous bacterial quorum-sensing systems. This allows for more precise control and manipulation of the engineered circuit without interference from native cellular processes.
The auxin-based quorum-sensing system developed by Ma et al. can serve as a foundation for further exploration of alternative signaling molecules and their potential applications in synthetic biology. The incorporation of non-native signaling molecules can expand the toolbox for designing more complex and sophisticated genetic circuits, enabling the development of engineered bacteria with novel functions and capabilities. Additionally, the study highlights the potential for cross-disciplinary research, as it demonstrates the successful integration of a plant hormone into a bacterial communication system.
. The artificial auxin quorum sensing circuit in mammalian cell. The concentration of auxin or auxin precursor regulates the survival of cell by binding to AID and osTIR1, which causes the degradation of BlastR via ubiquitination (adapted from Ma et al. [
8]).
Auxin is known for its high diffusion coefficient, which poses challenges for creating spatial patterns in liquid mammalian cell culture mediums. However, the study by Ma et al. demonstrates that auxin can form a gradient in low-melting-point agarose, thus enabling the patterning of cells cultured within similar hydrogels [
8].
The ability to create spatial patterns and gradients using auxin in hydrogels opens up new opportunities for tissue engineering and regenerative medicine applications. By embedding cells within hydrogels and exposing them to auxin gradients, researchers can control the spatial organization and differentiation of cells, potentially leading to the formation of complex, multi-cellular structures that mimic native tissues.
Furthermore, the use of auxin gradients in hydrogels can also be applied to study cell migration, chemotaxis, and cellular responses to environmental cues. Such investigations can provide insights into the mechanisms underlying tissue development, wound healing, and disease progression in more complex, multicellular systems.
Overall, the findings by Ma et al. not only demonstrate the potential of using non-traditional signaling molecules like auxin in synthetic biology but also reveal new avenues for exploring spatial patterning and organization in mammalian cell culture systems using hydrogels and other similar materials.
5.2.2. Diffusible RNA Exporter
Horns et al., in their recent study, presented an artificial RNA exporter system capable of facilitating cell–cell RNA delivery. This system involves the assembly of RNA-binding proteins, self-assembling capsids, fusogens, and RNA cargo labeled with an export tag. The modular nature of the RNA exporter system, known as COURIERs (Communication Using RNA Import-Export Relays), allows for the potential delivery of customized mRNA signals within a cell population [
80].
The study demonstrated the feasibility of cell–cell RNA delivery using the diffusible RNA exporter system. However, it is important to note that the diffusion coefficient of the specific RNA exporter used in the study (EPN24-MCP) was not measured. Additionally, the ability of the RNA exporter to diffuse within a hydrogel environment remains unknown. Further research is needed to investigate these aspects and determine the diffusion properties of the RNA exporter under different conditions.
Understanding the diffusion properties of the RNA exporter system will be crucial for its application in synthetic biology and tissue engineering. The ability to control the diffusion and spatial distribution of RNA signals could enable the creation of more complex and dynamic cellular communication networks, as well as the development of novel therapeutic strategies for targeted gene delivery and regulation.
Furthermore, exploring the compatibility of the RNA exporter system with different hydrogel environments could provide valuable insights into its potential use in three-dimensional (3D) cell culture systems and tissue engineering applications. By combining the RNA exporter system with hydrogel-based cell culture platforms, researchers may be able to design more sophisticated and controlled multicellular systems that mimic native tissue structures and functions.
5.3. Subcellular Regulation
Synthetic Biomolecular Condensates
Pattern formation in biological systems often involves changes in gene expression levels within individual cells. Therefore, incorporating bioparts related to subcellular regulation can be valuable for designing pattern formation networks. Synthetic biomolecular condensates, which are artificially designed bioparts, offer a means to introduce symmetry breaking within cells [
9].
The synthetic condensate protein module consists of three essential components. First, a synthetic intrinsically disordered protein (synIDP), which is a resilin-like polypeptide (RLP), acts as a zwitterionic domain to drive the condensation process. Second, a helix-turn-helix DNA-binding domain (DBD) derived from the ParB-parS system [
81] enables specific DNA sequence binding. Lastly, a C-terminal dimerization domain (DD) enhances phase separation coupled with percolation. Phase separation occurs only when the DBD binds to its target DNA sequence, resulting in the encapsulation of the plasmid within the protein condensate (depicted in ). This can lead to plasmid sequestration or transcriptional regulation [
9].
By integrating these synthetic biomolecular condensates into cellular systems, it becomes possible to introduce spatial organization and symmetry-breaking effects, enabling the design of pattern formation networks with precise control over gene expression and cellular behavior. These condensates can be used to create localized regions within cells where specific biochemical reactions or processes occur, mimicking the compartmentalization found in natural biological systems. This enables the fine-tuning of cellular processes, such as signal transduction, gene expression, and protein synthesis, in response to external or internal stimuli.
Additionally, the use of synthetic biomolecular condensates can provide new opportunities for studying the principles of pattern formation and self-organization in living systems. Understanding the mechanisms that govern these processes can lead to the development of more advanced synthetic biology tools and applications, including tissue engineering, regenerative medicine, and the creation of artificial life forms. Moreover, the ability to manipulate subcellular organization using biomolecular condensates can also enhance our understanding of cellular processes and contribute to the development of novel therapeutic strategies for treating diseases related to cellular dysfunction.
. The structure and mechanism of synthetic biomolecular condensates. The structure of synIDP-DBD-DD binds to target sequence of plasmids while driving the phase transition process, thereby causing the encapsulation of the plasmids in the protein condensate (adapted from Dai et al. [
9]).
6. Conclusions
In conclusion, advancements in biology and computer science from the 1950s to the 21st century have deepened our understanding of multicellular organism development, inspiring a wide range of synthetic biology tools. Genetically engineered circuits are now capable of mimicking many naturally occurring forms of self-organization, aligning with the idea expressed by Michael Elowitz and Wendell A. Lim: “build life to understand it” [
18].
With the aid of physical models and synthetic biology tools, it is now possible to design and realize more intricate and complex patterns in both eukaryotic and prokaryotic systems. However, creating functional patterning circuits or networks in the wet lab is still challenging due to the numerous parameters involved and the difficulty in adjusting them.
To overcome these challenges, the strategy for designing circuits or networks may need improvement. Using numerical simulations to assist wet lab experiments can help reduce the need for extensive parameter adjustments of biological parts and circuits. For different patterning goals, selecting a network capable of forming the desired pattern in silico and then choosing suitable bioparts based on the required parameter range of the network is a more efficient approach.
To implement this process, it is crucial to measure the parameters of existing bioparts and their interactions with each other, necessitating the establishment of a comprehensive biopart library [
82]. While there are already biopart databases integrating information from various biopart libraries worldwide, they do not typically include reaction parameters of bioparts. Integrating the reaction parameters of existing bioparts into these databases would greatly facilitate the modular design of patterning networks and other genetic circuits. This will ultimately advance the field of synthetic biology and help pave the way for more complex and sophisticated applications in areas such as tissue engineering, regenerative medicine, and the creation of artificial life forms.
Acknowledgments
J.-D.H. thanks the L & T Charitable Foundation for their support. We thank the American Association for the Advancement of Science for granting permission to adapt and include their figures in this review article.
Author Contributions
Methodology, A.X.; Writing – Original Draft Preparation, A.X.; Writing – Review & Editing, L.L. and J.-D.H.; Supervision, J-D.H.; Funding Acquisition, J.-D.H.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
The work was supported by the National Key Research and Development Program of China (2021YFA0910700) to J.-D.H.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1.
Turing AM. The Chemical Basis of Morphogenesis.
Philos. Trans.R. Soc. Lond. B Biol. Sci. 1952,
237, 37–72.
[Google Scholar]
2.
Warmflash A, Sorre B, Etoc F, Siggia ED, Brivanlou AH. A method to recapitulate early embryonic spatial patterning in human embryonic stem cells.
Nat. Method. 2014,
11, 847–854.
[Google Scholar]
3.
Harrison SE, Sozen B, Christodoulou N, Kyprianou C, Zernicka-Goetz M. Assembly of embryonic and extraembryonic stem cells to mimic embryogenesis in vitro.
Science 2017,
356, eaal1810.
[Google Scholar]
4.
Liu C, Fu X, Liu L, Ren X, Chau CK, Li S, et al. Sequential establishment of stripe patterns in an expanding cell population.
Science 2011,
334, 238–241.
[Google Scholar]
5.
Morsut L, Roybal KT, Xiong X, Gordley RM, Coyle SM, Thomson M, et al. Engineering Customized Cell Sensing and Response Behaviors Using Synthetic Notch Receptors.
Cell 2016,
164, 780–791.
[Google Scholar]
6.
Chen C, Dong S, Yu Z, Qiao Y, Li J, Ding X, et al. Essential autoproteolysis of bacterial anti-σ factor RsgI for transmembrane signal transduction.
Sci. Adv. 2023,
9, eadg4846.
[Google Scholar]
7.
Duran-Nebreda S, Pla J, Vidiella B, Piñero J, Conde-Pueyo N, Solé R. Synthetic Lateral Inhibition in Periodic Pattern Forming Microbial Colonies.
ACS Synth. Biol. 2021,
10, 277–285.
[Google Scholar]
8.
Ma Y, Budde MW, Mayalu MN, Zhu J, Lu AC, Murray RM, et al. Synthetic mammalian signaling circuits for robust cell population control.
Cell 2022,
185, 967–979.e12.
[Google Scholar]
9.
Dai Y, Farag M, Lee D, Zeng X, Kim K, Son HI, et al. Programmable synthetic biomolecular condensates for cellular control.
Nat. Chem. Biol. 2023,
19, 518–528.
[Google Scholar]
10.
Xu X, Risoul V, Byrne D, Champ S, Douzi B, Latifi A. HetL, HetR and PatS form a reaction-diffusion system to control pattern formation in the cyanobacterium nostoc PCC 7120.
Elife 2020,
9, e59190.
[Google Scholar]
11.
Glover JD, Sudderick ZR, Shih BB-J, Batho-Samblas C, Charlton L, Krause AL, et al. The developmental basis of fingerprint pattern formation and variation.
Cell 2023,
186, 940–956.
[Google Scholar]
12.
Kaelin CB, McGowan KA, Barsh GS. Developmental genetics of color pattern establishment in cats.
Nat. Commun. 2021,
12, 5127.
[Google Scholar]
13.
Sick S, Reinker S, Timmer J, Schlake T. WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism.
Science 2006,
314, 1447–1450.
[Google Scholar]
14.
Economou AD, Ohazama A, Porntaveetus T, Sharpe PT, Kondo S, Basson MA, et al. Periodic stripe formation by a Turing mechanism operating at growth zones in the mammalian palate.
Nat. Genet. 2012,
44, 348–351.
[Google Scholar]
15.
Schiffmann Y. Turing-Child field underlies spatial periodicity in Drosophila and planarians.
Progr. Biophys. Mol. Biol. 2011,
105, 258–269.
[Google Scholar]
16.
Levin SA, Segel LA. Hypothesis for origin of planktonic patchiness.
Nature 1976,
259, 659.
[Google Scholar]
17.
Mimura M, Murray JD. On a diffusive prey-predator model which exhibits patchiness.
J. Theor. Biol. 1978,
75, 249–262.
[Google Scholar]
18.
Elowitz M, Lim WA. Build life to understand it.
Nature 2010,
468, 889–890.
[Google Scholar]
19.
Tanaka M, Montgomery SM, Yue L, Wei Y, Song Y, Nomura T, et al. Turing pattern-based design and fabrication of inflatable shape-morphing structures.
Sci. Adv. 2023,
9, eade4381.
[Google Scholar]
20.
Vittadello ST, Leyshon T, Schnoerr D, Stumpf MPH. Turing pattern design principles and their robustness.
Philos. Trans. A Math. Phys. Eng. Sci. 2021,
379, 20200272.
[Google Scholar]
21.
Entchev EV, Schwabedissen A, González-Gaitán M. Gradient formation of the TGF-beta homolog Dpp.
Cell 2000,
103, 981–992.
[Google Scholar]
22.
Lecuit T, Brook WJ, Ng M, Calleja M, Sun H, Cohen SM. Two distinct mechanisms for long-range patterning by Decapentaplegic in the Drosophila wing.
Nature 1996,
381, 387–393.
[Google Scholar]
23.
Inomata H. Scaling of pattern formations and morphogen gradients.
Dev. Growth Differ. 2017,
59, 41–51.
[Google Scholar]
24.
Szurmant H, Ordal GW. Diversity in chemotaxis mechanisms among the bacteria and archaea.
Microbiol. Mol. Biol. Rev. 2004,
68, 301–319.
[Google Scholar]
25.
Budrene EO, Berg HC. Dynamics of formation of symmetrical patterns by chemotactic bacteria.
Nature 1995,
376, 49–53.
[Google Scholar]
26.
Fitzhugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane.
Biophys. J. 1961,
1, 445–466.
[Google Scholar]
27.
Nagumo J, Arimoto S, Yoshizawa S. An Active Pulse Transmission Line Simulating Nerve Axon.
Proc. IRE 1962,
50, 2061–2070.
[Google Scholar]
28.
Meinhardt H, Gierer A. Pattern formation by local self-activation and lateral inhibition.
Bioessays 2000,
22, 753–760.
[Google Scholar]
29.
Zheng MM, Shao B, Ouyang Q. Identifying network topologies that can generate turing pattern.
J. Theor. Biol. 2016,
408, 88–96.
[Google Scholar]
30.
Dexter JS. The Analysis of a Case of Continuous Variation in Drosophila by a Study of Its Linkage Relations.
Am. Nat. 1914,
48, 712–758.
[Google Scholar]
31.
Logeat F, Bessia C, Brou C, LeBail O, Jarriault S, Seidah NG, et al. The Notch1 receptor is cleaved constitutively by a furin-like convertase.
Proc. Natl. Acad. Sci. USA 1998,
95, 8108–8112.
[Google Scholar]
32.
Wang W. Struhl G. Drosophila Epsin mediates a select endocytic pathway that DSL ligands must enter to activate Notch.
Development 2004,
131, 5367–5380.
[Google Scholar]
33.
van den Brink SC, Baillie-Johnson P, Balayo T, Hadjantonakis AK, Nowotschin S, Turner DA, et al. Symmetry breaking, germ layer specification and axial organisation in aggregates of mouse embryonic stem cells.
Development 2014,
141, 4231–4242.
[Google Scholar]
34.
Rivron NC, Frias-Aldeguer J, Vrij EJ, Boisset JC, Korving J, Vivié J, et al. Blastocyst-like structures generated solely from stem cells.
Nature 2018,
557, 106–111.
[Google Scholar]
35.
Rossant J, Tam PPL. Opportunities and challenges with stem cell-based embryo models.
Stem Cell Rep. 2021,
16, 1031–1038.
[Google Scholar]
36.
Bao M, Cornwall-Scoones J, Zernicka-Goetz M. Stem-cell-based human and mouse embryo models.
Curr. Opin. Genet. Dev. 2022,
76, 101970.
[Google Scholar]
37.
Lee HC, Hastings C, Oliveira NMM, Pérez-Carrasco R, Page KM, Wolpert L, et al. ‘Neighbourhood watch’ model: embryonic epiblast cells assess positional information in relation to their neighbours.
Development 2022,
149, dev200295.
[Google Scholar]
38.
Wolpert L. Positional information and the spatial pattern of cellular differentiation.
J. Theor. Biol. 1969,
25, 1–47.
[Google Scholar]
39.
Heemskerk I, Warmflash A. Pluripotent stem cells as a model for embryonic patterning: From signaling dynamics to spatial organization in a dish.
Dev. Dyn. 2016,
245, 976–990.
[Google Scholar]
40.
Liu L, Oura S, Markham Z, Hamilton JN, Skory RM, Li L, et al. Modeling post-implantation stages of human development into early organogenesis with stem-cell-derived peri-gastruloids.
Cell 2023,
186, 3776–3792.
[Google Scholar]
41.
Weatherbee BAT, Gantner CW, Iwamoto-Stohl LK, Daza RM, Hamazaki N, Shendure J, et al. Pluripotent stem cell-derived model of the post-implantation human embryo.
Nature 2023,
622, 584–593.
[Google Scholar]
42.
Pedroza M, Gassaloglu SI, Dias N, Zhong L, Hou TJ, Kretzmer H, et al. Self-patterning of human stem cells into post-implantation lineages.
Nature 2023,
622, 574–583.
[Google Scholar]
43.
Ai Z, Niu B, Yin Y, Xiang L, Shi G, Duan K, et al. Dissecting peri-implantation development using cultured human embryos and embryo-like assembloids.
Cell Res. 2023,
33, 661–678.
[Google Scholar]
44.
Hislop J, Alavi A, Song Q, Schoenberger R, Kamyar KF, LeGraw R, et al. Modelling Human Post-Implantation Development via Extra-Embryonic Niche Engineering. bioRxiv 2023, doi:10.1101/2023.06.15.545118.
45.
Oldak B, Wildschutz E, Bondarenko V, Comar MY, Zhao C, Aguilera-Castrejon A, et al. Complete human day 14 post-implantation embryo models from naive ES cells.
Nature 2023,
622, 562–573.
[Google Scholar]
46.
Yuan G, Wang J, Liu Z, Chen M, Zhu P, Zhang H, et al. Establishment of a novel non-integrated human pluripotent stem cell-based gastruloid model. bioRxiv 2023, doi:10.1101/2023.06.28.546720.
47.
Yu L, Wei Y, Duan J, Schmitz DA, Sakurai M, Wang L, et al. Blastocyst-like structures generated from human pluripotent stem cells.
Nature 2021,
591, 620–626.
[Google Scholar]
48.
Liu, X., Pan JP, Schröder J, Aberkane A, Ouyang JF, Mohenska M, et al. Modelling human blastocysts by reprogramming fibroblasts into iBlastoids.
Nature 2021,
591, 627–632.
[Google Scholar]
49.
Kagawa H, Javali A, Khoei HH, Sommer TM, Sestini G, Novatchkova M, et al. Human blastoids model blastocyst development and implantation.
Nature 2022,
601, 600–605.
[Google Scholar]
50.
Landecker HL, Clark AT. Human embryo models made from pluripotent stem cells are not synthetic; they aren’t embryos, either.
Cell Stem Cell 2023,
30, 1290–1293.
[Google Scholar]
51.
Pinzón-Arteaga CA, Wang Y, Wei Y, Ribeiro Orsi AE, Li L, Scatolin G, et al. Bovine blastocyst-like structures derived from stem cell cultures.
Cell Stem Cell 2023,
30, 611–616.
[Google Scholar]
52.
Li J, Zhu Q, Cao J, Liu Y, Lu Y, Sun Y, et al. Cynomolgus monkey embryo model captures gastrulation and early pregnancy.
Cell Stem Cell 2023,
30, 362–377.
[Google Scholar]
53.
Oh SY, Na SB, Kang YK, Do JT. In Vitro Embryogenesis and Gastrulation Using Stem Cells in Mice and Humans.
Int. J. Mol. Sci. 2023,
24, 13655.
[Google Scholar]
54.
Fan Y, Min Z, Alsolami S, Ma Z, Zhang E, Chen W, et al. Generation of human blastocyst-like structures from pluripotent stem cells.
Cell Discov. 2021,
7, 81.
[Google Scholar]
55.
Tu Z, Bi Y, Zhu X, Liu W, Hu J, Wu L, et al. Modeling human pregastrulation development by 3D culture of blastoids generated from primed-to-naïve transitioning intermediates.
Protein Cell 2023,
14, 337–349.
[Google Scholar]
56.
Zhang S, Chen T, Chen N, Gao D, Shi B, Kong S, et al. Implantation initiation of self-assembled embryo-like structures generated using three types of mouse blastocyst-derived stem cells.
Nat. Commun. 2019,
10, 496.
[Google Scholar]
57.
Sozen B, Amadei G, Cox A, Wang R, Na E, Czukiewska S, et al. Self-assembly of embryonic and two extra-embryonic stem cell types into gastrulating embryo-like structures.
Nat. Cell Biol. 2018,
20, 979–989.
[Google Scholar]
58.
Lau KYC, Rubinstein H, Gantner CW, Hadas R, Amadei G, Stelzer Y, et al. Mouse embryo model derived exclusively from embryonic stem cells undergoes neurulation and heart development.
Cell Stem Cell 2022,
29, 1445–1458.e8.
[Google Scholar]
59.
Tarazi S, Aguilera-Castrejon A, Joubran C, Ghanem N, Ashouokhi S, Roncato F, et al. Post-gastrulation synthetic embryos generated ex utero from mouse naive ESCs.
Cell 2022,
185, 3290–3306.e25.
[Google Scholar]
60.
Xu Y, Zhao J, Ren Y, Wang X, Lyu Y, Xie B, et al. Derivation of totipotent-like stem cells with blastocyst-like structure forming potential.
Cell Res. 2022,
32, 513–529.
[Google Scholar]
61.
Stapornwongkul KS, de Gennes M, Cocconi L, Salbreux G, Vincent JP. Patterning and growth control in vivo by an engineered GFP gradient.
Science 2020,
370, 321–327.
[Google Scholar]
62.
Toda S, McKeithan WL, Hakkinen TJ, Lopez P, Klein OD, Lim WA. Engineering synthetic morphogen systems that can program multicellular patterning.
Science 2020,
370, 327–331.
[Google Scholar]
63.
Li S, Wu S, Ren Y, Meng Q, Yin J, Yu Z. Characterization of differentiated autoregulation of LuxI/LuxR-type quorum sensing system in
Pseudoalteromonas.
Biochem. Biophys. Res. Commun. 2022,
590, 177–183.
[Google Scholar]
64.
Wolfe AJ, Berg HC. Migration of bacteria in semisolid agar.
Proc. Natl. Acad. Sci. USA 1989,
86, 6973–6977.
[Google Scholar]
65.
Vanag VK, Epstein IR. Cross-diffusion and pattern formation in reaction-diffusion systems.
Phys. Chem. Chem. Phys. 2009,
11, 897–912.
[Google Scholar]
66.
Micchelli CA, Rulifson EJ, Blair SS. The function and regulation of cut expression on the wing margin of Drosophila: Notch, Wingless and a dominant negative role for Delta and Serrate.
Development 1997,
124, 1485–1495.
[Google Scholar]
67.
Bastiaansen KC, Otero-Asman JR, Luirink J, Bitter W, Llamas MA. Processing of cell-surface signalling anti-sigma factors prior to signal recognition is a conserved autoproteolytic mechanism that produces two functional domains.
Environ. Microbiol. 2015,
17, 3263–3277.
[Google Scholar]
68.
Kahel-Raifer H, Jindou S, Bahari L, Nataf Y, Shoham Y, Bayer EA, et al. The unique set of putative membrane-associated anti-sigma factors in Clostridium thermocellum suggests a novel extracellular carbohydrate-sensing mechanism involved in gene regulation.
FEMS Microbiol. Lett. 2010,
308, 84–93.
[Google Scholar]
69.
Vecchiarelli AG, Li M, Mizuuchi M, Hwang LC, Seol Y, Neuman KC, et al. Membrane-bound MinDE complex acts as a toggle switch that drives Min oscillation coupled to cytoplasmic depletion of MinD.
Proc. Natl. Acad. Sci. USA 2016,
113, 1479–1488.
[Google Scholar]
70.
Ramm B, Heermann T, Schwille P. The
E. coli MinCDE system in the regulation of protein patterns and gradients.
Cell. Mol. Life Sci. 2019,
76, 4245–4273.
[Google Scholar]
71.
Godino E, Doerr A, Danelon C. Min waves without MinC can pattern FtsA-anchored FtsZ filaments on model membranes.
Commun. Biol. 2022,
5, 675.
[Google Scholar]
72.
Papenfort K, and Bassler BL. Quorum sensing signal-response systems in Gram-negative bacteria.
Nat. Rev. Microbiol. 2016,
14, 576–588.
[Google Scholar]
73.
Mukherjee S, Moustafa D, Smith CD, Goldberg JB, Bassler BL. The RhlR quorum-sensing receptor controls Pseudomonas aeruginosa pathogenesis and biofilm development independently of its canonical homoserine lactone autoinducer.
PLoS Pathog. 2017,
13, e1006504.
[Google Scholar]
74.
Swem LR, Swem DL, O’Loughlin CT, Gatmaitan R, Zhao B, Ulrich SM, et al. A quorum-sensing antagonist targets both membrane-bound and cytoplasmic receptors and controls bacterial pathogenicity.
Mol. Cell 2009,
35, 143–153.
[Google Scholar]
75.
Building light-activated synthetic cells that induce gene expression in bacteria via quorum sensing.
Nat. Chem. Biol. 2023,
19, 1052–1053.
[Google Scholar]
76.
Ahlgren NA, Harwood CS, Schaefer AL, Giraud E, Greenberg EP. Aryl-homoserine lactone quorum sensing in stem-nodulating photosynthetic bradyrhizobia.
Proc. Natl. Acad. Sci. USA 2011,
108, 7183–7188.
[Google Scholar]
77.
Hirakawa H, Oda Y, Phattarasukol S, Armour CD, Castle JC, Raymond CK, et al. Activity of the Rhodopseudomonas palustris p-coumaroyl-homoserine lactone-responsive transcription factor RpaR.
J. Bacteriol. 2011,
193, 2598–2607.
[Google Scholar]
78.
Tekel SJ, Smith CL, Lopez B, Mani A, Connot C, Livingstone X, et al. Engineered Orthogonal Quorum Sensing Systems for Synthetic Gene Regulation in Escherichia coli.
Front. Bioeng. Biotechnol. 2019,
7, 80.
[Google Scholar]
79.
Brödel AK, Jaramillo A, Isalan M. Engineering orthogonal dual transcription factors for multi-input synthetic promoters.
Nat. Commun. 2016,
7, 13858.
[Google Scholar]
80.
Horns F, Martinez JA, Fan C, Haque M, Linton JM, Tobin V, et al. Engineering RNA export for measurement and manipulation of living cells.
Cell 2023,
186, 3642–3658.e32.
[Google Scholar]
81.
Livny J, Yamaichi Y, Waldor MK. Distribution of centromere-like parS sites in bacteria: insights from comparative genomics.
J. Bacteriol. 2007,
189, 8693–8703.
[Google Scholar]
82.
Plahar HA, Rich TN, Lane SD, Morrell WC, Leanne Springthorpe, Nnadi O, et al. BioParts—Biological Parts Search Portal and Updates to the ICE Parts Registry Software Platform.
ACS Synth. Biol. 2021,
10, 2649–2660.
[Google Scholar]