Effects of Changing the Specific Surface Area in the Ceramic Matrix of CAC-Containing Refractory Castables on the Rheology and Processing
Received: 01 September 2025 Revised: 15 September 2025 Accepted: 03 November 2025 Published: 18 November 2025
© 2025 The authors. This is an open access article under the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/).
1. Introduction
1.1. Composition of Refractory Castables
Refractory castables are extensively employed in high-temperature applications because they combine superior thermal resistance and mechanical strength with faster, more cost-effective, and energy-efficient installation compared to conventional bricklaying. Their composition typically includes a coarse and medium fraction (aggregates, often up to 6 mm, but coarser grains of approximately 15 mm can also be used) and a fine matrix containing particles below 45 μm. The particle size distribution follows multimodal packing models in which fine particles efficiently occupy the interstitial voids between coarser grains. This optimised packing strategy increases bulk density and minimizes porosity [1,2,3,4,5]. Recent developments in the production of denser refractory castables have focused on further refining raw materials, with current d50 values of approximately 0.5 μm [6]. Silica sol-bonded systems can incorporate even finer particles, reaching minimum particle sizes of about 15 nm. The use of highly sintered and (very) finely milled alumina raw materials significantly increases the specific surface area of the ceramic matrix of refractory castables. Such refinements not only reduce porosity but also influence rheological behaviour, setting kinetics, and sintering.
This article is part of a series of publications systematically investigating the influence of the specific surface area on the properties of refractory castables. While the first two studies focused on the effects of the specific surface area of the ceramic matrix on dispersion and mixing process [7], and on initial stiffening and setting [8], the present publication addresses the impact on rheology and processing. By expanding the scope to this important aspect, this study provides an essential complementary contribution to understanding the rheological behaviour and processing characteristics of refractory castables.
1.2. Dispersion of Refractory Castables
To ensure sufficient particle separation within the fine-grained matrix, dispersing agents are indispensable components of refractory castables [5,9]. These additives, composed of surface-active organic or inorganic molecules, act by overcoming interparticle forces and thereby control the rheological behaviour of the material. Typical systems include polycarboxylate ethers, acrylates, or polyphosphates, which adsorb onto particle surfaces and generate electrostatic, steric, or electrosteric repulsion, effectively preventing agglomeration [10]. The concentration of the dispersing agent employed can significantly influence various castable properties.
However, different dispersing agent systems act through distinct dispersion mechanisms. Certain compounds, such as polyphosphates or acrylates, can form sparingly soluble precipitates with Ca2+ ions (originating from CA-cement dissolution) once critical concentrations are exceeded, leading to a loss of workability and premature stiffening [11,12]. In contrast, polycarboxylate ethers with long side chains, for example, remain stable even at elevated Ca2+ levels and can therefore maintain dispersion and rheological stability until the hydration reduces the free water content below a critical value [11,12,13,14].
A more comprehensive description of the dispersion of refractory castables and the associated mechanisms is provided in Holleyn et al. [7,8].
1.3. Rheological Models
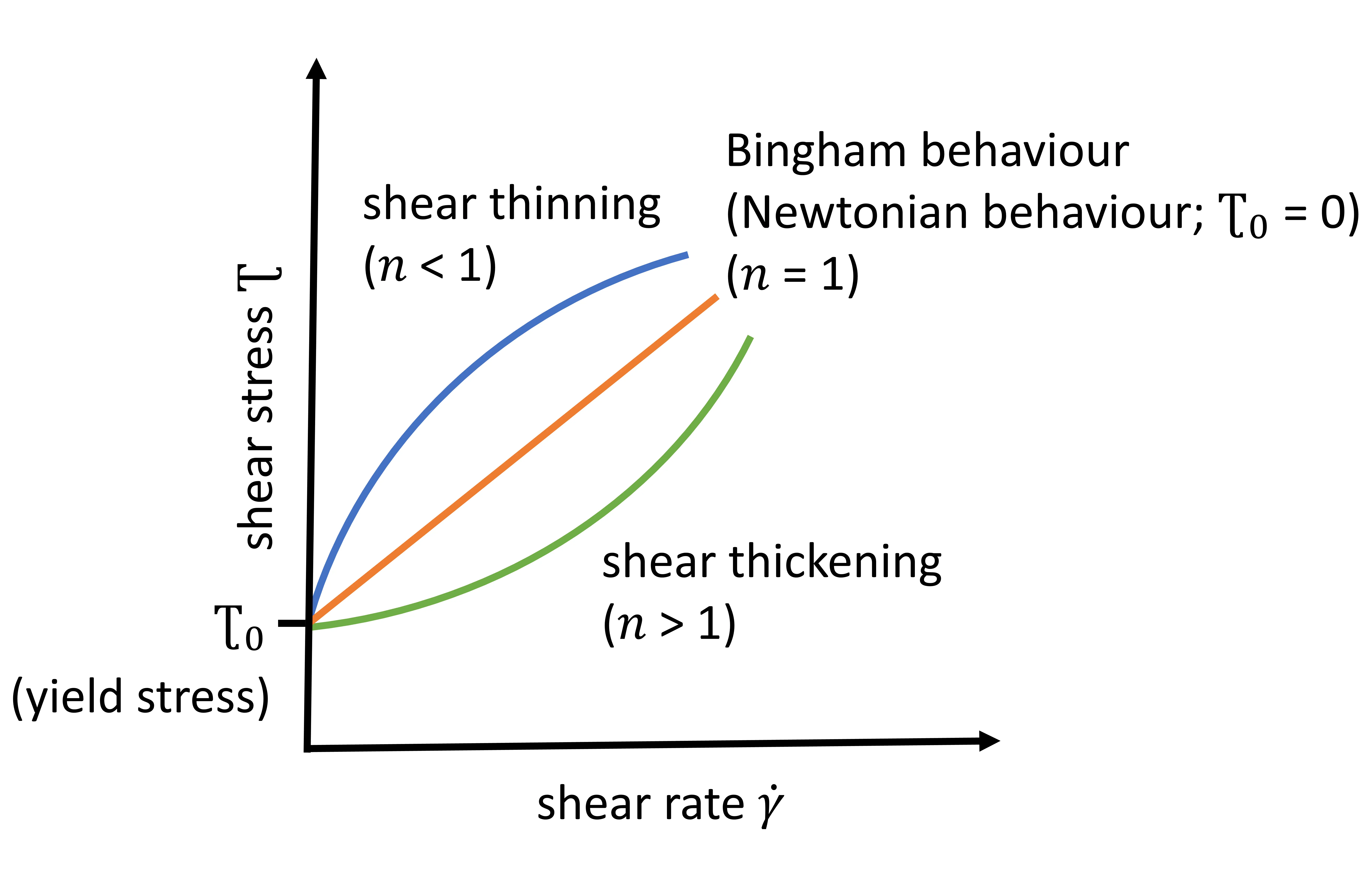
Various rheological models are employed to describe the rheological behaviour of coarse-grained dispersions, such as building materials and refractory castables. In particular, the Bingham (Equation (1)) and Herschel-Bulkley (Equation (2)) models play a central role [5,15,16,17,18,19,20,21]. Both models are based on the assumption that castables only begin to flow at a certain shear stress (the yield stress Ʈ0). The Bingham model describes a linear relationship between shear stress (Ʈ) and shear rate (γ̇) (Equation (1)), where ηBingh. represents the plastic viscosity according to Bingham. The Herschel-Bulkley model allows a non-linear description of this relationship (Equation (2)) and uses the parameters k (consistency, also known as relative viscosity) and n (flow index). This model is particularly suitable for materials that exhibit shear thinning behaviour (n < 1) or shear thickening behaviour (n > 1). When n = 1, the relationship is linear, as with the Bingham model, and the material exhibits Newtonian flow (if the condition Ʈ0 = 0 is given). If Ʈ0 ≠ 0, this rheological phenomenon is referred to as Bingham behaviour [5,15,16,17,18,19,20,21]. These relationships are illustrated in Figure 1.
|
```latexƮ= {Ʈ}_{0}+ {\eta }_{Bingh.} \stackrel{˙}{\gamma }``` |
(1) |
|
```latexƮ= {Ʈ}_{0}+k\mathrm{ }{\stackrel{˙}{\gamma }}^{n}``` |
(2) |
Rheometers are commonly used to characterise the rheological and flow properties of building materials and refractory castables. In building materials technology, however, the rheometers employed often have an undefined sheared surface or an unknown shear rate distribution in the testing device. Consequently, the shear rate cannot be determined precisely. Rheological models, such as the Bingham or Herschel-Bulkley model, can be applied to describe experimental data. Regression analysis of the measurement data allows the estimation of parameters such as yield stress and viscosity. The values obtained from such model fits must be regarded as relative rather than absolute physical quantities. They are suitable for comparative evaluation only under identical testing conditions, including the type and geometry of the measuring system, the measurement program, and the temperature [19,22]. Multi-point measurements at different shear rates can provide detailed flow curves and allow the derivation of relative yield stress and viscosity values, but the limitation to relative interpretation remains. An important factor influencing viscosity is the sample temperature. In most cases, viscosity decreases as the sample material heats up [18].
1.4. Rheology of Refractory Castables
Rheological properties play a critical role in determining the workability and compaction of refractory castables. Although the matrix composition predominantly determines the rheology of castables, the influence of the coarse grain fraction cannot be neglected. As particle size decreases, interparticle forces intensify, leading to increased viscosity. Bimodal and multimodal particle distributions of the ceramic matrix have proven effective in reducing viscosity, thereby improving flowability. In refractory castables, bimodal reactive aluminas are commonly used to optimise flow characteristics during moulding [6,9,23,24,25]. This approach can enhance flowability, increase packing density, and lower the energy demand during mixing.
However, controlling flow behaviour at high shear rates remains challenging, particularly in processes such as pumping. Shear thickening, characterised by a viscosity increase with rising shear rate, continues to be a critical issue. Empirical investigations on pumpable castables indicate that this phenomenon in industrial practice is often linked to insufficiently controlled matrix formulations [25]. Irregular surface geometries of coarse particles can further promote particle interlocking during flow, intensifying shear thickening behaviour [5].
When interpreting (dynamic) viscosity data, it is essential to consider the applied shear rate, since concentrated, particle-laden suspensions exhibit non-Newtonian behaviour.
Numerous models relate viscosity to solids content, with the Krieger-Dougherty equation being the most widely applied, capturing the increase of viscosity with solids volume fraction [5,9,15,16]. Mechanistically, higher particle packing restricts particle mobility and intensifies both interparticle forces and collision frequency, thereby increasing viscosity [9,25].
Beyond solids content, particle size and specific surface area significantly influence shear-dependent viscosity. At low solids content, the suspension exhibits close to Newtonian behaviour (over a wide shear rate range). Increasing solids loading promotes collisions at elevated shear rates, leading to shear thickening behaviour, while higher specific surface areas enhance shear thinning behaviour. This results in high viscosity at low shear rates and a pronounced decrease at higher shear. In practice, both effects can overlap, resulting in pseudo-Newtonian flow behaviour.
At a constant solids fraction, suspensions with smaller particles and ultrafine powders with an increased specific surface area exhibit elevated viscosity (due to stronger interparticle forces) at low shear rates [9]. This could be even more pronounced (in narrow particle size distributions) at high shear rates, because the probability of a particle collision increases again due to external forces [5,9].
A narrower particle size distribution leads to poorer packing efficiency. Consequently, more water is required during mixing to ensure sufficient workability or to reach the desired viscosity. In contrast, a broader and more optimised distribution improves packing density and increases the solids content, resulting in lower suspension viscosity and reduced water demand [5,9].
Literature reports a correlation between the rheology of matrix suspensions and the flow behaviour of concretes or refractory castables, suggesting that matrix rheology measurements can be used to qualitatively predict the rheological behaviour of the fully composed system [26,27,28,29,30,31]. Other studies, however, argue that the significant influence of aggregates makes matrix measurements alone insufficient for effectively describing the overall rheology of refractory castables [17,32].
As an indirect characterisation of the rheological behaviour of refractory castables and a prediction of the workability (processing), slump-flow tests are carried out as a standard to determine the spreading dimensions. According to the DIN EN ISO 1927-4 standard, slump-flow measurements are conducted by filling a slightly oiled conical mould placed on a plate. After the material is filled in, the mould is removed, and the spread of the material is measured manually to assess its consistency. While the primary purpose of the slump-flow test is to measure workability, it can also offer insights into other rheological properties, such as flow speed. Yet, the one-dimensional nature of the slump-flow test limits its ability to fully capture the complexity of the rheological behaviour of refractory castables [33]. Materials with the same yield stress but very different viscosities can lead to the same result when the spread is measured, even though their rheological behaviour during processing (e.g., pumping at high shear rates) is completely different. This could imply that castables may be entirely unsuitable for certain processing techniques, even if their slump-flow values appear appropriate [30,34]. To overcome these limitations, supplementary test methods with different setups have been explored. One example is the 3D slump-flow measurement, which provides a more comprehensive evaluation of the material’s performance [33,35]. This advanced technique employs imaging technology to capture the material’s spread pattern in three dimensions, offering more detailed insights into its flow properties.
The rheological behaviour of refractory castables can be investigated directly using building material rheometers. In these cases, regression of the measurement data can be performed using rheological models (see Section 1.3).
2. Materials and Methods
2.1. Experimental Materials
2.1.1. Refractory Castable Compositions and Their Preparation
Six systematically modified, self-flowing, high-alumina model refractory castables based on CA-cement (Secar 71, Imerys S.A., Paris, France) were investigated. The maximum grain size of the aggregates was 6 mm. All Al2O3 raw materials were supplied by Almatis GmbH, Ludwigshafen, Germany. The matrix fractions of the castables contained highly sintered and (very) finely milled Al2O3 raw materials with high specific surface areas. The particle size (-distribution) and the specific surface area were determined by measurements conducted in preliminary investigations [7,8].
Reactive aluminas, RG4000 (BET: 6.9 m2/g, d50: 0.54 µm); CTC20 (BET: 1.6 m2/g, d50: 1.80 µm); and a fine tabular alumina T60/64 -45 MY LI (BET: 0.6 m2/g, d50: 16.00 µm), were used as matrix components [7,8].
As shown in Table 1, changes in the matrix proportions resulted in refractory castables with varying specific surface areas of the Al2O3-based matrix. The aggregate fraction remained constant. In this study, the designation of the model castables refers to the specific surface area of the ceramic matrix (Al2O3 raw materials). For example, a castable with a specific surface area of the matrix of 1.0 m2/g is designated as ‘Castable 1.0 m2/g’, thereby directly reflecting the matrix’s specific surface area in the sample name [7,8].
Three dispersing agent systems with different dispersion mechanisms (steric and electrosteric) were selected at graded concentrations (Table 2): a polycarboxylate ether (PCE, Castament FS60 (BASF Construction Polymers GmbH, Trostberg, Germany)); a polymethacrylate (PMA, Darvan 7S (Vanderbilt Minerals, LLC, Norwalk, CT, USA)) combined with citric acid (food grade); and a sodium tripolyphosphate (S-TPP, N25-15 (Chemische Fabrik Budenheim KG, Budenheim, Germany)) combined with citric acid. The concentrations of each dispersing agent and the water content of the castables were experimentally determined in preliminary tests [7,8].
The exact castable compositions and preparation procedures are described in detail in Holleyn et al. [7,8].
2.1.2. Matrix Suspension Compositions and Their Preparation
Representative matrix suspensions were investigated to gain insights into the rheological behaviour of the model refractory castables. Compositions with a specific surface area of the matrix of 1.0, 2.7, and 4.7 m2/g were analysed. The PCE dispersing agent Castament FS60 was employed at two different concentrations, corresponding to concentrations of 0.075 and 0.15 wt.% in the fully composed castables (Table 2). The suspension formulations were derived by removing all Al2O3 fractions larger than 45 µm from the respective refractory castables (Table 1). The exact matrix suspension compositions and preparation procedures are described in detail in Holleyn et al. [7].
| BET in m2/g | 1.0 | 1.3 | 2.7 | 3.0 | 4.5 | 4.7 |
| d50 in µm | 7.1 | 3.2 | 3.0 | 1.8 | 1.4 | 2.0 |
| Component in wt.% | ||||||
| Al2O3 | ||||||
| T60/64 0–6 mm | 69 | 69 | 69 | 69 | 69 | 69 |
| T60/64 -45 MY LI | 16 | 9 | 9 | - | - | 9 |
| Reactive alumina (CTC20) | 10 | 17 | 10 | 19 | 12 | - |
| Reactive alumina (RG4000) | - | - | 7 | 7 | 14 | 17 |
| CA-cement (70 wt.% Al2O3) | 5 | 5 | 5 | 5 | 5 | 5 |
| Sum | 100 | 100 | 100 | 100 | 100 | 100 |
| Water | depending on the dispersing agent (Table 2) | |||||
| Dispersing agent | Table 2 | |||||
Table 2. Dispersing agents, concentrations, and water amount [7,8].
|
Dispersing Agent System |
Dispersing Agent |
Amount in wt.% |
Water in wt.% |
|---|---|---|---|
|
Polycarboxylate ether (PCE) |
Castament FS60 |
0.075/0.10/0.15 |
4.8 |
|
Polymethacrylate (PMA) |
Darvan 7S + Citric acid |
0.07/0.10/0.13 0.01 |
6.3 |
|
Sodium tripolyphosphate (S-TPP) |
N25-15 + Citric acid |
0.05 0.010/0.015/0.020 |
6.7 |
2.2. Experimental Methods
Measurements of the dynamic viscosity (absolute values) of the matrix suspensions were conducted using a rheometer (Haake Mars 40, Thermo Fisher Scientific, Waltham, MA, USA) equipped with a coaxial cylinder measurement geometry (CCB25 DIN/Ti). The measurement program followed a step-wise shear program, covering a shear rate range from 10 to 1000 s−1 in 25 increments. Each shear step was maintained for 20 s, and measurements were recorded after stabilization was achieved. The tests were performed at a temperature of 20 °C. Extended measurement and stabilization times were avoided to prevent initial stiffening of the suspension, which could distort the results. For a comprehensive interpretation, however, the opposite effect should also be considered, namely that suspensions may further disperse during the measurement. The same procedure was applied as described in preliminary investigations by Holleyn et al. [7].
The rheological behaviour of the refractory castables was determined directly using a building material rheometer (Viskomat NT, Schleibinger Geräte Teubert u. Greim GmbH, Buchbach, Germany) immediately after mixing, with the results expressed as relative values. A spherical measuring geometry was used. The sphere was fully immersed in the refractory castable and rotated through three-quarters of a turn, ensuring it did not return to an area that had already been sheared. The measurement profile selected was a ramp profile with different shear rates (rotational speeds), in order to map flow curves using a shear test. After immersing the measuring sphere into the castable material and waiting 1 min to allow the castable material to flow back together as homogeneously as possible around the sphere, the sphere was rotated at increasing speeds up to 5.0 rpm (1 s to 0.001 rpm, 5 s to 0.01 rpm, 6 s to 5.0 rpm and then held at 5.0 rpm for 4 s). The sphere’s speed was then decreased at the same rate. This deceleration phase was analysed for the measurements. By gradually lowering the speed, different shear rates (rotational speeds) could be represented. During the measurement, material accumulates in front of the sphere mount. If an accelerated movement measurement profile were applied, material would accumulate to a greater extent in front of the measuring sphere mount, increasing the measurement error. With a decelerated movement, material also accumulates; however, since the total mass remains constant, the resulting error does not increase, thereby improving measurement accuracy.
The Viskomat NT measures speed and torque, which can be related to the rheological variables of shear rate and shear stress. Mean values were formed from the measured values in equilibrium, and a Herschel-Bulkley regression was performed according to Equation (2) to mathematically describe the flow curve [5,15,16,17,18,19,20,21]. The regression of the measurement data was carried out using Microsoft Excel® and the associated add-in tool ‘Solver’. Accordingly, values for the relative yield stress and relative viscosity, as well as for n, which characterises the curvature of the flow curve, can be determined for each of the refractory castables analysed under the described measurement conditions. The coefficient of determination R2 was also calculated in each case to analyse how well the model fits the actual measured values. The measuring system used does not allow the determination of absolute rheological parameters, as the spherical measurement geometry does not define a distinct sheared surface and the experiment is performed within a three-dimensional interference field. This means that the shear gradient cannot be determined precisely. Therefore, the result of the measurement is a relative measure of the rheological behaviour of the model castables. However, comparative analyses are possible if the measurements are carried out under identical or at least comparable conditions [19,22]. Although there have been attempts to determine absolute values for the shear rate dependant dynamic viscosity of fully composed castables, these have not yet been completely developed or verified [30]. The mass temperatures of the model castables directly after mixing were measured.
Immediately after mixing, the rheological behaviour of the model castables was investigated indirectly through 3D slump-flow measurements (using a measuring cylinder geometry according to DIN EN ISO 1927-4 for self-flowing castables) to evaluate their processing characteristics. Image acquisition was carried out using a high-resolution processing platform with an integrated area camera (model CV-X/XG-X, Keyence, Neu-Isenburg, Germany). A 3D point cloud was generated via fringe projection, combining data from a high-speed camera and structured light provided by eight projectors. This setup minimises shadowing effects and reflection artifacts. The image data were processed by the manufacturer’s own integrated image processing software, which calculates parameters such as diameter, height, 3D topography, and the percentage area growth based on a binary representation of the image data. This approach provided a comprehensive documentation of the castables’ flow behaviour. The respective temperatures of the refractory castables immediately after the mixing process were taken into account in the evaluation.
At the time of measurement using the building rheometer or the 3D slump-flow test, neither the initial stiffening of the castables nor hydration is to be expected. This has been confirmed by conducting sonic velocity measurements on all the refractory castables under consideration [8].
3. Results and Discussion
3.1. Dynamic Viscosity of the Matrix Suspensions
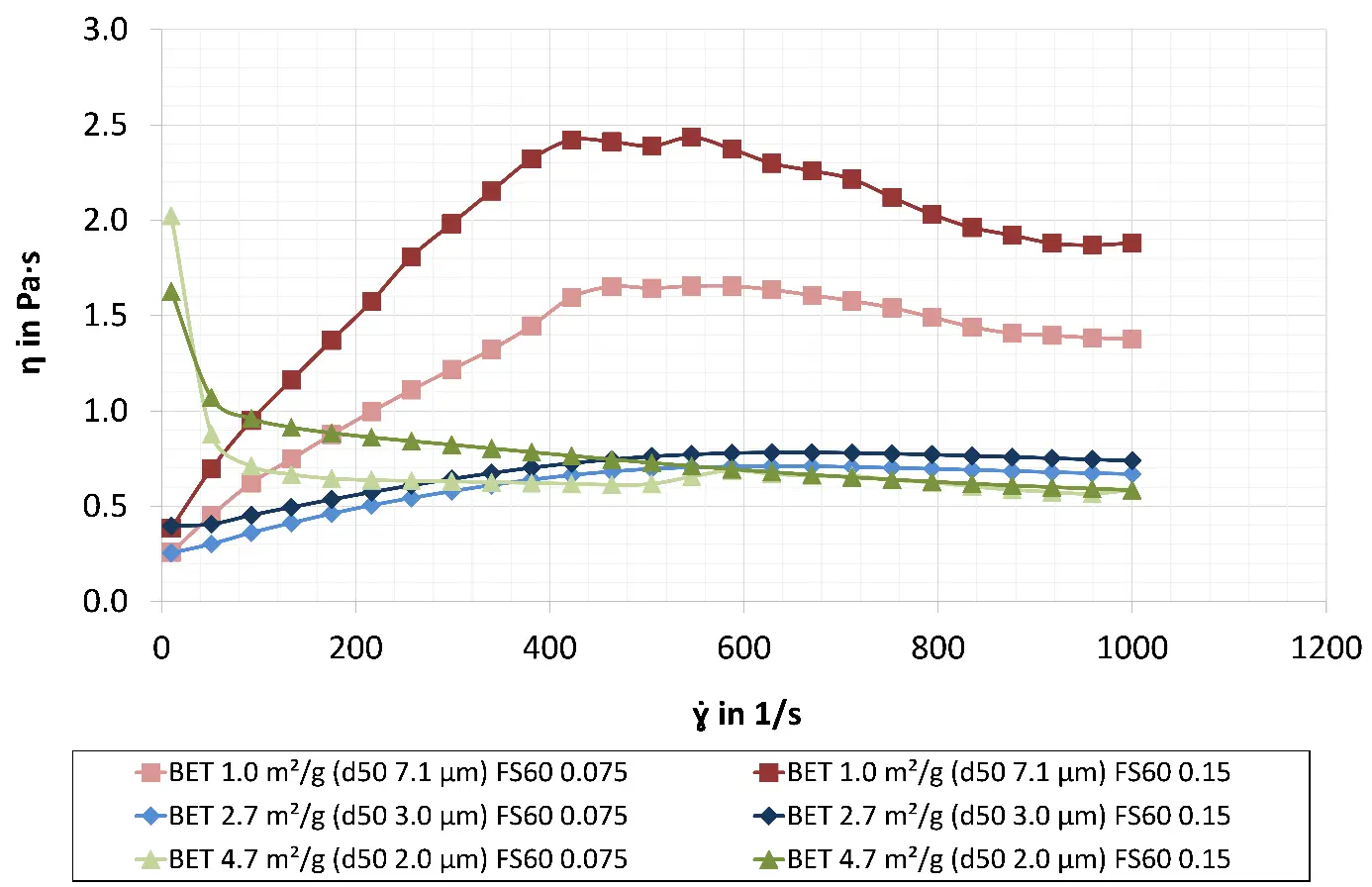
In Figure 2, the dynamic viscosity measurements of matrix suspensions dispersed with PCE (Castament FS60) are depicted as a function of the shear rate:
-
-
The matrix suspensions with a specific surface area of 1.0 m2/g showed dynamic viscosities of up to 1.66 (0.075 wt.% FS60) and 2.44 Pa·s (0.15 wt.% FS60) at elevated shear rates. These are the highest recorded values in this series of experiments at high shear rates. However, the dynamic viscosity increases with increasing shear rate up to a point, followed by a slight decrease. This behaviour may be attributed to particle settling during the measurement, which reduces the particle concentration near the main measuring surface and consequently decreases the viscosity at high shear rates. Structural rupture may contribute to the decrease in viscosity at high shear rates. Wall slip can occur and should therefore be considered. At very low shear rates, low values of 0.26 (0.075 wt.% FS60) and 0.38 Pa·s (0.15 wt.% FS60) are attained. As the shear rate increases, the suspensions exhibit shear thickening behaviour. Büchel et al. [24] reported that improper control of the matrix composition can lead to increased flow resistance and shear thickening behaviour when pumping refractory castables (which corresponds to high shear rates). These findings suggest that interlocking of coarse particles within the matrix during material movement, arising from a coarse particle composition (with a low specific surface area), is responsible for the observed shear thickening behaviour.
-
-
The suspensions with a higher specific surface area of 2.7 m2/g exhibit comparable dynamic viscosity values of 0.25 and 0.40 Pa·s (0.075 and 0.15 wt.% FS60, respectively) at low shear rates and considerably lower values (compared to matrix suspensions with a specific surface area of 1.0 m2/g) of 0.71 and 0.78 Pa·s (0.075 and 0.15 wt.% FS60, respectively) at higher shear rates. As the shear rate increases, the flow curve remains nearly constant. This apparent plateau may result from the simultaneous occurrence of shear thinning and shear thickening behaviour within the considered shear rate range, and could be described as pseudo-Newtonian behaviour. This rheological behaviour can be attributed to the multimodal composition (and the broadest particle size distribution) of the matrix suspensions/castables with a specific surface area of 2.7 m2/g (Table 1). The use of multimodal particle distributions in the matrix of refractory castables has already been described in the literature in terms of reducing viscosity and improving flow behaviour [6,9,23,24,25].
-
-
The matrix suspension with the highest specific surface area of 4.7 m2/g exhibits shear thinning behaviour at low shear rates. The initial dynamic viscosity values were 1.63 and 2.02 Pa·s (0.15 and 0.075 wt.% FS60, respectively). The values are markedly higher than those of the other suspensions analysed, which is likely due to the higher proportion of the finest component (reactive alumina RG4000 with a specific surface area of 6.9 m2/g). At elevated shear rates, the dynamic viscosity for both dispersing agent concentrations declines to 0.59 Pa·s, representing the lowest values observed in this series of experiments at high shear rates. The high specific surface area of the particles can account for this rheological behaviour. In the resting state, numerous interparticle forces are built up, resulting in high viscosity. As the shear rate increases, these adhesive forces are progressively overcome, leading to a decrease in dynamic viscosity [9].
A general trend of higher dispersing agent concentrations leading to lower viscosity values cannot be observed, rather, the opposite appears to be the case. This may be explained by the entanglement of long-chain molecules of the dispersing agents (at higher concentrations), which could lead to increased viscosity. The matrix suspensions of the other dispersing agent systems exhibited similar rheological behaviour, although it was less pronounced due to the higher water content required, which results from the lower dispersion efficiency of PMA and S-TPP compared to PCE. The results of the dynamic viscosity measurements of these matrix suspensions are described in detail by Holleyn et al. [7].
3.2. Temperature of the Castables after Mixing Process
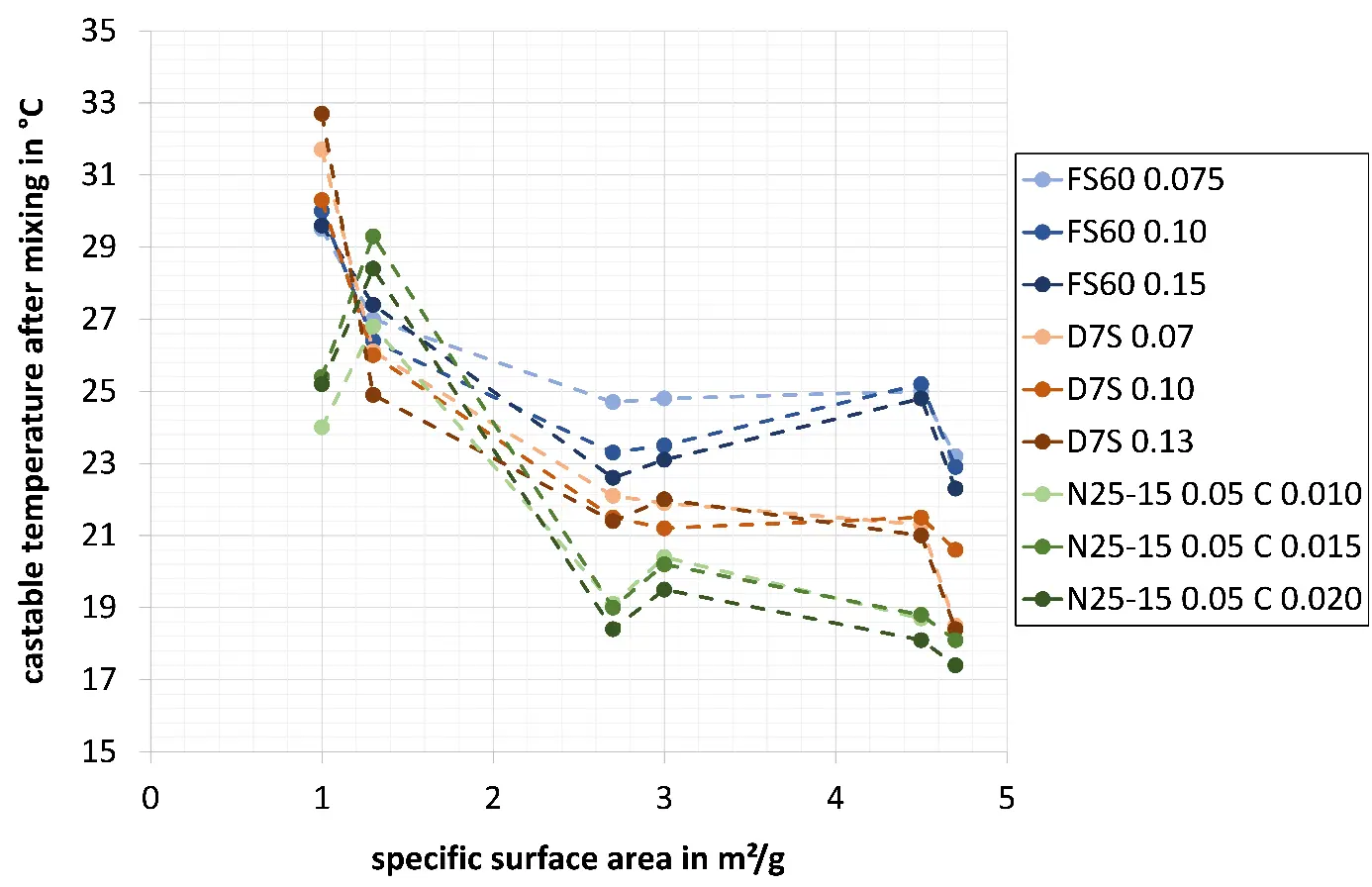
The refractory castable properties, such as rheological and flow behaviour are influenced by temperature. An increase in castable temperature can lead to a reduction in yield stress and viscosity [18,19,31,36]. One possible explanation for this is that thermally excited movements reduce interparticle friction and stabilising forces of the suspension’s structure [19]. There are clear differences in the castable temperature after mixing, which are primarily due to the varying specific surface areas of the matrix (and also the dispersing agent used, which affects the required water content). The warming of the castables is mainly caused by the mixing process (and also by the room, raw materials and water temperature). Figure 3 shows the measured temperatures directly after the refractory castables were mixed.
The following trends can be recognised:
-
-
With increasing specific surface area of the matrix, the refractory castables heat up less during mixing. Castables with higher specific surface areas tend to exhibit Bingham (with low yield stress) or shear thinning behaviour, requiring less mixing energy than castables with lower specific surface areas, which display shear thickening behaviour. As a result, castables with higher specific surface areas heat up less [7]. Castables with a high specific surface area (4.7 m2/g) reached temperatures between 17.4 and 23.2 °C, whereas those with a low specific surface area (1.0 m2/g) reached higher values between 24.0 and 32.7 °C.
-
-
The influence of the dispersing agent system used is indirectly reflected in the temperature of the castables. Model castables dispersed with PCE (Castament FS60) exhibit higher temperatures after mixing than those dispersed with PMA (Darvan 7S in combination with citric acid). The lowest temperatures are observed for castables dispersed with S-TPP (N25-15) and citric acid. The main influencing parameter is the differing water demand, which increases in the following order: 4.8 wt.%, 6.3 wt.%, and 6.7 wt.% (Table 1 and Table 2). Adjustments of the water content were necessary due to the reduced dispersion strength of PMA and S-TPP compared to PCE. A higher water content reduces interparticle forces at the high shear rates generated during mixing, resulting in castables with a higher water content heating up less [7].
-
-
In most cases, higher concentrations of the respective dispersing agents result in lower castable temperatures after mixing. This effect can be attributed to the lower mixing energy required when more dispersing agent is used [7]. The concentration of the dispersing agents therefore, plays a significant role, particularly at the high shear rates occurring during mixing. Increasing the dispersing agent concentration enhances dispersion efficiency, thereby reducing interparticle forces and consequently lowering the temperature rise of the castable.
-
-
Model refractory castables with a more monomodal distribution of the matrix (as in the case of 3.0 m2/g) due to a high proportion of a single particle fraction ((19 wt.% of CTC20), Table 1) tend to exhibit shear thickening behaviour (although weakly pronounced) [5,9]. This behaviour requires higher mixing energy, resulting in (slightly) elevated mass temperatures [7]. In contrast, multimodal compositions of the matrix (2.7 m2/g, Table 1) can reduce the required mixing energy [6,9,23,24,25], leading to lower castable temperatures. These effects, however, necessitate further experimental verification.
3.3. Rheological Behaviour of the Castables
The rheological behaviour of the model refractory castables with varying specific surface areas, dispersed with the PCE dispersing agent Castament FS60 at a concentration of 0.15 wt.% (Table 1 and Table 2), is shown in Figure 4. The figure also presents the corresponding equations describing the respective flow curve progressions. Regression curves of the mean values of experimental measuring points were calculated using the Herschel-Bulkley model (Equation (2)) [5,15,16,17,18,19,20,21]. With values ranging from 0.946 to 0.999, the coefficient of determination R2 is considered to be in a very good range. Different curve progressions can be clearly recognised. A systematic correlation can be observed between the rheological behaviour and the specific surface area of the refractory castable matrix; however, this applies only in relative terms, not as absolute values:
-
-
The castables with specific surface areas of the matrix of 1.0 and 1.3 m2/g clearly display shear thickening behaviour when shear is increased, as can be seen from the progressive curve. The values for n demonstrate this, with n > 1 at 1.4 and 1.3, respectively. At a low shear rate, the castables show low values of shear stress. With increased shear, these values increase disproportionately. Shear thickening behaviour with an increasing shear rate was also observed in the corresponding matrix suspension (1.0 m2/g, Figure 2). As previously explained, the interlocking of larger particles as a consequence of the coarse matrix composition (with a low specific surface area) leads to shear thickening behaviour during material movement [24]. The relative yield stress of castable 1.0 m2/g is very low at 0.5 N·mm, and that of 1.3 m2/g is 1.6 N·mm. These are the lowest values in this series of measurements, indicating that a minimal force is required to achieve flow of the castables at very low shear rates. A correlation with the matrix suspension with the specific surface area of 1.0 m2/g can be established, as very low dynamic viscosities are measured in the low shear rate range (Figure 2). The increased mass temperatures of the castables with low specific surface areas of the matrix (Figure 3, see explanation of the temperature differences in Section 3.2) can also contribute to a low yield stress [18,19,31,36]. The relative viscosity of these formulations is 15.2 N·mm·minn (1.0 m2/g) and 6.1 N·mm·minn (1.3 m2/g).
-
-
Castables with a higher specific surface area of the matrix of 2.7 and 3.0 m2/g (2.7 m2/g also has the broadest particle size distribution) show Bingham behaviour (with low yield stress), which is confirmed by n = 1. The relative shear stress increases proportionally over the entire relative shear rate range. The multimodal composition of the castable matrix (Table 1) positively influences its flow behaviour [6,9,23,24,25]. Due to the intermediate specific surface area and the broad particle size distribution, it is possible that shear thinning and shear thickening behaviour overlap simultaneously. Within the shear rate range under consideration, this results in Bingham behaviour (with low yield stress). Matrix suspensions 2.7 m2/g also show pseudo-Newtonian flow over the entire shear rate range (for the reasons just mentioned (Figure 2)). The relative yield stress of the castables is quite similar, at 4.6 N·mm (2.7 m2/g) and 3.4 N·mm (3.0 m2/g). The relative viscosities of both refractory castables are comparable, at 7.7 N·mm·minn (2.7 m2/g) and 6.2 N·mm·minn (3.0 m2/g), respectively. These relative viscosity values are in the lower range of this series of measurements.
-
-
Castables with a specific surface area of the matrix of 4.5 and 4.7 m2/g exhibit shear thinning behaviour , as indicated by the degressive progression of the flow curve. This is clearly described by the values of n < 1, at 0.8 and 0.6, respectively. At low shear rates, the castables exhibit high values for shear stress. As the shear rate increases, however, the curve flattens out and the shear stress values become disproportionately low. For castable 4.5 m2/g, a high value for the relative yield stress of 20.2 N·mm and a high relative viscosity of 10.7 N·mm·minn are determined. The castable with a specific surface area of 4.7 m2/g provides a very high relative yield stress of 40.9 N·mm and a very high relative viscosity of 47.7 N·mm·minn. As shown in Figure 2, the corresponding matrix suspensions (4.7 m2/g) also display shear thinning behaviour when the shear rate increases. At very low shear rates, the suspensions exhibit high dynamic viscosities, which decrease significantly at higher shear rates. This can be attributed to the increased proportion of the finest component (reactive alumina RG4000 with a specific surface area of 6.9 m2/g) in both the real castables and the matrix suspensions. One explanation for this is the particle’s high specific surface area. In the resting state, interparticle forces build up, leading to high viscosity. Increasing shear reduces these forces and decreases viscosity [9].
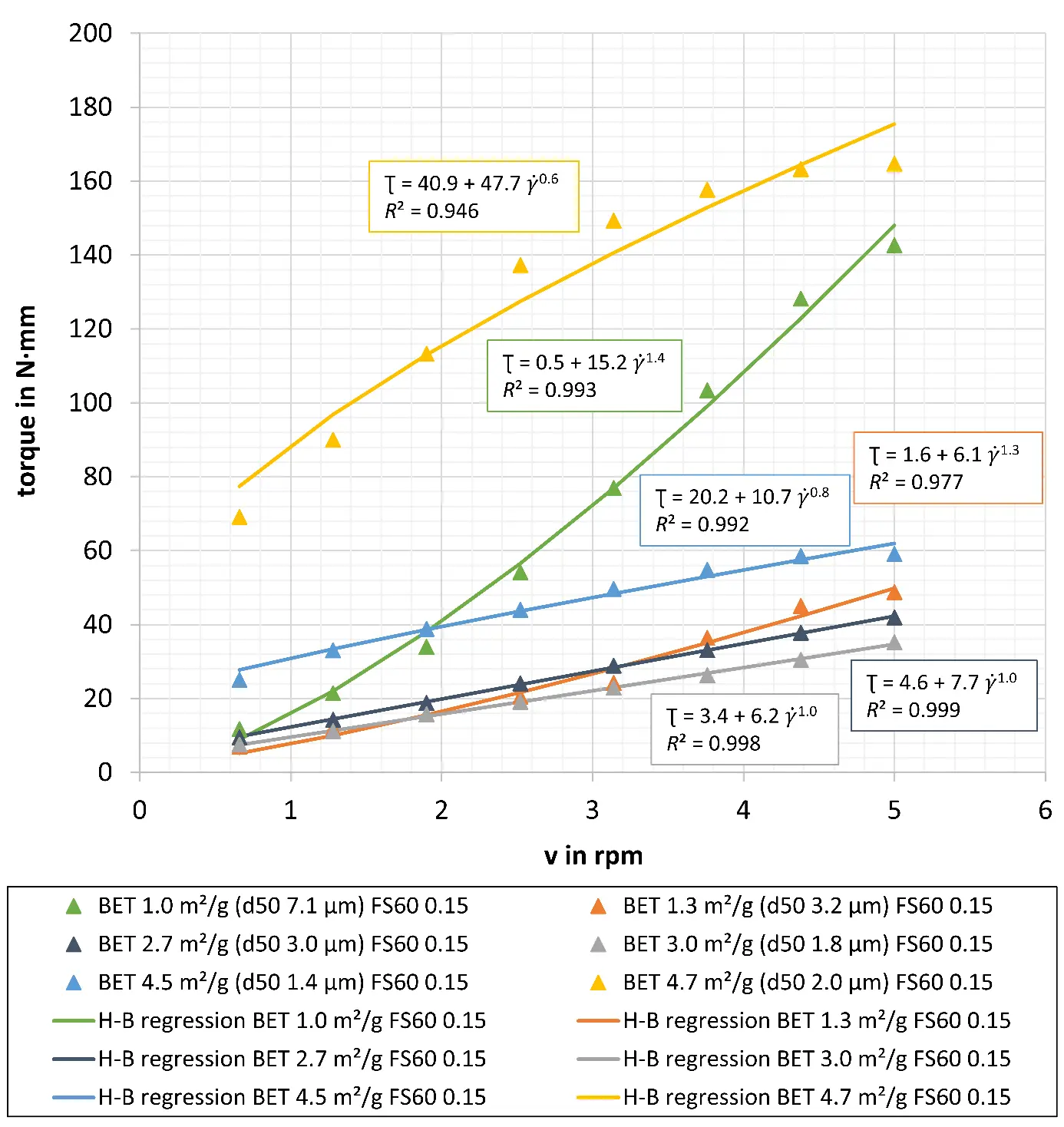
Figure 4. Rheological behaviour (regression curve according to Herschel-Bulkley model (Equation (2)): relative yield stress (Ʈ0) in N·mm, relative viscosity (k) in N·mm·minn, value for n, coefficient of determination R2) of the refractory castables with different specific surface areas of the matrix and the PCE dispersing agent Castament FS60 in a concentration of 0.15 wt.% (Table 1 and Table 2).
The trends and correlations observed in this series of measurements (with the same explanations) can also be observed in other rheological measurements of the model refractory castables containing different dispersing agents at graded concentrations (Table 1 and Table 2). To provide a comprehensive comparison, Figure 5, Figure 6 and Figure 7 plot the parameters from the Herschel-Bulkley regression equations (n, Ʈ0, and k from Equation (2)), which describe the flow curve progressions and, therefore the rheological behaviour of the refractory castables, against the specific surface area of the matrix.
The values of n, relative yield stress (Ʈ0), and relative viscosity (k) could not be determined for the following castables with a low specific surface area of 1.0 m2/g: 0.075 wt.% Castament FS60; 0.07 and 0.10 wt.% Darvan 7S (in combination with citric acid); and 0.05 wt.% N25-15 with 0.010, 0.015, and 0.020 wt.% citric acid. Similarly, no values could be obtained for the castable with a specific surface area of 1.3 m2/g containing 0.05 wt.% N25-15 and 0.010 wt.% citric acid. These castables most likely exhibited yield stresses so high that no measurement data could be recorded, as the rheometer stopped upon reaching its predefined overload limit. This indirectly reflects the comparatively lower dispersion efficiency of PMA and S-TPP relative to PCE, as well as the dependence on the dispersing agent concentration in castables with very low specific surface areas.
No values for the parameters could be determined for the castable with a specific surface area of 4.7 m2/g with 0.05 wt.% N25-15 and 0.010 wt.% citric acid. The refractory castable stiffened very quickly after mixing. This can be attributed to the high specific surface area, which leads to extensive adsorption of citric acid, leaving only a small amount dissolved in the pore water. When Ca2+ is released from CA-cement during dissolution, free citric acid is rapidly consumed, and adsorbed citric acid is desorbed from the particle surfaces, inducing coagulation of the matrix suspension.
As shown in Figure 5, the model castables with low specific surface areas of the matrix (1.0 and 1.3 m2/g) exhibit shear thickening behaviour (n > 1) with n ranging from 1.0 to 1.8 [24]. The higher specific surface area of the castables 2.7 and 3.0 m2/g (2.7 m2/g also has the broadest particle size distribution due to its multimodal composition) leads to values of n ≈ 1 (0.9; 1.0; 1.1), which describe Bingham behaviour (with low yield stress) (probably due to the overlap of shear thickening and shear thinning behaviour) over the considered shear rate range [6,9,23,24,25]. For castables with a specific surface area of 4.5 and 4.7 m2/g, values of n < 1 ranging from 0.6 to 1.0 describe shear thinning behaviour. This can be explained by the presence of high interparticle forces at low shear rates [9], which decrease with increased shear, thereby improving flow due to a reduction in relative viscosity.
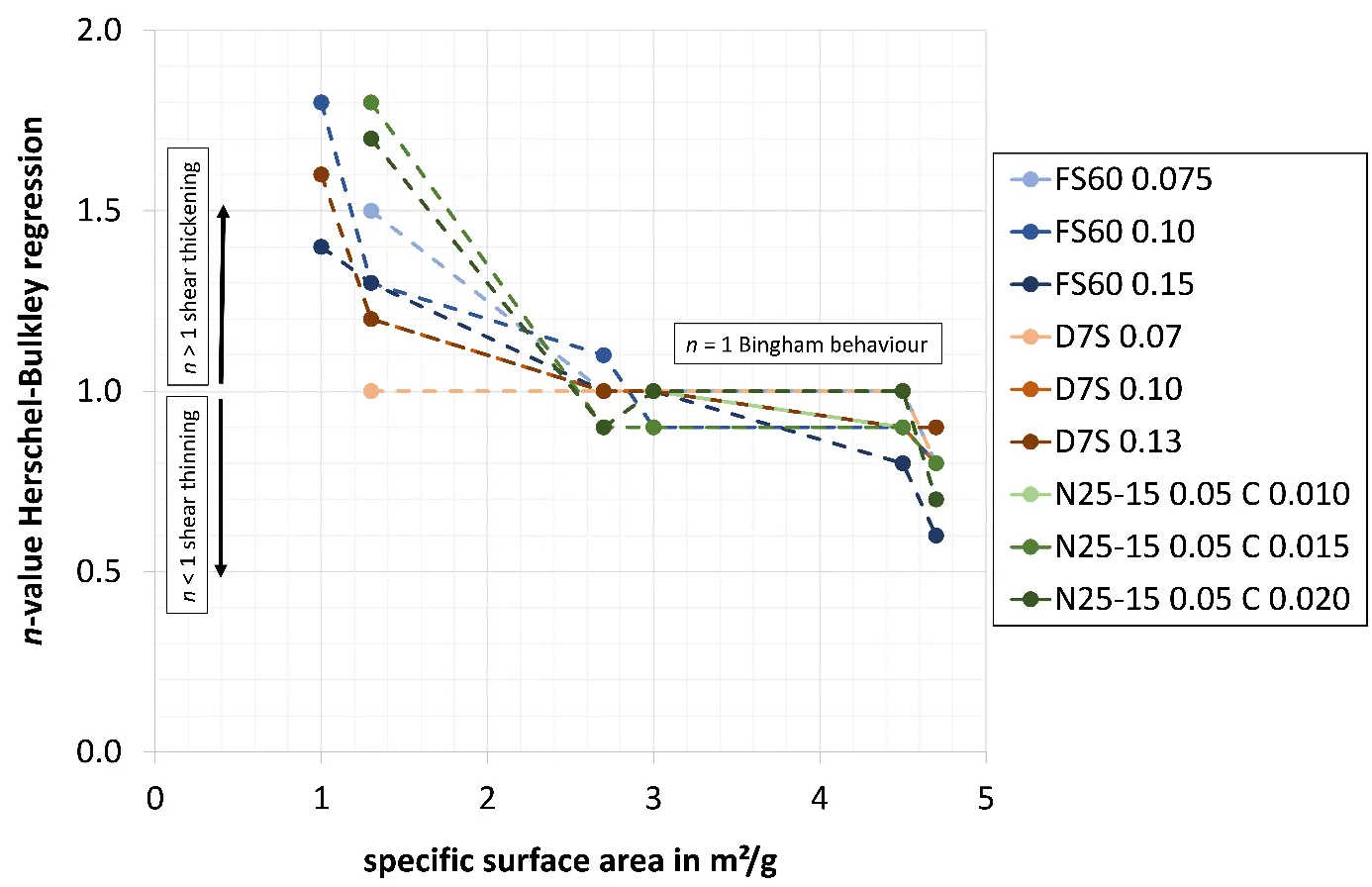
Figure 5. Value for n (parameter from the regression according to Herschel-Bulkley model (Equation (2)) of all refractory castables with different specific surface areas of the matrix, dispersing agents and concentrations (Table 1 and Table 2).
For all refractory castables with different dispersing agents and concentrations, a clear trend of increasing relative yield stress is observed with higher specific surface area (Figure 6). Initially, the relative viscosity decreases as the specific surface area of the matrix increases, before rising sharply again (Figure 7):
-
-
Castables with a low specific surface area of the matrix (1.0 and 1.3 m2/g) display shear thickening behaviour [24], showing a value of zero (no yield stress) or very low values for the relative yield stress (0.0 to 9.0 N·mm) and relative viscosities of 4.6 to 31.0 N·mm·minn. Matrix suspensions with a specific surface area of 1.0 m2/g, as shown in Figure 2, exhibit very low dynamic viscosities at low shear rates. There is a clear correlation with the non-existent (value of zero) or very low relative yield stress of the castables. The higher castable temperature (Figure 3, see explanation for the differences in castable temperatures in Section 3.2) can also contribute to low yield stress. For castables with a specific surface area of 1.3 m2/g, lower relative viscosities of 4.6 to 10.2 N·mm·minn were determined when using PCE (Castament FS60), despite the lower required water content due to the higher dispersion strength, compared to PMA (Darvan 7S in combination with citric acid), which produced relative viscosities of 8.5 to 10.5 N·mm·minn, and S-TPP (N25-15) with citric acid, which resulted in relative viscosities of 7.3 to 13.7 N·mm·minn. Interpreted cautiously, the performance of this PCE appears to be superior at very low specific surface areas compared to PMA and S-TPP.
-
-
The higher specific surface area of castables 2.7 and 3.0 m2/g (2.7 m2/g also has the broadest particle size distribution due to its multimodal composition (Table 1)) results in low to medium relative yield stress of 0.6 to 15.4 N·mm and to low values for the relative viscosity [6,9,23,24,25] of 2.0 to 13.2 N·mm·minn. For all refractory castables 3.0 m2/g, the relative yield stress and also the relative viscosity are somewhat lower than for the refractory castables with a specific surface area of 2.7 m2/g. As can be seen from Figure 3, castables with a specific surface area of 3.0 m2/g heat up slightly more during the mixing process, leading to higher mass temperatures (see explanation for the differences in castable temperatures under Section 3.2). These increased temperatures are likely to be the reason for the reduced values of relative yield stress and relative viscosity [18,19,31,36].
-
-
Due to their high specific surface area, castables 4.5 and especially 4.7 m2/g exhibit shear thinning behaviour, which is attributed to strong interparticle forces [9]. This leads to high relative yield stress of 2.1 to 49.0 N·mm and high values for the relative viscosity of 3.0 to 47.7 N·mm·minn. There is a clear correlation with the rheological behaviour of the matrix suspensions 4.7 m2/g that display high values for the dynamic viscosity at very low shear rates (Figure 2). The gradation of lower values for S-TPP and citric acid, higher values for PMA (in combination with citric acid), and very high values for PCE is clearly visible in the relative yield stress and relative viscosity of castables 4.7 m2/g. This can be explained by the higher required water contents of 6.7 wt.% (S-TPP), 6.3 wt.% (PMA) and 4.8 wt.% (PCE), which result from the differing dispersion strengths of the dispersing agents.

Figure 6. Relative yield stress (Ʈ0, parameter from the regression according to Herschel-Bulkley model (Equation (2)) of all refractory castables with different specific surface areas of the matrix, dispersing agents, and concentrations (Table 1 and Table 2).
The influence of the dispersing agent concentration on rheological parameters is difficult to interpret. For PCE (Castament FS60), almost no dependence on concentration is observed. For PMA (Darvan 7S in combination with citric acid), the effect of concentration on rheology appears indifferent. In case of S-TPP (N25-15 with citric acid), a higher citric acid content leads to a lower relative yield stress and a lower relative viscosity. Nevertheless, it is evident that all dispersing agent systems investigated (particularly PCE, owing to its high dispersion strength) perform well even at very low concentrations. Independent of the system used, temperature differences can act as disturbance variables, since castable temperatures (induced by the mixing process) may influence both yield stress and viscosity [18,19,31,36].
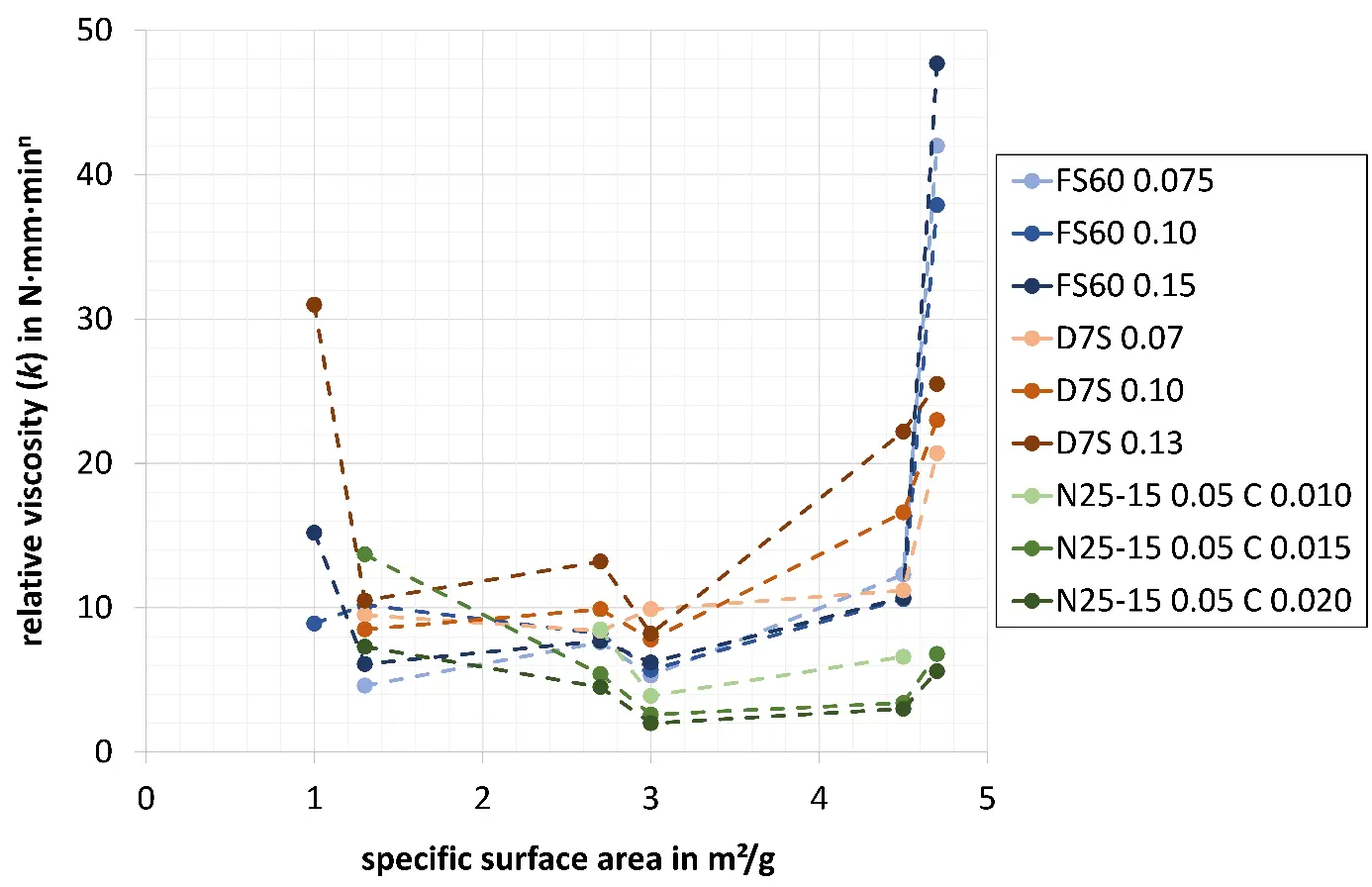
Figure 7. Relative viscosity (k, parameter from the regression according to Herschel-Bulkley model (Equation (2)) of all refractory castables with different specific surface areas of the matrix, dispersing agents and concentrations (Table 1 and Table 2).
3.4. 3D Slump-Flow of the Castables
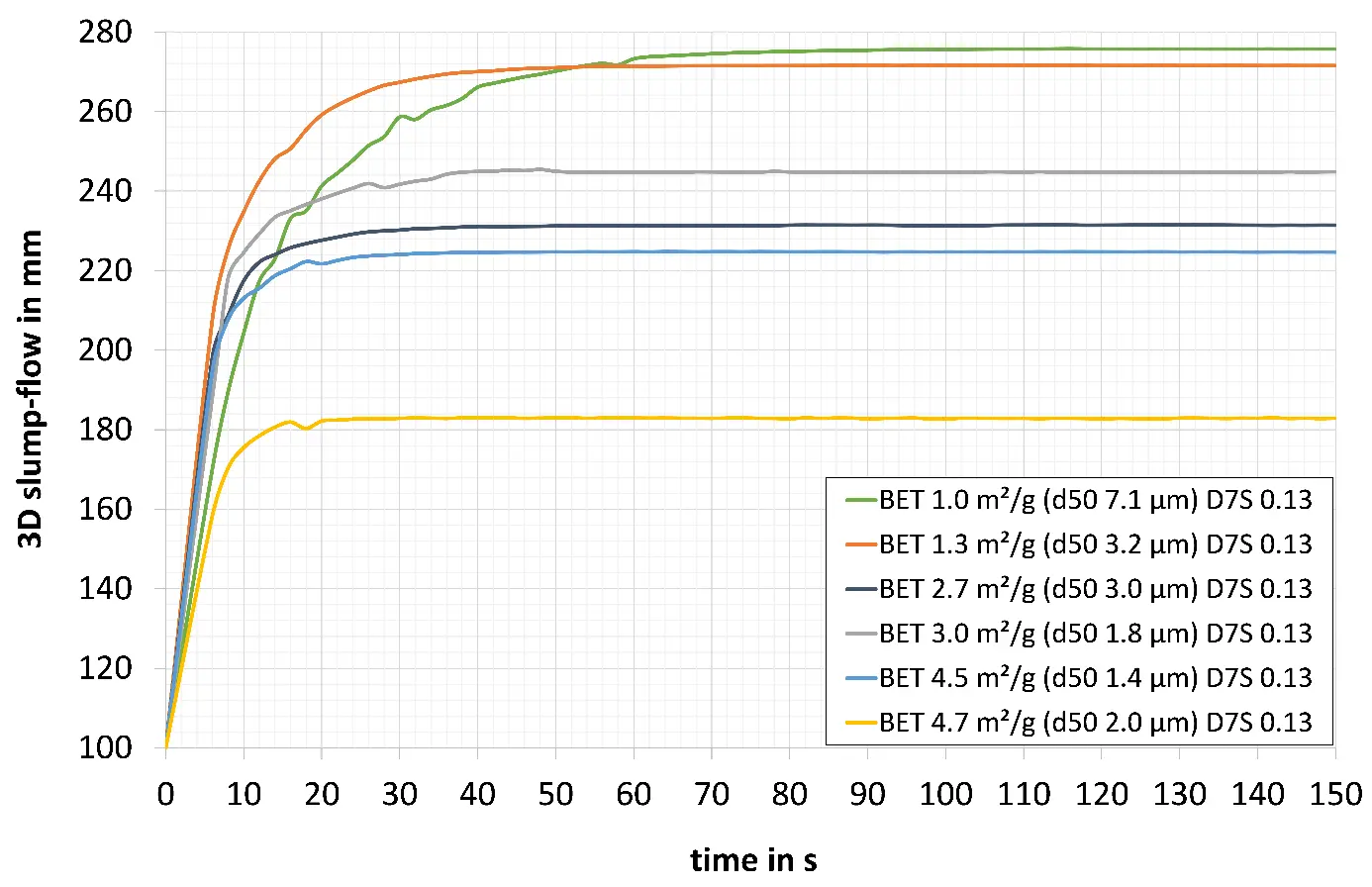
Figure 8 shows the 3D slump-flow of the model refractory castables with different specific surface areas and the PMA dispersing agent Darvan 7S (in combination with citric acid) at a concentration of 0.13 wt.% (Table 1 and Table 2). Clear differences in flow behaviour are evident depending on the specific surface area of the castable’s matrix. The slope of the curve in the first few seconds of the measurement provides an indication of the flow rate (no measured values, but interpolation). The final values of the curves show the maximum 3D slump-flow:
-
-
Castable 1.0 m2/g shows the highest maximum 3D slump-flow with 276 mm. The maximum 3D slump-flow of castable 1.3 m2/g is 272 mm. The spreading of self-flowing refractory castables is subject to (very) low shear rates. The very low relative yield stress of these model castables (0.0 N·mm at 1.0 m2/g and 2.9 N·mm at 1.3 m2/g (Figure 6)) is probably further promoted by high castable temperatures (Figure 3, see explanation for the differences in castable temperatures under Section 3.2). The low dynamic viscosity of the matrix suspensions 1.0 m2/g in the low shear rate range also correlates with a high slump-flow of the castable [7]. The high slope of the straight line during the initial seconds of the flow of castable 1.3 m2/g indicates a high flow velocity. The low specific surface area of 1.0 and 1.3 m2/g results in relatively low interparticle forces, favouring a broad and rapid flow.
-
-
Refractory castable 2.7 m2/g provides a maximum 3D slump-flow of 231 mm. The castable 3.0 m2/g achieves a slightly higher maximum 3D slump-flow value of 245 mm. With 7.7 and 8.1 N·mm, the values for the relative yield stress of these castables (Figure 6) are higher than those of 1.0 and 1.3 m2/g, which explains why the maximum 3D slump-flow is smaller. The higher value for the castable with a specific surface area of the matrix of 3.0 m2/g compared to 2.7 m2/g can be explained by the lower relative viscosity of 8.2 N·mm·minn (3.0 m2/g) compared to 13.2 N·mm·minn (2.7 m2/g) (Figure 7). The higher temperature of the model castable 3.0 m2/g of 22.0 °C to 21.4 °C at 2.7 m2/g (Figure 3, see explanation for the differences in castable temperatures under Section 3.2) could lead to lower values for the relative viscosity [18,19,31,36], resulting in a larger maximum 3D slump-flow.
-
-
The refractory castables with the highest specific surface areas of 4.5 and 4.7 m2/g show the lowest values for the maximum 3D slump-flow (225 and 183 mm, respectively) within this series of measurements. Due to the high specific surface area of the matrix, and thus strong interparticle forces [9], the model castables exhibit a high relative yield stress of 14.0 N·mm (4.5 m2/g) and 18.0 N·mm (4.7 m2/g) (Figure 6), as well as a high relative viscosity of 22.2 N·mm·minn (4.5 m2/g) and 25.5 N·mm·minn (4.7 m2/g) (Figure 7). This results in a low maximum 3D slump-flow. The flow velocity of the castable 4.7 m2/g (slope of the curve in the first seconds of the measurement) is very low. This is due to the high relative yield stress, the high relative viscosity, and, most likely, due to its low castable temperature (Figure 3, see explanation for the differences in castable temperatures under Section 3.2). The dynamic viscosity of the corresponding matrix suspensions also reflects this behaviour. Suspensions 4.7 m2/g exhibit shear thinning behaviour, displaying high dynamic viscosity values at very low shear rates [7]. A clear correlation can be seen here between the high dynamic viscosity of the matrix suspensions and the low flow velocity, as well as the low maximum 3D slump-flow of the refractory castable 4.7 m2/g.
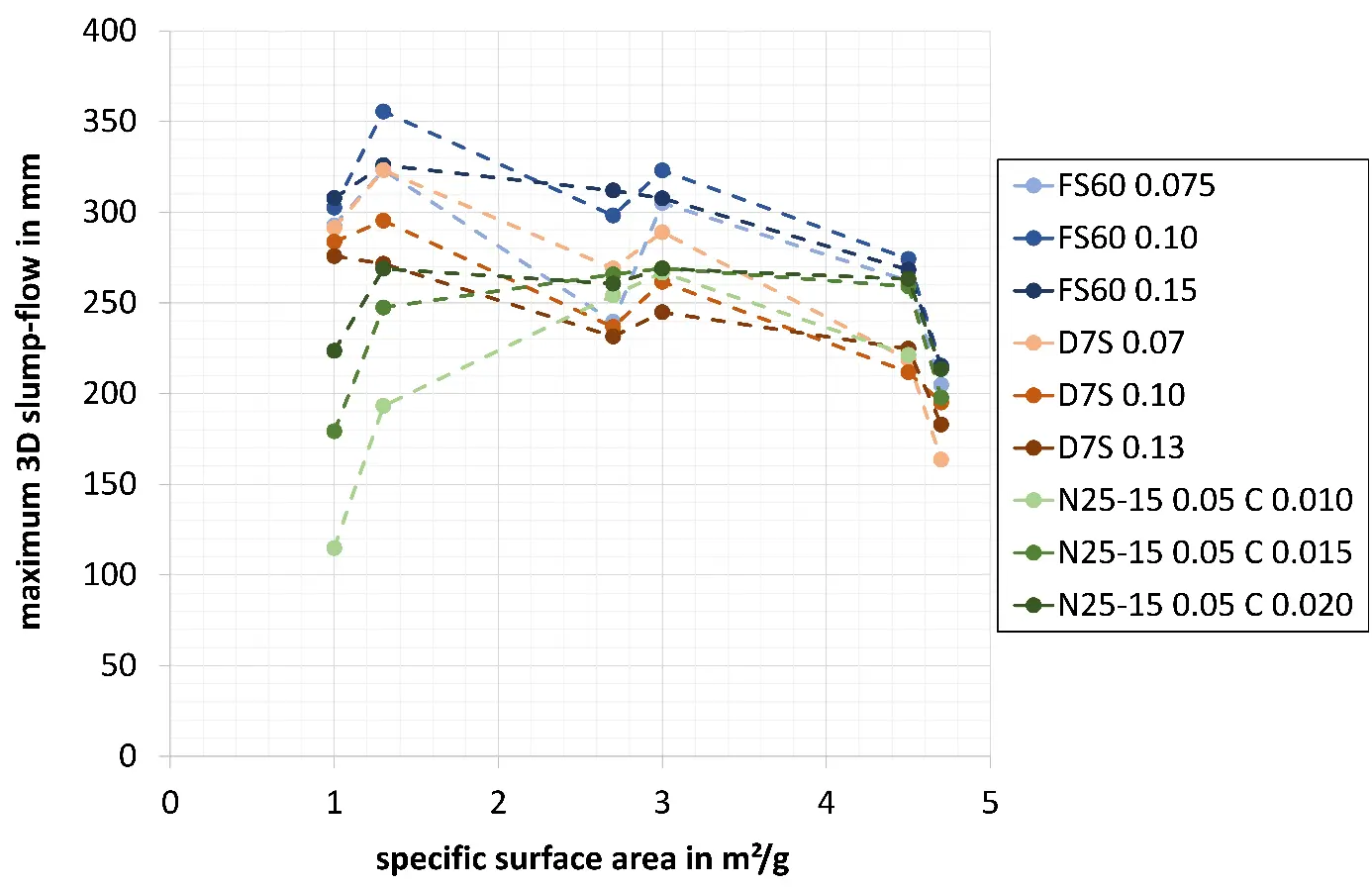
Different trends can be recognised for the maximum 3D slump-flow of model refractory castables with different dispersing agents and concentrations (Table 1 and Table 2), depending on the specific surface area of the matrix (Figure 9). The maximum 3D slump-flow values of the castables range from 114.8 to 355.5 mm.
-
-
The highest values for the maximum 3D slump-flow (when comparing the different analysed dispersing agent systems) of 204.7 to 335.5 mm were measured when using PCE (Castament FS60). Castables dispersed with PCE show a trend towards decreased maximum 3D slump-flow with higher specific surface areas. Interparticle forces increase with a higher specific surface area [9]. This leads to a much higher relative yield stress (Figure 6) and higher relative viscosity (Figure 7), resulting in lower maximum 3D slump-flow values. There is a clear correlation between the values for the slump-flow of the castables and the dynamic viscosity of the corresponding matrix suspensions at very low shear rates: Matrix suspensions dispersed with this PCE and a specific surface area of 1.0 m2/g exhibit dynamic viscosities of 0.26 and 0.38 Pa·s at very low shear rates, whereas those with a specific surface area of 4.7 m2/g show significantly higher dynamic viscosities of 1.63 and 2.02 Pa·s (Figure 2). Higher temperatures of the model castables with lower specific surface areas compared to those with higher surface areas (Figure 3, see explanation for the differences in castable temperatures in Section 3.2) may also favour this trend, as higher temperatures can cause lower relative yield stress and lower relative viscosity [18,19,31,36]. However, the increase in specific surface area is, in all probability, the dominant effect here.
-
-
Similar trends (with the same explanations) can be observed for model castables with the PMA dispersing agent Darvan 7S (in combination with citric acid). Lower maximum 3D slump-flow values, ranging from 163.6 to 323.1 mm, were measured compared to those obtained with PCE. Nevertheless, the higher dispersion strength of PCE leads to castables with a lower relative yield stress (Figure 6) and a lower relative viscosity (Figure 7). This results in lower maximum 3D slump-flow values for PMA than for PCE, despite the higher water content of castables dispersed with PMA (in combination with citric acid).
-
-
At low specific surface areas of the matrix of 1.0 and 1.3 m2/g, model castables dispersed with S-TPP (N25-15) and citric acid exhibit lower maximum 3D slump-flow values than those dispersed with PCE or PMA (in combination with citric acid). As indicated in Figure 6 (most of these castables could not be measured with the building material rheometer with spherical measuring geometry, see explanation under Section 3.3), these castables show higher relative yield stress compared to those dispersed with PCE or PMA, which may explain the considerably lower slump-flow values. As the specific surface area increases (2.7 to 4.5 m2/g), the maximum 3D slump-flow remains relatively constant, but drops at 4.7 m2/g. The explanation is the same as for PCE and PMA: increasing interparticle forces at higher matrix surface areas [9] lead to an increase in both the relative yield stress (Figure 6) and relative viscosity (Figure 7), resulting in reduced slump-flow. For the castable 4.7 m2/g with 0.010 wt.% citric acid, no slump-flow value could be determined, as the castable stiffened immediately after mixing (see explanation under Section 3.3).
In the case of PCE (Castament FS60), no clear trend in the maximum 3D slump-flow can be identified with varying concentrations. For PMA (Darvan 7S), the results remain inconclusive. Lower PMA contents are associated with higher maximum 3D slump-flow values. For S-TPP (N25-15), higher citric acid concentrations lead to an increase in maximum 3D slump-flow. This behaviour is consistent with the observed reductions in relative yield stress (Figure 6) and relative viscosity (Figure 7) at higher citric acid contents.
For almost all refractory castables with a specific surface area of the matrix of 3.0 m2/g (PCE, PMA, and S-TPP), the maximum 3D slump-flow is slightly higher than for castables with a specific surface area of 2.7 m2/g. The higher castable temperatures of 3.0 m2/g compared to 2.7 m2/g (Figure 3, see explanation for the differences in castable temperatures under Section 3.2) slightly reduce the relative yield stress (Figure 6) and relative viscosity (Figure 7) [18,19,31,36]. This could explain the marginally increased values for the maximum 3D slump-flow. Regardless of the dispersing agent system used, temperature differences can act as disturbance variables, as castable temperatures (induced by the mixing process) may influence rheological properties [18,19,31,36] and, consequently, the flow behaviour observed in slump-flow measurements (processing).
4. Conclusions
The rheological behaviour and processing characteristics of six systematically modified, self-flowing, high-alumina, CA-cement containing model refractory castables with a maximum grain size of 6 mm were investigated. For this purpose, the matrix fraction (particle sizes ≤ 45 µm) was tailored by adjusting the particle size distribution (PSD) and, consequently, the specific surface area (SSA). Highly sintered and (very) finely milled Al2O3 raw materials with high specific surface areas were employed. Three different dispersing agent systems, polycarboxylate ether (PCE, Castament FS60), polymethacrylate (PMA, Darvan 7S combined with citric acid), and sodium tripolyphosphate (S-TPP, N25-15 combined with citric acid), were applied at varying concentrations. The effects of potential overdosing of dispersing agents were outside the scope of this study and therefore not investigated. The objective was not to identify the best-performing refractory castable but rather to examine a wide range of castables with extreme matrix compositions representing very low and very high specific surface areas of the ceramic matrix in order to reveal individual effects.
4.1. Rheological Behaviour of the Matrix Suspensions
The dynamic viscosities of the matrix suspensions with the dispersing agent Castament FS60 (PCE) are dependent on the SSA, concentration, and shear rate. Suspensions with low SSA of the matrix (1.0 m2/g) display shear thickening behaviour and higher dynamic viscosities when the shear rates are increased. In contrast, suspensions with a higher SSA of 2.7 m2/g tend to exhibit pseudo-Newtonian behaviour (probably due to the overlap of shear thinning and shear thickening behaviour) over the considered shear rate range, which can be attributed to their multimodal matrix composition, and thus a broad PSD. Suspensions with a high SSA (4.7 m2/g) exhibit high dynamic viscosities (at low shear rates) and a shear thinning behaviour. However, when the shear rate is increased, a notable decline in dynamic viscosity occurs. Preliminary comparisons among the dispersing agents revealed that PMA and S-TPP result in lower dynamic viscosities compared to PCE, with the higher water demand playing a central role [7]. With PMA and S-TPP, a higher water content must be used due to a reduced dispersion strength in comparison to PCE. Dispersing agents act by overcoming interparticle forces, which are particularly pronounced at low shear rates. Consequently, a more effective dispersing agent reduces the water demand required to achieve flowability by reducing yield stress. At higher shear rates, however, interparticle forces are largely disrupted, reducing the influence of a less efficient dispersing agent. As a result, significantly lower viscosities can be achieved at higher water contents, even though the slump-flow is lower compared to castables with less water but more efficient dispersing agents.
4.2. Rheological Behaviour of the Castables
Rheological investigations of the model refractory castables (based on regression of experimental data obtained with a building material rheometer using a spherical measuring geometry and fitted with the Herschel-Bulkley model) demonstrate a clear correlation between rheological behaviour and the SSA of the matrix. At a low SSA (1.0 and 1.3 m2/g), shear thickening behaviour (n > 1) occurs, caused by the interlocking of coarse particles (with a low SSA) in the matrix under shear stress. This is accompanied by very low relative yield stress and moderate relative viscosity. Castables with an intermediate SSA of 2.7 and 3.0 m2/g (2.7 m2/g also has the broadest PSD) exhibit moderate relative yield stress and low relative viscosity. It is highly probable that both shear thinning and shear thickening behaviour occur simultaneously within the considered shear rate range due to the higher SSA and the multimodal composition (leading to a broader PSD), resulting in Bingham behaviour (with low yield stress) (n ≈ 1). Castables with high SSA values (4.5 and especially 4.7 m2/g) show shear thinning behaviour (n < 1), characterised by (very) high relative yield stress and (very) high relative viscosity at low shear rates, which can be attributed to pronounced interparticle forces (present in this low shear rate range).
PCE, as a dispersing agent, exhibits superior dispersion properties (even at very low concentrations) compared to PMA in combination with citric acid and S-TPP with citric acid. Despite the reduced water content due to its higher dispersion strength, castables dispersed with PCE exhibit low relative yield stress and relative viscosity. These findings confirm the distinct dispersion mechanisms associated with different dispersing agent systems.
The identified trends correlate with the dynamic viscosity values of the corresponding matrix suspensions in the low shear rate range. These measurements appear to provide an effective qualitative indication of the rheological behaviour of the fully composed refractory castables.
A definite influence of dispersing agent concentration on the rheological properties (in the very low shear rate range) could not be identified. However, previous studies have shown that the dispersing agent concentration has a pronounced impact on other properties of refractory castables, such as the mixing process (very high shear rates) [7] and the initial stiffening and setting behaviour [8].
Castable temperatures can influence both the relative yield stress and the relative viscosity. This effect has been reported in the literature [19,31,36] and is confirmed by the present results. The view that temperature primarily influences only the yield stress, without influencing viscosity [37], could not be confirmed. Thus, higher castable temperatures, for example, induced by mixing, may act as a disturbance variable and hinder the identification of clear trends in relative yield stress and relative viscosity. Nevertheless, the dominant factor influencing rheology appears to be the SSA of the matrix.
4.3. 3D Slump-Flow of the Castables (Processing)
3D slump-flow tests were performed to evaluate the flow behaviour of the castables, while rheological measurements were used to interpret the results and provide insights into their processing characteristics. For all dispersing agent systems considered (primarily PCE and PMA) increasing the SSA of the matrix resulted in a pronounced reduction in maximum 3D slump-flow, due to stronger interparticle forces. Castables with low SSA of the matrix (1.0 and 1.3 m2/g) exhibited high maximum 3D slump-flow values, correlating with very low relative yield stress. Castables with an intermediate SSA of 2.7 and 3.0 m2/g (2.7 m2/g also having the broadest PSD) displayed moderate maximum 3D slump-flow values and good workability. Model castables with the highest SSA (4.5 and especially 4.7 m2/g) showed the lowest maximum 3D slump-flow, consistent with their (very) high relative yield stress and (very) high relative viscosity.
However, variations in castable temperature must be considered as a source of disturbance, as they influence relative yield stress and relative viscosity, and thus the slump-flow behaviour (processing).
These results demonstrate that examining the flow behaviour of refractory castables solely on the basis of slump-flow measurements can be misleading, particularly for applications such as pumping. Castables exhibiting high slump-flow values might appear suitable, yet their pronounced shear thickening behaviour renders them entirely inappropriate for such processing techniques. In these cases, a more detailed rheological characterisation is essential to adequately evaluate the material’s performance.
Trends observed in 3D slump-flow measurements are consistent with the rheological parameters of fully composed castables as well as with the dynamic viscosity of the corresponding matrix suspensions at very low shear rates. The rheological behaviour of the matrix suspensions provides a qualitative prediction of the flow behaviour and processing properties reflected in the 3D slump-flow.
Measurements show that using PCE instead of PMA (in combination with citric acid) or S-TPP (with citric acid) leads to higher maximum 3D slump-flow values of the castables. This effect occurs even at lower water contents in the castables, due to the stronger dispersion strength of PCE, highlighting both its superior performance (even at very low concentrations) and the distinct modes of action of the different dispersing agent systems.
4.4. Matrix Rheology as an Indicator of Castable Flow Behaviour
In building materials technology, modelling the rheological behaviour of concretes through the properties of their matrix suspensions is a well-established approach [26,28,29,31]. In cement chemistry, in particular, paste-like suspensions are measured to infer the flow behaviour of mortars and concretes. In the field of refractory materials, this procedure is also applied [27,30], although it is less common, with slump-flow tests or building material rheometers being widely used. This study relates dynamic viscosity trends from matrix suspensions to rheological parameters of fully composed refractory castables, derived from Herschel-Bulkley regression analysis of experimental measurement data, obtained using a building material rheometer with a spherical measuring geometry. The observed high degree of qualitative agreement highlights that changes in the SSA of the matrix are consistently reflected in both systems, thereby underlining the central role of the matrix’s SSA in controlling the rheology and processing behaviour of refractory castables. This indicates that characterising matrix suspensions can also contribute valuable insights into the rheological behaviour and processing characteristics of fully composed refractory castables. In the present work, only the matrix composition was varied, while coarse aggregates remained constant. Nevertheless, their influence must be considered for a more comprehensive understanding of castable rheology. Methodological approaches from concrete technology can be effectively transferred to refractory castables, complementing earlier studies and advancing the state of the art in rheological characterisation.
Statement of the Use of Generative AI and AI-Assisted Technologies in the Writing Process
During the preparation of this manuscript, the authors used DeepL SE in order to enhance the linguistic quality. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the published article.
Author Contributions
Conceptualization, F.H., T.W., J.K., C.D., O.K.; Methodology, F.H.; Validation, F.H., T.W., J.K.; Investigation, F.H.; Data Curation, F.H.; Writing—Original Draft Preparation, F.H.; Writing—Review & Editing, F.H., J.K., T.W.; Supervision, J.K., C.D., O.K.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
Funding
This research project has been supported by the Federal Ministry for Economic Affairs and Energy (BMWE) on the basis of a decision by the German Bundestag.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
-
Dinger DR, Funk JE. Particle Packing, Part II—Review of Packing of Polydisperse Particle Systems. Interceram 1992, 41, 176–179. [Google Scholar]
-
Dinger DR, Funk JE. Particle Packing III—Discrete versus Continuous Particle Sizes. Interceram 1992, 41, 332–334. [Google Scholar]
-
Funk JE, Dinger DR. Particle Packing VI—Applications of Particle Size Distribution Concepts. Interceram 1994, 43, 350–353. [Google Scholar]
-
Fruhstorfer J, Aneziris C. The influence of the coarse fraction on the porosity of refractory castables. JCST 2014, 5, 155–166. [Google Scholar]
-
Bayoumi IMI, Ewais EMM, El-Amir AAM. Rheology of refractory concrete: An article review. BoletÍN de la Soc. Española de CerÁMica y Vidr. 2022, 61, 453–469. [Google Scholar]
-
Kockegey-Lorenz R, Buhr A, Zacherl D, Long B, Hayashi S, Dutton J. Review of Matrix Aluminas for Refractory Formulations. In Proceedings of the UNITECR2011, Kyoto, Japan, 30 October–2 November 2011; pp. 789–794. [Google Scholar]
-
Holleyn F, Waldstädt T, Kasper J, Ibarra Plata LT, Dannert C, Krause O. Effects of changing the specific surface area in the ceramic matrix of CAC-containing refractory castables on the dispersion and mixing process. J. Ceram. Sci. Technol. 2025, 16, 173–185. doi:10.4416/JCST2024-00023. [Google Scholar]
-
Holleyn F, Waldstädt T, Kasper J, Dannert C, Krause O. Effects of changing the specific surface area in the ceramic matrix of CAC-containing refractory castables on the initial stiffening and setting behaviour. High-Temp. Mater. 2025, 2, 10009. doi:10.70322/htm.2025.10009. [Google Scholar]
-
Schnabel M, Buhr A, Dutton J. Rheology of High Performance Alumina and Spinel Castables. Refract. Worldforum 2012, 4, 95–100. [Google Scholar]
-
Heinrich J. Formgebung in der Keramik. In Salmang-Scholze-Telle; Springer: Dodrecht, The Netherlands, 2007; pp. 568–623; ISBN 3-540-63273-5. [Google Scholar]
-
Plank J, Sachsenhauser B. Impact of Molecular Structure on Zeta-Potential and Adsorbed Confirmation of α-Allyl-ω-Methoxypolyethylene Glycol-Maleic Anhydride Superplasticizer. J. Adv. Concr. Technol. 2006, 4, 233–239. [Google Scholar]
-
Plank J, Bassioni G, Dai Z, Keller H, Sachsenhauser B, Zouaoui N. Neues zur Wechselwirkung zwischen Zementen und Polycarboxylat-Fließmitteln. In Proceedings of the 16th Internationale Baustofftagung ibausil, Weimar, Germany, 20–23 September 2006; pp. 579–598. [Google Scholar]
-
Kasper J. Modellbildung zum Abbindeverhalten von PCE-verflüssigten und CA-Zement-Gebundenen Feuerbetonen. Doctoral Dissertation, Universität Koblenz-Landau, Koblenz, Germany, 2021. [Google Scholar]
-
Sachsenhauser B. Kolloidchemische und Thermodynamische Untersuchungen zur Wechselwirkung von α-Allyl-ω-Methoxypolyethylenglykol-Maleinsäureanhydrid-Co-Polymeren mit CaCO3 und Portlandzement. Doctoral Dissertation, Technische Universität München, Munich, Germany, 2009. [Google Scholar]
-
Ferraris CF. Measurement of the rheological properties of high performance concrete, state of the art report. J. Res. Natl. Inst. Stand. Technol. 1999, 104, 461–478. [Google Scholar]
-
Justnes H, Vikan H. Viscosity of cement slurries as a function of solids content. Annu. Trans. Nord. Rheol. Soc. 2005, 13, 75–82. [Google Scholar]
-
Silva AP, Segadães AM, Pinto DG, Oliveira LA, Devezas TC. Effect of particle size distribution and calcium aluminate cement on the rheological behaviour of all-alumina refractory castables. Powder Technol. 2012, 226, 107–113. [Google Scholar]
-
Mezger TG. Das Rheologie Handbuch: Für Anwender von Rotations-und Oszillations-Rheometern, 5th ed.; Vincentz Network: Hannover, Germany, 2016; ISBN 978-3-74860-012-1. [Google Scholar]
-
Uebachs S. Charakterisierung und Modellierung des Fließverhaltens von selbstverdichtendem Beton. Doctoral Dissertation, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2016. [Google Scholar]
-
Elfering M. Experimentelle Strömungsanalyse Im Gerührten Fermenter. In Forschungsreihe der FH Münster; Springer: Wiesbaden, Germany, 2018; ISBN 978-3-658-22485-1. [Google Scholar]
-
Magnon E, Cayeux E. Precise Method to Estimate the Herschel-Bulkley Parameters from Pipe Rheometer Measurements. Fluids 2021, 6, 157. [Google Scholar]
-
Haist M, Link J, Nicia D, Leinitz S, Baumert C, Von Bronk T, et al. Interlaboratory study on rheological properties of cement pastes and reference substances: Comparability of measurements performed with different rheometers and measurement geometries. Mater. Struct. 2020, 53, 92. [Google Scholar]
-
Kockegey-Lorenz R, Schmidtmeier D, Buhr A, Dutton J. E-SY Alumina for Easy to Use High-Performance Castables. In Proceedings of the 52nd ICR, Aachen, Germany, 23–24 September 2009; pp. 86–88. [Google Scholar]
-
Büchel G, Buhr A, Aroni J, McConnell R. E-SY Pump—The New Solution for Pumpability of Silica Free High Performance Tabular Alumina and Spinel Castables. In Proceedings of the 47th ICR, Aachen, Germany, 13–14 October 2004; pp. 87–90. [Google Scholar]
-
Ortega F, Pileggi R, Studart A. IPS A Viscosity—Predictive Parameter. Am. Ceram. Soc. Bull. 2002, 81, 44–52. [Google Scholar]
-
Ferraris C, Obla K, Hill R. The influence of mineral admixtures on the rheology of cement paste and concrete. Cem. Concr. Res. 2001, 31, 245–255. [Google Scholar]
-
Otroj S, Bahrevar MA, Mostarzadeh F, Nilforoshan MR. The effect of deflocculants on the self-flow characteristics of ultra low-cement castables in Al2O3-SiC-C system. Ceram. Int. 2005, 31, 647–653. [Google Scholar]
-
Lange A. Studien zur Zementkompatibilität von Polycarboxylat-Fließmitteln sowie zum Einfluss ihres HLB-Wertes auf das rheologische Verhalten von Mörteln. Doctoral Dissertation, TU Munich, Munich, Germany, 2015. [Google Scholar]
-
Han D, Kim JH, Lee JH, Kang S-T. Critical Grain Size of fine Aggregates in the View of the Rheology of Mortar. IJCSM 2017, 11, 627–635. [Google Scholar]
-
Bastian M, Kasper J, Dannert C, Pokhrel A, Ibarra Plata LT, Krause O. Measurement of the Dynamic Viscosity of Refractory Castables—Interaction between Slurry and Aggregates. In Proceedings of the 65th ICR, Aachen, Germany, 28–29 September 2022; pp. 53–56. [Google Scholar]
-
Gołaszewski J, Cygan G. Influence of temperature on rheological properties of self-compacting mortars and concretes in rest state. Arch. Civ. Eng. 2024, 70, 255–269. ISSN 1230-2945. [Google Scholar]
-
Zhou X, Sankaranarayanane K, Rigaud M. Design of bauxite-based low-cement pumpable castables: A rheological approach. Ceram. Int. 2004, 30, 47–55. [Google Scholar]
-
Krause O, Pokhrel A, Ibarra Plata LT, Kakavand M, Bastian M, Linden C, et al. Rheology of Refractory Castables—Part 1: A Novel 3D Spread Flow Measuring Device Allows to Determine More Precisely the Workability of Refractory Castables. In Proceedings of the UNITECR 2023, Frankfurt, Germany, 26–29 September 2023; pp. 232–235. [Google Scholar]
-
Bastian M, Kasper J, Dannert C, Klein G. New Approach for the Determination of the Shear Rate Dependant Viscosity of Refractory Castables. In Proceedings of the 63th ICR, Aachen, Germany, 16–17 September 2020; pp. 52–55. [Google Scholar]
-
Kakavand M, Ibarra Plata LT, Zoch J, Krause O. Enhanced Rheological Characterisation of Vibratable Castables: A Comparative Study between Conventional Slump Tests and 3D Spread Flow Measurements. In Proceedings of the 67th ICR 2024, Aachen, Germany, 18–19 September 2024; pp. 158–161. [Google Scholar]
-
John E, Gettu R. Effect of Temperature on Flow Properties of Superplasticized Cement Paste. ACI Mater. J. 2014, 111, 67–76. [Google Scholar]
-
Schmidt W. Design Concepts for the Robustness Improvement of Self-Compacting Concrete. Doctoral Dissertation, Eindhoven University of Technology, Eindhoven, The Netherlands, 2014. [Google Scholar]