A Critical Analysis of Kinetic Models in Photocatalysis and Some Necessary Improvements
Received: 01 October 2025 Revised: 24 October 2025 Accepted: 04 November 2025 Published: 07 November 2025
© 2025 The authors. This is an open access article under the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/).
1. Introduction
Kinetic models, which are solved into equations, are used to quantitatively interpret experiments, such as the disappearance of a substrate over time under certain experimental conditions, photoluminescence experiments, transient absorption experiments, and photoelectron density experiments. Kinetic models can be used to improve certain parts of the treatment system, namely the chemical reactors used in both gas- and liquid-phase applications for the degradation of pollutants and naturally occurring dissolved organic matter [1], and eventually nanoplastics [2]. They also improve the application possibilities of the photocatalytic process, including the definition and geometry of the reactors used for this purpose, scaling up, and determining the optimal range of reagent concentrations that can be used. Furthermore, kinetic models are used to interpret and formulate hypotheses about the mechanism of chemical transformation, and therefore to select the mechanisms (e.g., improved charge separation and reduced recombination) that operate in photocatalysis under certain conditions, which may depend on the type of substrate as well as the type of catalyst.
A perfect fit of a kinetic model to the experimental data does not necessarily imply that the adopted mechanistic model is valid. “Even if a reaction mechanism generates a rate equation, i.e., an expression for the overall rate as a function of the key reactant/product concentrations, that appears to fit all the data, it does not necessarily mean it is the actual reaction mechanism” [3,4]. Conversely, if the kinetic model does not work, it is necessary to revise the mechanistic assumptions on which it is based, considering the chemical information obtained in properly designed experiments or observation of formed intermediates (see below).
Kinetic models apply only LOCALLY, that is, within an infinitesimal volume within the reactor. The reaction rate, as will be seen below, obviously depends on the concentration of the reagents and catalyst, which can be assumed to be homogeneous within a reactor, and on the local light intensity, which instead depends on the position in the reactor. The observed reaction rate (or other related quantities such as the photoelectron density) requires integration over the reactor volume of kinetic equations with the current local concentrations of reagents and light intensity. These may depend on the type of reactor used:
(1) Batch reactor. In this closed reactor, the reaction starts when illumination begins. The concentration of the reactants is monitored over time, obtaining a temporal evolution. Fitting this temporal evolution leads to the evaluation of the apparent degradation constant kobs, and consequently rate = kobs × C. In this case, the initial rate at the nominal concentration C0 at time t = 0 is evaluated by extrapolation, albeit with some risk. An example of integration performed in a one-dimensional reactor is reported [5]. Note that the integration provides the average of the reaction rates over the reactor volume, and that the integration of the absorbed light over the reactor volume cannot be used in a kinetic model (the average of the rates, which depend on the absorbed light, is not equal to the rate estimated from the average absorbed light, due to the nonlinear relationship between absorbed light and reaction rate).
(2) CST Reactor. The Continuous Stirred Reactor operates with a continuous flow of reactants at a constant concentration, so that a constant conversion η∞ is measured in a steady state. The rate is given by rate(C) = C0 η∞ F = kobs × C, where F is the (constant) flow entering the reactor. The conversion η∞ refers to the substrate concentration C at the reactor outlet, but it can easily be normalized to the inlet concentration, obtaining the rate at a given C0 [6]. It can be easily demonstrated that kobs = η∞ F/(1 − η∞). In CSTR, the experimental measure of η∞ directly gives kobs. The CSTR has numerous other advantages over the batch reactor, including that adsorptions on the catalyst, its poisoning, or its change in properties over time can be more easily detected (η∞ is not constant, so also kobs). However, the use of CSTR is mostly limited to gas/solid reactions.
From the previous considerations, it emerges that the verification, validation, or application of a kinetic model is strongly dependent on the experimental conditions for data production/acquisition. These conditions are not always sufficiently indicated in published works (illumination geometry, slurry or film thickness), making comparisons sometimes problematic. However, it remains unlikely that the validation of a kinetic model can be adequately performed by exchanging the local parameters of the kinetic model with the parameters (concentration and light intensity) applied to the reactor (except for a reactor with a thin-layer catalyst or with an infinitesimal slurry thickness, or isoactinic). This fault is almost always made in scientific literature.
In addition, the properties a kinetic model must possess are that the equations for the experimental variables (for example, for the rate) must be as simple as possible, and if possible, in analytical form. This means that from a general framework, even one considered very plausible, approximations made may be questionable, both based on chemical and mathematical knowledge. As a result, formulating a kinetic model is not a simple matter, especially in photocatalysis, where the system is fundamentally very complex.
2. Common Kinetic Models
Here, a critical analysis of the two main kinetic models will be performed, following a logical and chronological line, as they have been proposed, implemented, and modified over time by various research groups. The enormous literature supporting the formulation of kinetic models is not cited in detail. Then, please check the references cited in the papers here.
This analysis is not intended to replace the extensive review by Mills [3], in which 10 major models were reviewed. Mills et al. made a great and invaluable effort to unify notations and correct errors in the original papers. They classified the models as: (1) Langmuir: Ollis Langmuir (case III; ER mechanism); Emeline (Langmuir mechanism), Salvador (Direct Transfer, DT mechanism); Ollis disrupted adsorption model (non-equilibrated adsorption where rate = αϕθ[A], and 0.5 ≤ θ ≤ 1 is an arbitrary parameter); (2) Quadratic: Gerischer; Salvador (indirect transfer, IT mechanism); Marin (quadratic with back reaction, (2011) following Minero [7]); (3) Combined: Salvador (IT and DT combined), Revised Ollis disrupted adsorption model, DT modified Ollis disrupted adsorption model (non-equilibrated adsorption model). For various models, see references in the Mills paper [3]. All these kinetic models have some common characteristics: they consider the recombination rates of the photogenerated species (kr[h+][e−], kr[OH•/hs+][e−], kr[hs+][e−], where the subscript “s” indicates a surface species), trapping is somehow considered (hs+) as a generic surface trap, the photogenerated species react with the substrate (A, reduced) and an oxidant (B, generally oxygen, so B is generally just an electron scavenger whose rate is kB[e−][B]). The resulting kinetic equations are in the form of a Langmuir type or as square roots (called quadratic models due to the solution of a second-order equation in [e] or [h]), which predict a monotonically increasing saturative shape. It is anticipated here that not all experimentally observed rates can be rationalized.
The models have been compared by Mills et al. [3] considering the good of quality fit in the existing literature database for the rate([A],ϕ) over a limited range of substrate concentrations and light intensities for different substrates. They concluded that the best model, in terms of overall fit, simplicity, usefulness, and versatility, is the disrupted adsorption kinetic model proposed by D.F. Ollis [8]. It is noteworthy that in this model, a step is present in which the trapped hole can oxidize something in addition to the substrate at a constant rate, which could be water oxidation (later referred to here as khw × [h]). In this model, the photocatalytic process rate of consumption of A, whether in solution or adsorbed on the surface, is greater than that of the adsorption and desorption processes, so that reactant adsorption is not equilibrated. This assumption can be demonstrated by the reduction of a full kinetic system (here not reported), in which it is evident that the equilibrium assumption is valid only when other reactions are very slow. Mills at al. also revised this original model (see #9 in Appendix B of [3]). Other models, including quadratic models, have similar fit qualities. However, this type of analysis is misleading, as kinetic models are local models that require integration over the experimental reactor adopted. Therefore, since experimental rates are mean (integral) values, they cannot be directly compared to kinetic model equations, unless these are integrated on the actual reactor configuration. Consequently, rather than accepting a model with a similar fit, we prefer to discuss the validity of the assumptions underlying the kinetic model itself.
The first fully developed kinetic model was proposed by Ollis (1983) [9,10]. For halogenated hydrocarbons examined, the initial rate of reaction vs. reactant concentration was satisfactorily shown by a Langmuirian shape with a slow surface reaction step, according to rate = k × {A}, where {A} is the adsorbed A given by a Langmuir isotherm {A} = , KA is the apparent binding constant of A on the illuminated catalyst, and [A] is the concentration in the solvent. This law was later heavily criticized because the adsorption constants under light do not correspond to those in the dark (see, for example, an extensive discussion with the original references in [4,11]).
From this preliminary observation, it is evident that A (reduced species), whether free or adsorbed, must react with a photogenerated species, called for now ‘h’ (it could be hole or a surface-trapped hole, in the following the concentrations of eCB, and h+VB are indicated simply by [e] and [h]), so
Starting from the observation of Cunningham et al. [12] on H2O/D2O kinetic isotope effect, in which they observed that replacing the H2O solvent with D2O led to a decrease in rate, and which therefore suggested that the rate-limiting reaction step is the formation of active species through reactions involving the solvent (OH or OD), Turchi and Ollis (1990) assumed that the reactive species generated in photocatalysis was h = OH [13]. In the scientific works of those years, the same assumption was often made. This belief is still rooted in literature, even if, as will be seen below, the assumption of these reactive species is not always justified. Obviously, it remained to be defined in the model how [h] was related to the rate of light absorption. Considering the generation of reactive species, adsorption, recombination and possible trapping, they analyzed four possible cases of reaction of OH with A under steady-state conditions: (I) Reaction occurs while both species are adsorbed (LH, Langmuir Hinshelwood mechanism); (II) A nonbounded radical reacts with an adsorbed organic molecule (ER, Eley Rideal mechanism); (III) An adsorbed radical reacts with a free organic molecule arriving at the catalyst surface (ER); (IV) Reaction occurs between two free species in the fluid phase. They concluded that the rate equation is of the form given in Equation (2), the appearance of which is the familiar Langmuir-Hinshelwood kinetic rate law, irrespective of which of the four cases is considered (see above, the kinetic model does not ensure the mechanism).
where kobs is linear dependent on ϕ at low ϕ and on ϕ1/2 at high ϕ (given as two different formulas as limiting cases), and κ depends on [sites] and different microkinetic constants according to the case (I–IV) above considered. The fate of oxygen (B) has not been explored in the development of this rate law. They derived the above equation assuming [h] = [e].
This strong boundary condition ([h] = [e]) has been abandoned in quadratic models (QM) [5,14,15], where it turns out that [h] is proportional, not equal, to [e], and their relative concentrations depend on the concentrations [A] and [B]. The rate is always given by Equation (1). The concentrations of photogenerated species [h] and [e] are obtained by solving the following (new) system of two equations in steady state, where Rh = d[h]/dt = 0 and Re = d[e]/dt = 0. In the original published formulation, the quantities in {} are not present, and are introduced here for the purposes of discussion below.
where in the rh terms βh = kha[A] + {khw} and βe = keb[B] + {kea[A] + kew};
and where [A] and [B] are the concentrations at the catalyst surface on which the reaction necessarily occurs [16]; ϕ is the rate of light absorption by the catalyst and generation of charge carriers [5]. This depends on the catalyst concentration Ccat, the intensity of the incident light, and, especially for slurries, on how much light is lost through scattering. It is a parameter that is usually unknown and not easily measurable [5,17,18]; kha[h][A] is the oxidation rate of A, khw[h] is the oxidation rate of the solvent (possibly to yield OH or OHads, according to [8]), keb[e][B] is the reduction rate of the oxidant B, kew is the reduction rate of the solvent or catalyst sites (i.e., Ti(IV)→Ti(III to produce blue TiO2)), kea[e][A] is the reduction rate of the substrate A. These last two contributions can be negligible in the presence of effective electron scavengers.
The model here proposed is therefore a generalized quadratic model (QMG) that reduces to the QM model in the absence of the terms in {}, i.e., for kew = 0, khw = 0, and kea = 0. The QMG model can therefore be applied also to a series of substrates not contemplated in QM (kea 0), for example, those that can be reduced or simultaneously oxidized and reduced, as is the case of halophenols [19,20]. This application is not further developed here. The solution for [h] is obtained by the difference Re − Rh (both being = 0 in steady state). It is observed that [h] is proportional to [e], and depends also on the concentrations of the species in the system.
The solution for [e] is obtained by introducing [h] in Re = 0 (see Equation (3)) and solving the resulting quadratic equation. The IT rate expression developed by Salvador et al. [21,22] is identical mathematically to that of the quadratic model QM.
The rate (in the case of a species that is only oxidizable, for which kea = 0) is rate = [h]*βh (see below for the justification of this expression) and therefore is given by
where β0 = βe βh/(2 kr).
This is an expression with only TWO lumped parameters (ϕ and β0, already reported in the left form expressed here [11]), which shows how the rate has an almost Langmuirian behavior (with the square root of β0, hence again the name quadratic model), even in the absence of an explicitly expressed Langmuir isotherm for [A] and/or [B]. We also note that rate = 0 for ϕ = 0 and for kr = ∞, and rate = ϕ for β0 = ∞ (either βe = ∞ or βh =∞), as expected.
The dependence of the rate on β0 and ϕ according to Equation (5) is reported in Figure 1, which describes all the characteristics of the QMG model (and obviously of QM, which is a particular case of it, for which β0 = kha keb [A] [B]/(2 kr)). The rate depends: (1) linearly on ϕ (i.e., ϕ1 ) at small ϕ values (always, see the bottom part of the figure) and for any value of ϕ if β0 is sufficiently large (see the right part of the figure); (2) with the square root of ϕ (i.e., ϕ1/2 ) for β0 values sufficiently small and ϕ large; (3) it is independent of β0, i.e., on the concentrations of [A] and [B], for small ϕ (bottom part of the figure); (4) it depends on β01/2 for small β0 and large ϕ (top left part of the figure); (5) it is independent of β0, i.e., on the concentrations of [A] and [B], for large ϕ (top right part of the figure) where a saturation trend is observed.
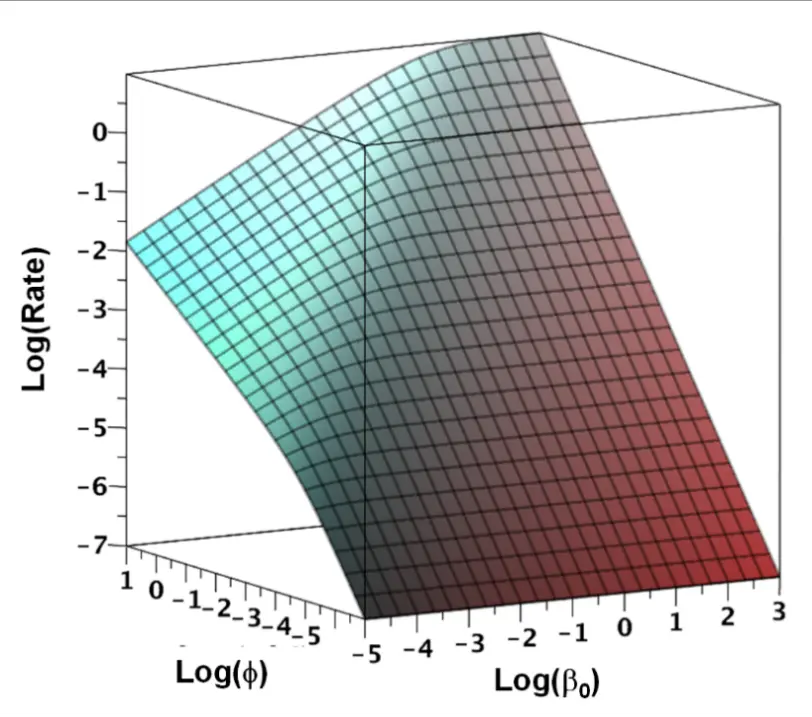
Figure 1. Logarithmic plot of the dependence of the rate on lumped parameters β0 and ϕ. β0 increases as [A] and [B] increase. ϕ increases with the catalyst concentration and the intensity of the light.
From an experimental point of view, the rate obtained from QMG (or QM) model can be compared (apart from the integration of the rate over the reactor volume, which depends nonlinearly on the absorbed light ϕ(x,y,z), mentioned above) directly with the rate or with the observed degradation kinetic constant kobs, since kobs = rate([A],[B])/[A]. The QM has been extensively validated, both for estimating rates in solution [5,23] and for degradation in gas/solid systems [24]. In this last work, it was demonstrated that the predictions of the QM model justify well the increase in the observed degradation kinetic constants when the gas-phase concentration is reduced from parts per million (ppm) to parts per billion (ppb).
In summary, the QM model well explains the dependence on light intensity with an order of 1/2 up to 1, and the dependence on substrate concentration with an order of 1/2 up to 0.
3. Chemical Support of Different Kinetic Mechanisms
The QM model is almost silent on possible microscopic mechanisms, which is in agreement with the findings of Ollis (see above), since it deliberately uses a few kinetic constants that embody possible different kinetic pathways not explicitly defined or expressed, as they do not distinguish between bulk or surface photogenerated charges.
A more plausible kinetic scheme is the one shown in Figure 2.
It is based on conclusions of an experiment on the degradation of decafluorobiphenyl (DFBP) with TiO2, which is slow in the presence of Al2O3, on which it adsorbs tenaciously: “Active species formed upon irradiation do not migrate in solution, while the organic substrate may or may not migrate to the catalyst surface. Only when both are present at the catalyst surface does the degradation take place” [16]. Thus, if the reaction is confined to the catalyst surface, three possible mechanisms can coexist. An extensive discussion of these mechanisms and related literature is reported elsewhere [25]. The scheme in Figure 2 also serves to give explicit names to the different mechanisms, which are sometimes confused in the literature.

Figure 2. A detailed kinetic scheme for primary events at the surface of a photocatalyst. The species with (*) are radicals. Charges of species are omitted.
This kinetic scheme explicitly considers that the charge transfer (ET) reaction can occur: (1) at the surface through an oxidized S site (S0*, equivalent to a surface-trapped h+) with an outer sphere (or indirect) ET mechanism, which is equivalent to an ER mechanism; (2) with an inner-sphere (or Direct) mechanism on the adsorbed species AS; (3) when the species S0* can react with the (adsorbed) solvent to produce a further reactive species R0. A similar kinetic scheme is also applicable to the oxidant species B, which must be coupled to the scheme in Figure 2 by replacing A, AS, AS0, AO* with B, BS (B bound at the surface), BSR (BS reduced at the surface), and products of B reduction, respectively. The analysis of the overall kinetic scheme is challenging to reduce to simple kinetic equations, as it involves many parameters and balances the activity of numerous surface sites. A possible analysis will be reported in future work. In this work we continue to consider the role of oxidant B as a pure electron scavenger, with a rate keb [e] [B] as assumed in Equation (3). A pictorial view of surface sites is reported in Figure 3.

Figure 3. Pictorial view of surface site S, the oxidized surface site S0*, and the adsorbed oxidized substrate AS0*.
The following section explains the meaning of the various kinetic pathways and provides experimental support for this detailed kinetic scheme.
(1) Mediated mechanism. The free surface S site can trap holes and be oxidized (S0*), and as such, it can function as a site for the recombination of electrons in the conduction band. The recombination mediated by surface traps is a reasonable possibility for indirect semiconductors, because direct recombination in the bulk is not permitted for indirect semiconductors such as TiO2 [26]. From the perspective of the QM model, [h] corresponds to [S0*] and ke1 (in the Scheme of Figure 2) to kr. This implies that the QM model implicitly assumes rapid surface trapping of holes produced in the bulk. This assumption is not unlikely, since charge carrier generation occurs at or near the surface, where most of the light is absorbed.
The S0* site can react alternatively with A (ER mechanism, see below the case 2) or with the adsorbed solvent with kinetic constant khw, to generate the reactive species R0 that can eventually later react with A. This last kinetic pathway is not present in the QM model, whereas it is reported in the above described QMG model through the term khw [h]. This assumption remedies a strong weakness of the standard QM model, in which for β0 = 0 (i.e., when khw = 0 and kew = 0 for [A]→0 or [B]→0), the rate is null.
Various experimental results of this research group (unpublished but collected over 20 years) show that the reaction rate for different substrates does not tend to zero for [A]→0. Two cases are reported in Figure 4. It is noted that for formic acid, the rate increases with concentration, while for catechol, it decreases. In this last case, the discussion of which is outside the scope of this work, the strong recombination of the oxidized species with photoelectrons can be invoked due to the strong adsorption of catechol on TiO2.

Figure 4. Dependence of the rate on a large set of substrate concentrations for formic acid and cathecol (Minero C. unpublished data obtained on TiO2 P25 under the same conditions).
Here, attention is focused on the rate at very low concentrations. From the above data, it seems that the limit for the rate when [A]→0 is not only non-zero but is also independent of the type of substrate. This observation is adequately resolved with the QMG model, which introduces the reaction khw*[S0*]→R0 (see the Scheme of Figure 2), where R0 is a reactive oxidizing species that can further react with A. In fact, if we consider R0 + A → PA with constant kRo with [S0*] in steady state, d[R0]/dt = khw × [S0*] − kRo × [R0] × [A] = 0, so the mediated degradation rate Rm = d[A]/dt = kRo × R × [A] = khw × [S0*], depends on [S0*],(h trapped), but is independent of [A], and therefore of both its concentration and the type of substrate. Then the rate is not null in the limit [A]→0. This also implies that a linear decrease in [A](t) must be observed with the irradiation time t.
The data reported in Figure 4 provide strong experimental evidence supporting the mediated mechanism at low substrate concentration. The R0 species can be identified in free OH (unlikely, see ref. [11]), or in surface species other than S0* produced by reaction with the solvent through a surface modification of the catalyst, as reported [27]. This (mediated) mechanism is always active if [S] is not null, in parallel with the indirect and direct mechanisms (see below).
(2) Indirect mechanism. The oxidized surface site S0* is the site of the outer sphere (indirect) substrate oxidation reaction. The equivalent in the QM model is that [h] → [htrapped] so that [h] corresponds to [S0*] and k1p → kha. This kinetic path, also possibly in addition to the mediated path (1), is followed when the substrate A does NOT adsorb on the catalyst (due to properties of the substrate, and then only physisorption is allowed) or CANNOT be adsorbed on S, because the site is occupied by a more adsorbed ligand. This latter case is observed for a fluorinated surface where S→SF. In these two cases, the reaction follows the Eley-Rideal mechanism (ER), the already cited Ollis mechanism (III), where an adsorbed radical reacts with a free organic molecule arriving at the catalyst surface. The rate is given in the QM model by kha × [h] × [A], where [h]→[htrapped] = [S0*], which implies an exponential decay of [A](t) with the irradiation time t. Experimental evidence that this mechanism exists (and not only the OH-mediated mechanism) was provided by degradation experiments of melamine, which is poorly adsorbed on TiO2 [28]. Melamine is inert toward OH radicals (H abstraction) because both H2O2/UV (254 nm) and Fenton reagent (H2O2 0.1 M, [Fe2+] 0.1 M, pH 2–6) do not degrade it. Melamine (E° 1.9–2.3 V vs. NHE) is oxidized on P25 and by S2O82−/h+, confirming that the operating mechanism is electron abstraction (TiO2/h+ > 2.8 V S2O82−/hν $$\boldsymbol{\cong}$$ 2.4 V). Melamine is degraded at the same rate on P25 or fluorinated P25. This demonstrates that the ER mechanism operates in photocatalysis.
Both mechanisms are contemplated in the QMG model. It follows that the rate dependence rate(ϕ,β0) is still that reported in Figure 1, considering that β0 cannot be zero even for [A] = 0 (in this case β0 = (kha[A] + khw) βe/(2 kr)). Therefore, the rate always shows a monotonic increasing trend with [A] starting from a value β0 = khw βe/(2 kr) (see left limits indicated in Figure 4). The developed QMG model does not consider the third pathway (Direct) depicted in Figure 2 implying adsorbed AS.
(3) Direct ET. The site S has the explicit possibility of adsorbing the substrate A with forward and reverse rates, k1a and k1b, respectively. In the kinetic model, it can be assumed that the equilibrium Keq = k1a/k1b does not hold as in the adsorption kinetic model proposed by D.F. Ollis [4,8]. The adsorbed species AS can trap holes and be oxidized (AS0*), and as such can function as a site for electron recombination (substrate-mediated recombination, originally introduced as a back reaction [7]). Possible photoadsorption pathways, i.e., the reaction A + S0*![]() AS0*, are not considered in the kinetic scheme. The photoadsorption pathway, discussed in the early literature, leads to the same surface complex AS0* and can be kinetically redundant. The adsorption of A to form the surface complex AS adds a third possible kinetic pathway (called Direct, DT), which is operative when the substrate A can adsorb onto the catalyst (due to substrate properties, chemisorption). In this case, this mechanism is competing with the ER mechanism. When adsorption occurs, the concentration of free surface sites [S] decreases, so the relative weights of the Mediated and IT paths are reduced. A combined mechanism was proposed (e.g., Salvador IT and DT combined [22]).
AS0*, are not considered in the kinetic scheme. The photoadsorption pathway, discussed in the early literature, leads to the same surface complex AS0* and can be kinetically redundant. The adsorption of A to form the surface complex AS adds a third possible kinetic pathway (called Direct, DT), which is operative when the substrate A can adsorb onto the catalyst (due to substrate properties, chemisorption). In this case, this mechanism is competing with the ER mechanism. When adsorption occurs, the concentration of free surface sites [S] decreases, so the relative weights of the Mediated and IT paths are reduced. A combined mechanism was proposed (e.g., Salvador IT and DT combined [22]).
Experimental evidence that the DT mechanism exists has been reported in the kinetic analysis of phenol (Ph) degradation experiments in the presence of alcohols (Al) at different [Ph]/[Al] ratios in the absence and presence of fluorides (see Figure 2 in [29]). The kinetic analysis showed that for [Ph]/[Al]$$\rightarrow$$0 the intercept gives the ratio Direct over Mediated/Indirect oxidation of phenol. It was observed that in the case of the fluorinated surface, the intercept is zero, that is, for TiO2/F the mechanism is totally mediated/indirect, while for naked TiO2 the intercept is not zero, that is, the mechanism is partially direct.
The direct electron transfer (DT) mechanism is strictly speaking a Langmuir-Hinshelwood (LH) mechanism. For a reaction carried out at the catalyst surface, it is also to be expected that the transformation products may differ from those obtained in the case of the ER mechanism (see the pictorial view of AS0* in Figure 3). The proof of LH was clearly evidenced in the experiment of degradation of glycerol (GLY) [30]. On TiO2 Merck, P25/F, Merck/F, when adsorption is poor or impeded by fluoride adsorption, the main products observed were glyceraldehyde (GAD) and dihydroxyacetone (DHA) (C3). These products are also obtained by OH oxidation and then are produced by a mediated mechanism or oxidation by S0* (ER mechanism). Conversely, at the onset of adsorption and at larger GLY concentrations on TiO2 P25, the observed products are HCHO (C1) and glycolaldehyde (GLC, C2). HCHO and GLC can be obtained with periodate (E° 1.60 V) oxidation by concurrent bielectronic transfer, thus suggesting a concerted mechanism at the surface, probably also involving locally adsorbed/produced O2−. To my knowledge, no other such compelling evidence for an LH mechanism has been reported.
The formulation of a kinetic model that includes both the mediated (1), indirect (2), and DT (3) mechanisms is not simple. Considering AS, even with the simplifying assumption that it is in equilibrium with A ([AS] = Keq [A][S], where [A] is in this case the concentration of A in solution), implies the evaluation of [S], and therefore the site balance, and the introduction of further kinetic parameters (kh2 for oxidation and ke2 for recombination, i.e., of the substrate-mediated back reaction). It is obvious that at equilibrium [S] = Cs*(1 − θ) and [AS] = Cs* θ, where θ is the degree of coverage (given by a Langmuir isotherm) and Cs the total number of sites. This greatly complicates the kinetic model and prevents its reduction to analytical formulas. The introduction, in a generic way in a QM context, of the back reaction alone leads to third-degree polynomials in [e] [7], but is able, at least qualitatively, to justify the reduction in rate with increasing [A], as in the case of catechol in Figure 4. Therefore, much work remains to be done in developing reliable kinetic models, and above all, those that can be reduced to manageable equations.
4. Conclusions
The kinetic models can be used not only for reactor scale-up, but also as a general framework for evaluating improvements and attributing them to specific mechanisms in materials and photocatalytic reactions. The simple QMG model and almost all those reported by Mill [3] predict a rate increase with the substrate concentration. Given the dependencies of the rate in Figure 1, the experimental observation, reported in the uncountable works on the synthesis of new materials, of an increase of the rate (or related parameters such as [h] or [e] given Equation (5), for example from photoluminescence) does not necessarily implies an increase in the charge separation (a decrease in kr, as almost always assumed). The increase must be attributed: (1) to an increase in β0 (and therefore to an increase in the factors in it included, i.e.,: (a) to the mentioned decrease in kr; (b) to a possible increase in βh = kha[A] + khw, due to a possible increased specific reaction rate kha or [A] at the surface (due to chemisorption), or to an increase in khw; (c) to a possible increase in βe = keb[B] + {kea[A} + kew}, i.e., to the terms entering it; (2) to an increase in ϕ, i.e., to the rate of light absorption. This last in turn depends on the composition of the material, the size of the particles, their shape, their aggregation, and their concentration. We have shown that the dependence on ϕ is a crucial value for photocatalytic efficiency [17]. Consequently, great caution must be taken to advance mechanistic explanations from rate data.
Acknowledgments
The author acknowledges support from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027 (CUP: D13C2200352001)”.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Funding
Financial support under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 2 February 2022 by the Italian Ministry of University and Research (MUR), funded by the European Union—NextGenerationEU–Project Title Development of an operative procedure for the quantification of nanoplastics and the evaluation of their role in environmental samples—CUP 2022PN4KCS—Grant Assignment Decree No. 104 adopted on 2 February 2022 by the Italian Ministry of Ministry of University and Research (MUR).
Declaration of Competing Interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Chen D, Cheng Y, Zhou N, Chen P, Wang Y, Li K, et al. Photocatalytic degradation of organic pollutants using TiO2-based photocatalysts: A review. J. Clean. Prod. 2020, 268, 121725. doi:10.1016/j.jclepro.2020.121725. [Google Scholar]
- Surana M, Pattanayak DS, Yadav V, Singh VK. An insight decipher on photocatalytic degradation of microplastics: Mechanism, limitations, and future outlook. Environ. Res. 2024, 247, 118268. doi:10.1016/j.envres.2024.118268. [Google Scholar]
- Mills A, O’Rourk C, Moore K. Powder semiconductor photocatalysis in aqueous solution: An overview of kinetics-based reaction mechanisms. J. Photochem. Photobiol. A Chem. 2015, 310, 66–105. doi:10.1016/j.jphotochem.2015.04.011. [Google Scholar]
- Ollis DF. Kinetic disguises in heterogeneous photocatalysis. Top. Catal. 2005, 35, 217–223. doi:10.1007/s11244-005-3827-z. [Google Scholar]
- Minero C, Vione D. A quantitative evaluation of the photocatalytic performance of TiO2 slurries. Appl. Catal. B Environ. 2006, 67, 257–269. doi:10.1016/j.apcatb.2006.05.011. [Google Scholar]
- Minero C, Bedini A, Minella M. On the standardization of the photocatalytic gas/solid test. Int. J. Chem. React. Eng. 2013, 11, 717–732. doi:10.1515/ijcre-2012-0045. [Google Scholar]
- Minero C. Kinetic analysis of photoinduced reactions at the water semiconductor interface. Catal. Today 1999, 54, 205–216. doi:10.1016/S0920-5861(99)00183-2. [Google Scholar]
- Ollis DF. Kinetics of liquid phase photocatalyzed reactions: An illuminating approach. J. Phys. Chem. B 2005, 109, 2439–2444. doi:10.1021/jp040236f. [Google Scholar]
- Pruden AL, Ollis DF. Photoassisted heterogeneous catalysis: The degradation of trichloroethylene in water. J. Catal. 1983, 82, 404–417. doi:10.1016/0021-9517(83)90207-5. [Google Scholar]
- Ollis DF. Contaminant degradation in water. Environ. Sci. Technol. 1985, 19, 480–484. doi:10.1021/es00136a002. [Google Scholar]
- Minero C, Maurino V, Vione D. Photocatalytic mechanisms and reaction pathways drawn from kinetic and probe molecules. In Photocatalysis and Water Purification: From Fundamentals to Recent Applications; Pichat P, Ed.; Wiley-VCH: Weinheim, Germany, 2013; pp. 53–72; ISBN 978-3-527-33187-1. [Google Scholar]
- Cunningham J, Srijaranai S. Isotope-effect evidence for hydroxyl radical involvement in alcohol photo-oxidation sensitized by TiO2 in aqueous suspension. J. Photochem. Photobio. A Chem. 1988, 43, 329–335. doi:10.1016/1010-6030(88)80029-7. [Google Scholar]
- Turchi CS, Ollis DF. Photocatalytic Degradation of Organic Water Contaminants: Mechanisms Involving Hydroxyl Radical Attack. J. Catalysis 1990, 122, 178–192. doi:10.1016/0021-9517(90)90269-P. [Google Scholar]
- Minero C. A rigorous kinetic approach to model primary oxidative steps of photocatalytic degradations. Sol. Energy Mater. Sol. Cells 1995, 38, 421–430. doi:10.1016/0927-0248(94)00234-7. [Google Scholar]
- Gerischer H. Photocatalysis in aqueous solution with small TiO2 particles and the dependence of the quantum yield on particle size and light intensity. Electrochim. Acta 1995, 40, 1277–1281. doi:10.1016/0013-4686(95)00058-M. [Google Scholar]
- Minero C, Catozzo F, Pelizzetti E. Role of Adsorption in Photocatalyzed Reactions of Organic Molecules in Aqueous TiO2 Suspensions. Langmuir 1992, 8, 481–486. doi:10.1021/la00038a029. [Google Scholar]
- Pellegrino F, Pellutiè L, Sordello F, Minero C, Ortel E, Hodoroaba V-D, et al. Influence of agglomeration and aggregation on the photocatalytic activity of TiO2 nanoparticles. Appl. Catal. B Environ. 2017, 216, 80–87. doi:10.1016/j.apcatb.2017.05.046. [Google Scholar]
- Calza P, Minella M, Demarchis L, Sordello F, Minero C. Photocatalytic rate dependence on light absorption properties of different TiO2 specimens. Catal. Today 2020, 340, 12–18. doi:10.1016/j.cattod.2018.10.013. [Google Scholar]
- Minero C, Pelizzetti E, Terzian R, Serpone N. Reactions of Hexafluorobenzene and Pentafluorophenol Catalyzed by Irradiated TiO2 in Aqueous Suspensions. Langmuir 1994, 10, 692–698. doi:10.1021/la00015a017. [Google Scholar]
- Theurich J, Lindner M, Bahnemann DW. Photocatalytic Degradation of 4-Chlorophenol in Aerated Aqueous Titanium Dioxide Suspensions: A Kinetic and Mechanistic Study. Langmuir 1996, 12, 6368–6376. doi:10.1021/la960228t. [Google Scholar]
- Monllor-Satoca D, Gomez R, Gonzalez-Hidalgo M, Salvador P. The “Direct–Indirect” model: An alternative kinetic approach in heterogeneous photocatalysis based on the degree of interaction of dissolved pollutant species with the semiconductor surface. Catal. Today 2007, 129, 247–255. doi:10.1016/j.cattod.2007.08.002. [Google Scholar]
- Montoya JF, Peral J, Salvador P. Comprehensive Kinetic and Mechanistic Analysis of TiO2 Photocatalytic Reactions According to the Direct–Indirect Model: (I) Theoretical Approach. J. Phys. Chem. 2014, 118, 14266–14275. doi:10.1021/jp4121645. [Google Scholar]
- Camera-Roda G, Loddo V, Palmisano L, Parrino F. Guidelines for the assessment of the rate law of slurry photocatalytic reactions. Catal. Today 2017, 281, 221–230. doi:10.1016/j.cattod.2016.06.050. [Google Scholar]
- Minella M, Minero C. Evaluation of gas/solid photocatalytic performance for the removal of VOCs at ppb and sub-ppb levels. Chemosphere 2021, 272, 129636. doi:10.1016/j.chemosphere.2021.129636. [Google Scholar]
- Minero C. Surface-Modified Photocatalysts. In Environmental Photochemistry Part III: The Handbook of Environmental Chemistry; Bahnemann DW, Robertson PKJ, Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 35, pp. 23–44. doi:10.1007/698_2013_250. [Google Scholar]
- Emeline AV, Ryabchuk VK, Serpone N. Dogmas and misconceptions in heterogeneous photocatalysis. Some enlightened reflections. J. Phys. Chem. B 2005, 109, 18515–18521. doi:10.1021/jp0523367. [Google Scholar]
- Nosaka Y. Water Photo-Oxidation over TiO2—History and Reaction Mechanism. Catalysts 2022, 12, 1557. doi:10.3390/catal12121557. [Google Scholar]
- Maurino V, Minella M, Sordello F, Minero C. A proof of the direct hole transfer in photocatalysis: The case of melamine. Appl. Catal. A Gen. 2016, 521, 57–67. doi:10.1016/j.apcata.2015.11.012. [Google Scholar]
- Minero C, Mariella G, Maurino V, Vione D, Pelizzetti E. Photocatalytic Transformation of Organic Compounds in the Presence of Inorganic Ions. 2. Competitive Reactions of Phenol and Alcohols on a Titanium Dioxide−Fluoride System. Langmuir 2000, 16, 8964–8972. doi:10.1021/la0005863. [Google Scholar]
- Minero C, Bedini A, Maurino V. Glycerol as a probe molecule to uncover oxidation mechanism in photocatalysis. Appl. Catal. B Environ. 2012, 128, 135–143. doi:10.1016/j.apcatb.2012.02.014. [Google Scholar]


