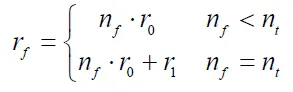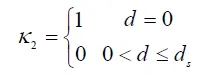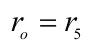1. Introduction
With the advancements of unmanned aerial vehicle (UAV) technology and materials science, the application of more affordable and compact UAVs has received significant attention. In the military sector, UAV with specialised instrumentation is able to rapidly and accurately execute missions of surveillance, search, rescue and delivery. Besides, for the non-military field, UAV shows great potential for environmental monitoring, topographic exploration, and rescue due to their flexibility [
1,
2,
3]. While on the other hand, UAV can also pose a serious threat to public safety [
4,
5]. In designated no-fly zones, such as airports and military areas, UAVs may pose an extremely serious threat to national security. In order to deal with the security threats caused by UAVs, research on civil anti-UAV systems has received widespread attention in recent decades. Typically, an anti-drone system comprises ground monitoring and jamming equipment. These systems intercept UAV targets through real-time ground detection and coordinated ground-based jamming. However, in obscured cities, communications from ground-based equipment can be severely compromised, ultimately making it difficult for anti-UAS to accurately acquire target information [
6]. In ref. [
7], a wireless sensor network is proposed by using UAVs as nodes for information acquisition and sending, the uploaded data is processed by a centralized cloud server. However, most of the researches proved that decentralized decision-making outperforms centralized ones, this paper mainly focuses on the decentralized multi-UAV systems.
UAV interception methods are mainly divided into communication jamming and capture. Most research on UAV communication jamming is focused on electromagnetic interference. Such as in ref. [
8], a UAV jamming method based on GPS signal spoofing policy is proposed. It misleads UAVs to land in the capture area by sending them fake GPS signals in real time without triggering their fault detectors. This communication jamming based interception method is extremely efficient in open environments, and superimposing jamming signals can further improve target capture rates. However, in cities where electromagnetic signals are dense and heavily obscured, interfering signals will be severely affected, and high-power interfering signals will affect the normal operation of the city. In ref. [
9], an anti-drone system that combines audio, video and radio frequency technologies is proposed to detect, localize and radio frequency jamming jam drones, which avoids the impact of high-powered equipment on cities, and the detection and jamming efficiency of targets has been greatly improved. However, this method still unavoidably relies on the support of ground-based equipment.
The interception and capture is a more straightforward method than employing communication jamming techniques. In ref. [
10], an interception method is designed based on depth image localization, which detects the target situation in an area by means of a depth image acquired by a stereo camera. Similar, ref. [
11] proposes a computer vision based stationary target localisation method which inputs the segmented processed depth images into a Deep Q-Network to acquire the UAV’s movement strategy. Note that the image technology enables UAVs to obtain more detailed and accurate information about the environment, but the window of view limitation of the on-board camera needs to be solved when intercepting targets in high-latitude continuous space.
The interception method based on image detection is able to identify and intercept the target efficiently by changing the pose and speed of the UAV. However, the time lag problem makes it difficult for UAVs to track moving targets in real time. In order to track and intercept moving targets in real time, ref. [
12] investigates an airborne interception method combined with a multi-agent system. It locates and tracks the target through on-board sensors and then interferes with the target through radio technology. Ref. [
13] proposes an anti-drone method for drone surveillance based on acoustic wave technology and infrared thermography. It locates and tracks targets in the area through detection techniques such as electromagnetic waves, acoustic waves and thermal imaging. The method improves the search efficiency of UAVs by incorporating multiple techniques. However, in a dynamically changing environment, real-time analysis and guidance for UAV searches require significant computational power, which can potentially affect the stability of the UAV’s search strategy. In order to reduce the complexity of the algorithm, a decentralized reinforcement learning search method is proposed in ref. [
14] that the effects of unknown environments is analyzed through a partially observable Markov decision process. In ref. [
15] a cooperative search method is proposed based on local information extraction. It processes the 2D grid map information within the sensor coverage by a convolutional neural network, and then the information is analyzed and guided to UAV search by an improved Q-learning. Ref. [
16] proposes a cross-domain monitoring method for tracking targets based on asymmetric self-play and curriculum learning technique. The method improves the accuracy of global information on a wide range of environments by collaboratively sensing and capturing complex environmental information by air-ground heterogeneous robots. But it still tends to convert a 3D environment into 2D space.
To the best of the authors’ knowledge, existing research on UAV interception predominantly focuses on signal-based target localization and jamming. However, there are comparatively fewer studies addressing target interception in signal-constrained regions. Especially in dynamic 3D environments with large scale, high dimensionality and more uncertainties, UAV movements need to be derived by analyzing environmental information in real time. Capturing a target as it moves through the environment also requires analyzing and learning how the target moves. Therefore, searching for and capturing a target in an unknown dynamic environment faces many challenges, which is the starting point of our work in this paper.
The main contributions of this paper are as follows: A distributed reinforcement learning target search method is proposed to enable the searching UAVs to detect all the targets while avoiding moving obstacles in a dynamically 3D environment. First, the target search problem formulation based on reinforcement learning method of an anti-UAV system is extended to continuous 3D dynamic environments. Then a reinforcement learning algorithm is proposed based on a gradient ascent method, the search decision of a S-UAV is making by optimizing the expected reward loss function. Different from the existing methods on obstacle avoidance policy, this paper divides the obstacle avoidance problem into obstacle avoidance and collision avoidance. Finally, simulations are executed to prove that the proposed method can significantly enhances the capability of UAVs in target search operations, surveillance, and exploration missions in 3D complex environments.
The paper is structured as follows. Section 2 describes the problem formulation. Section 3 proposes the distributed multi-agent search method based on policy gradient. Section 4 analyzes the experimental results of the policy gradient method. Section 5 gives the conclusions and future work.
2. Problem Formulation
In this section, the target search problem formulation based on reinforcement learning method of an anti-UAV system is described in detailed.
Supposing that there are
ns searching UAVs (S-UAV) and
nt randomly distributed targets in a 3D dynamic environment, which contains dynamic and static obstacles. The S-UAVs can sense the environment and targets through its on-board radar. The target is called detected if it is within the radar’s detection range. Assuming that the number of the targets is known, the goal of the S-UAV is to explore the environment, and ultimately find all the targets in the shortest time while avoiding obstacles. The S-UAV target search scenario in 3D dynamic environments is shown in .
. Multi-agent cooperative search system scenarios.
Without considering communication constraints, the UAV understands the environment by communicating with other UAVs in real time, and makes the best decisions based on the information. In most of the existing research, the motion of the UAV in 2D space is mainly affected by the yaw angle $$\omega_{i}$$. The velocity components of the UAV in the X-axis and Y-axis are changed by adjusting $$\omega_{i}$$. However, in 3D space, the motion of UAV in Z-axis needs to be achieved by the azimuth angle $$\phi_{i}$$. as shown in .
. Motion modeling of UAV in 2D space and 3D space.
where
Vi denotes the velocity value of the
i-th S-UAV. In addition, the angle $$\delta_{i}$$ between the S-UAV direction and the XOY plane in this paper is from
π/4 to
π/2. This is because the direction of motion of the S-UAV is synthesised by the $$\omega_{i}$$ and $$\phi_{i}$$, respectively. And when the $$\phi_i=0$$, $$\delta_i=\pi/4$$ is the maximum value. When the $$\phi_i=\pi/2$$, $$\delta_{i}=0$$ is the minimum value.
In this paper, the exploration of the
i-th S-UAV can be described by a Partially Observable Markov Decision Process (POMDP), which consists of a tuple as follows:
where $$A=(a_1,...,a_q)$$ denotes the action space with
q actions.
rt is the reward function that denotes the immediate reward obtained by the S-UAV at time step
t. $$S=\{s_0,s_1,...,s_u\}(u\leq T)$$ denotes the state space, which is shown as expressed:
where $$p_{s_i}=(x_{s_i},y_{s_i},z_{s_i})$$ denotes the
i-th S-UAV position, $$n_f(n_f\leq n_t)$$ denotes the number of target found, and $$a_i=\begin{pmatrix}\omega_i,\phi_i\end{pmatrix}$$ denotes the action selected, $$p_o=\begin{Bmatrix}p_1,p_2,...,p_{n_o}\end{Bmatrix}$$ denotes the position obstacles, which is shown as follows:
and $$O=\{o_0,o_1,...,o_u\}$$ denotes the observation space. It contains the position, yaw and azimuth of the
i-th S-UAV in 3D space, as shown in .
. Agent environment interaction.
The observations of the
i-th S-UAV are expressed as:
where $$V_{ix},V_{iy},V_{iz}$$ denote the components of velocity
Vi in the
X,
Y, and
Z-axis, respectively, they are expressed as:
In exploration, the cumulative reward consists of the immediate rewards generated by all time steps as follows:
where $$\gamma$$ is the discount factor, and
T is the maximum time step. $$J_{i,\tau}$$ denotes the return obtained by the
i-th S-UAV in each time step from reward function
rt. $$\tau$$ denotes the trajectory that contains actions, states and immediate rewards collected during iterations, which is shown as follows:
In reinforcement learning structure, the action $$a_{i}$$ is decided by the policy $$\pi_{_\theta}=p_{_\theta}(a_{_i}\mid s_{_i})$$ and exploration rate $$\varepsilon$$. $$\theta$$ denotes the weights and biases of the network. $$p_{_\theta}(a_i\mid s_i)$$ denotes the probability of S-UAV choosing action $$a_{i}$$ in state
Si, which is affected by the parameter $$\theta$$. $$\varepsilon$$ denotes the probability that the S-UAV executes action $$a_{i}$$. It decays with time steps, which suggests that the S-UAV will execute the highest probability action with 1 − $$\varepsilon$$. The decay process of $$\varepsilon$$ indicates that the S-UAV is more inclined to utilize experience as time goes by.
According to ref. [
17], when
k = 1, the S-UAV searches for targets in the environment according to an initial policy $$\pi_{\theta}$$, then generates an initial trajectory $$\tau_{1}$$. Next, the cumulative reward $$J_{i(\tau_1)}$$ is obtained and deposited into the experience pool for updating the policy $$\pi_{\theta}$$ at
k = 2. The interaction between the S-UAV and the environment is shown in .
. Agent environment interaction.
Firstly, the policy network will output the probability distribution of actions based on the state
Si of the
i-th S-UAV. Then, the actions are selected based on $$\varepsilon$$ and constitute the $$\pi_{_\theta}=p_{_\theta}(a_i\mid s_i)$$. Secondly, actions at each time step constitute $$\tau_{i}$$. Then Second, new policy network parameters are calculated based on the cumulative rewards. Finally, S-UAV will obtain a new $$\pi_{_\theta}=p_{_\theta}(a_{_i}\mid s_{_i})$$ based on the new $$\theta$$ and start a new cycle.
The goal of search problem is to maximize expected rewards as follows:
where $$p(\tau_{k}\mid\theta)$$ denotes the probability that the S-UAV selects the trajectory $$\tau_{k}$$ under policy $$\pi_{_\theta}$$. It is shown as follows:
where $$p(s_{i+1}\mid s_i,a_i)$$ is the state transfer probability of the environment, which represents the probability of transferring to state $$s_{i+1}$$ after taking action $$a_{i}$$ in state
Si.
3. Reinforcement Learning Method for Targets Search
In this section, a reinforcement learning algorithm is proposed based on a gradient ascent method, the search decision of a S-UAV is making by optimizing the expected reward loss function.
3.1. Reward Function
Reward function in a reinforcement learning target search method is a critical component that guides the behavior of the S-UAVs toward achieving their objectives. In this paper, the following reward function is designed.
3.1.1. Targeted Discovery Reward
Finding the target is the core of the search task, which is defined as follows:
where
r0 is the value for finding one target, and
r1 is the value for finding all targets. Also, $$\mathrm{r}_1>>r_0$$ makes the S-UAV search for all targets.
3.1.2. Exploration Rewards
In order to encourage a S-UAV to explore unknown regions while avoiding repetitive exploration of known regions. The search reward function is defined as:
where
np denotes the number of times explored.
3.1.3. Flying Cost
The cost of obstacle avoidance and the cost of collisions that occur after an obstacle avoidance failure, which is defined as:
where
r2,
r3 and
r4 are the cost of movement, obstacle avoidance and collision. $$\kappa_1$$, $$\kappa_2$$ determines the occurrence of obstacle avoidance and collision, as follows:
where
d denotes the distance between the S-UAV and the obstacle,
ds denotes the detection range.
When $$\kappa_1$$ = 1, the action of
i-th S-UAV will be changed as follows:
it indicates that the
i-th S-UAV will fly in the direction opposite to
Vi. In addition, the constraint $$\mid V_i\mid\leq d_s$$ is hard to ensure S-UAV avoids the dynamic obstacles. Therefore, $$\kappa_2$$ is designed as follows:
where $$\kappa_2$$ = 1 indicates that the collision occurs.
3.1.4. Cross-Border Cost
When the S-UAV crosses the map boundary, it is reset to the position of the previous time step, defined as:
where
r5 is the value of crossing the border.
3.1.5. Search Cost
In order to avoid the S-UAV from falling into a loop, the cost of time step limit is defined as:
where
r6 is the value of searching, $$\kappa_3$$ determines whether the S-UAV exceeds the time limit as follows:
In the algorithm, the reward will affect the policy update of the S-UAV, and for ease of computation, $$r_i(i=0,1,...,6)$$ is integers. Therefore, the reward obtained by each S-UAV at time step
t is defined as follows:
where $$\delta_{i}$$ is the weighting coefficients, and $$\sum\limits_{i=1}^5\delta_i=1$$.
3.2. Policy Gradient Ascent
The goal of S-UAV is to find all targets in the shortest time and at the smallest cost, which is described as maximizing expected reward in MDP [
18].
The policy is updated following the exploration of the S-UAV. In the first iteration, the observations of S-UAV are input into the initial actor network to obtain an initial policy $$\pi_{\theta}$$. Then, the S-UAV selects a series of actions to explore the environment and generates gradients to update the actor network and eventually the policy. Generally, the policy is updated by optimizing the loss function, which is shown as follows:
For convenience of calculation, $$p(\tau_k\mid\theta)$$ in the expected reward is taken logarithmically and then multiplied with the cumulative reward to define the loss function, therefore the gradient is expressed as a differential of the expected reward as follows:
According to the gradient ascent method, in order to keep the cumulative reward $$J_{i(\tau_k)}$$ approaching the desired reward $$\operatorname{E}[J_{i(\tau_k)}]$$, the parameter $$\theta $$ is updated in the direction of maximizing the expected reward [
19] as follows:
where $$\eta$$ is a constant coefficient [
20].
Based on the new $$\theta $$, the actor network will generate a new policy $$\pi_{\theta}$$ to update $$p(\tau_k\mid\theta)$$. The detailed description is given in Algorithm 1.
4. Simulation Results
In order to verify the effectiveness of the algorithm, the cooperative search of multiple UAVs in a dynamic 3D environment is simulated by the following experimental environment: The operating system is Windows 11, the processor is AMD Ryzen 5600, the graphic processor is NVIDIA RTX 3060, the RAM capacity is 32 GB, and the programming language is Python 3.8. The specific parameters of the simulation experiments as shown in .
. Example of 3D dynamic space simulation.
where the reward
ri (
i = 2, 3, 4, 5, 6) is negative, which is because the algorithm is designed to maximize the cumulative reward
rt. During exploration, UAV will adjust the probability of selecting behaviours whose reward is negative. $$\mid V_{i}\mid $$ and
ds denote the UAV velocity value and the threshold required for its obstacle avoidance, respectively.
In addition, the initial positions of the S-UAV, obstacles and targets, and the action space of the S-UAV are shown in .
. Position information and S-UAV motion space.
In the simulation, the algorithm evaluates the average cumulative reward and the average number of targets found per 100 epochs. The cumulative reward and the number of target finds generated by the S-UAV exploring the 3D environment are shown in .
. Motion trajectories of S-UAV in 3D space at different time steps.
where a,b show the convergence of the reward curve and the target discovery curve, respectively. Since the scale of the X-axis represents the average of 100 epochs, the number of target discoveries on the way is a floating point number.
shows the trend of S-UAV in the loss curve. Since $$log[p(\tau_k\mid\theta)]<0$$, the curve actually responds to the process of change in the cumulative reward $$J_{i(\tau_k)}$$.
In order to demonstrate the target search process in a 3D dynamic environment, the algorithm visualises the process as shown in . a shows the beginning of the search, b–d indicate that the S-UAV avoids the obstacle $$p_{O_2}$$, and e indicates the end of the exploration after the S-UAVs finds all the targets.
. Trajectories of S-UAV in 3D space at different time steps.
Some existing target search methods mainly focus on the 2D plane situation, such as the method in [
14], is unable to applied in 3D environment and hence cannot compare with the proposed method in this paper due to its lower dimensional space and information. Besides, the 3D space-based obstacle avoidance policy ignores the complexity of the algorithm. In order to validate the proposed 3D spatial target search method and obstacle avoidance method, shows the exploration process of the S-UAVs when the algorithm does not construct the reward functions corresponding to obstacle avoidance and collision respectively. From the results, we can see that when the time step is 80, we have $$D(p_{S_2},p_{O_2}) < d_s$$, but the S-UAV doesn’t obtain the corresponding reward feedback, as a result, the collision occurs.
. Trajectories of 3D space without constructing an obstacle avoidance reward function.
5. Conclusions
In this paper, a target search strategy based on distributed reinforcement learning method in a dynamic 3D environment is proposed. First, a motion model that is suitable for 3D space under reinforcement learning structure is proposed, then a reward functions is designed, which considers the dynamic obstacles avoidance and the UAVs collision avoidance. Besides, the network parameters are updated by the gradient ascent method, and the optimal search policy for S-UAV is finally obtained. Finally, simulation results demonstrate that the proposed method is effective in target search under 3D dynamic environments. Note that the algorithm is difficult to converge when the space shape increases. How to search stationary targets in a large range of 3D space and how to improve the tracking efficiency of moving targets are the focus of our future work.
Acknowledgments
This paper is funded by the National Key Research and Development Program of China (2023YFB4704404); R&D Program of Beijing Municipal Education Commission(M202410009014); Project of Cultivation for Young Top-notch Talents of Beijing Municipal Institutions (BPHR2022 03032); Yuxiu Innovation Project of NCUT (Project No.2024NCUTYXCX107).
Author Contributions
Conceptualization, methodology, writing—review and editing, funding acquisition, M.Z.; investigation, methodology, writing—original draft preparation, X.W.; investigation, C.W.; supervision, project administration, supervision, J.W. All authors have read and agreed to the published version of the manuscript.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
This research received no external funding.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1.
Atif M, Ahmad R, Ahmad W, Zhao L, Rodrigues JJ. UAV-assisted wireless localization for search and rescue.
IEEE Syst. J. 2021,
15, 3261–3272.
[Google Scholar]
2.
Pan Z, Zhang C, Xia Y, Xiong H, Shao X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems.
IEEE Trans. Circuits Syst. II Express Briefs 2022,
69, 1129–1133.
[Google Scholar]
3.
Kada B, Khalid M, Shaikh MS. Distributed cooperative control of autonomous multi-agent UAV systems using smooth control.
J. Syst. Eng. Electron. 2020,
31, 1297–1307.
[Google Scholar]
4.
Mekdad Y, Aris A, Babun L, El Fergougui A, Conti M, Lazzeretti R, et al. A survey on security and privacy issues of UAVs.
Comput. Netw. 2023,
224, 109626.
[Google Scholar]
5.
Li N, Su Z, Ling H, Karatas M, Zheng Y. Optimization of air defense system deployment against reconnaissance drone swarms.
Complex Syst. Model. Simul. 2023,
3, 102–117.
[Google Scholar]
6.
Park S, Kim HT, Lee S, Joo H, Kim H. Survey on anti-drone systems: Components, designs, and challenges.
IEEE Access 2021,
9, 42635–42659.
[Google Scholar]
7.
Memos VA, Psannis KE. UAV-Based Smart Surveillance System over a Wireless Sensor Network.
IEEE Commun. Stand. Mag. 2021,
5, 68–73.
[Google Scholar]
8.
Su J, He J, Cheng P, Chen J. A stealthy GPS spoofing strategy for manipulating the trajectory of an unmanned aerial vehicle.
IFAC-Pap. 2016,
49, 291–296.
[Google Scholar]
9.
Shi X, Yang C, Xie W, Liang C, Shi Z, Chen J. Anti-drone system with multiple surveillance technologies: Architecture, implementation, and challenges.
IEEE Commun. Mag. 2018,
56, 68–74.
[Google Scholar]
10.
Vrba M, Heřt D, Saska M. Onboard marker-less detection and localization of non-cooperating drones for their safe interception by an autonomous aerial system.
IEEE Robot. Autom. Lett. 2019,
4, 3402–3409.
[Google Scholar]
11.
Souli N, Kolios P, Ellinas G. Multi-agent system for rogue drone interception.
IEEE Robot. Autom. Lett. 2023,
8, 2221–2228.
[Google Scholar]
12.
Wei XL, Huang XL, Lu T, Song GG. An Improved Method Based on Deep Reinforcement Learning for Target Searching. In Proceedings of the 2019 4th International Conference on Robotics and Automation Engineering (ICRAE), Singapore, 22–24 November 2019; pp. 130–134.
13.
Hossain MS, Yang J, Lu J, Han C, Alhamid MF. MT-AAAU: Design of Monitoring and Tracking for Anti-Abuse of Amateur UAV.
Mobile Netw. Appl. 2018,
23, 328–335.
[Google Scholar]
14.
Sun Y, Wu Z, Zhang Q, Shi Z, Zhong Y. Multi-agent reinforcement learning for distributed cooperative targets search. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; pp. 711–716.
15.
Hou Y, Zhao J, Zhang R, Cheng X, Yang L. Uav swarm cooperative target search: A multi-agent reinforcement learning approach.
IEEE Trans. Intell. Veh. 2024,
9, 568–578.
[Google Scholar]
16.
Gao Y, Chen J, Chen X, Wang C, Hu J, Deng F, et al. Asymmetric self-play-enabled intelligent heterogeneous multi-robot catching system using deep multi-agent reinforcement learning.
IEEE Trans. Robot. 2023,
39, 2603–2622.
[Google Scholar]
17.
Chen T, Zhang K, Giannakis GB, Başar T. Communication-efficient policy gradient methods for distributed reinforcement learning.
IEEE Trans. Control Netw. Syst. 2022,
9, 917–929.
[Google Scholar]
18.
Kurniawati H. Partially observable markov decision processes and robotics.
Annu. Rev.Control. Robot. Auton. Syst. 2022,
5, 253–277.
[Google Scholar]
19.
Zhang K, Koppel A, Zhu H, Basar T. Global convergence of policy gradient methods to (almost) locally optimal policies.
SIAM J. Control Optim. 2020,
58, 3586–3612.
[Google Scholar]
20.
Houthooft R, Chen Y, Isola P, Stadie B, Wolski F, Jonathan Ho O, et al. Evolved Policy Gradients. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2018; Volume 31.