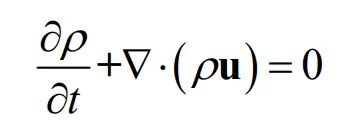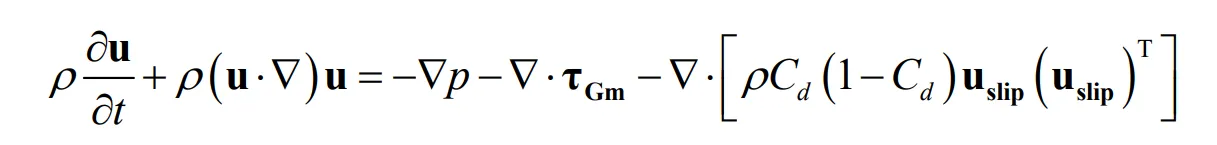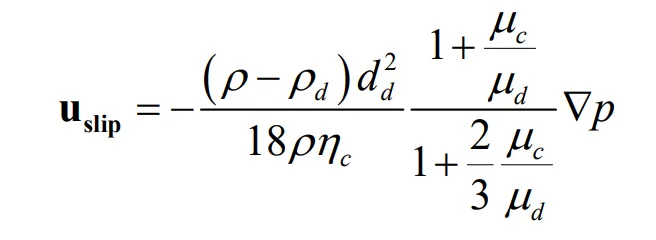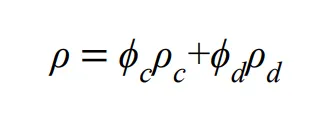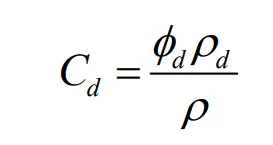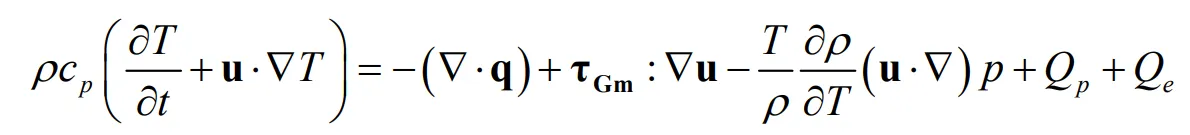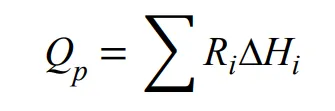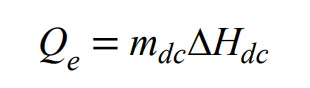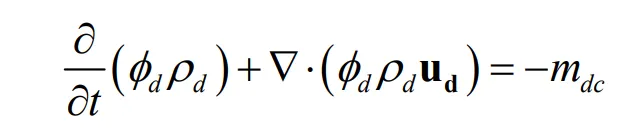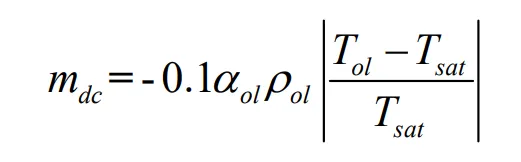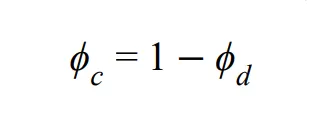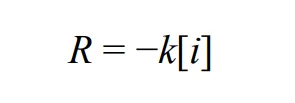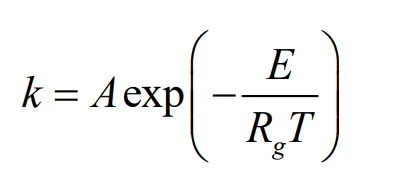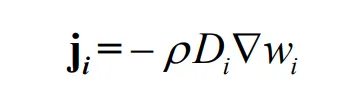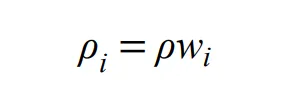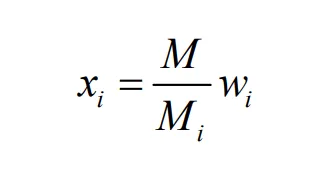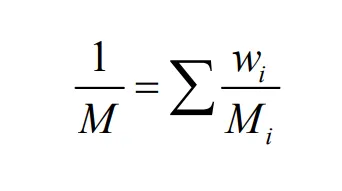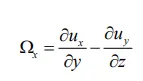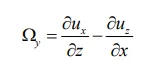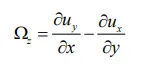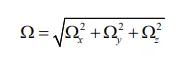Numerical Study on Pyrolysis Characteristics of Oil-Based Drilling Cuttings in a Two-Layer Screw-Driving Spiral Heat Exchanger

Zhao, Fei; Li, Yanxia; Liu, Zhongliang

doi:10.35534/ces.2024.10008

Clean Energy and Sustainability

Submit to CES

Article Open Access

Numerical Study on Pyrolysis Characteristics of Oil-Based Drilling Cuttings in a Two-Layer Screw-Driving Spiral Heat Exchanger

Fei Zhao Yanxia Li * Zhongliang Liu *

Author Information

Department of Energy Science and Engineering, Beijing University of Technology, Beijing 100124, China

Authors to whom correspondence should be addressed.

Views:228

Downloads:70

Clean Energy and Sustainability 2024, 2 (2), 10008; https://doi.org/10.35534/ces.2024.10008

Received: 10 April 2024 Accepted: 17 May 2024 Published: 23 May 2024

ABSTRACT: Oil-based drilling cuttings is a pollutive nearly-solid waste produced in oil exploitation that has to be treated for meeting clean production requirement of oil and gas exploration. A two-layer screw-driving spiral heat exchanger was thus proposed for this purpose. To investigate its effectiveness and performance, a 10-component n-decane one-step product proportional distribution chemical model was used to describe oil-based drilling cuttings pyrolysis process, and numerical simulations were carried out of forced convection inside the heat exchanger with a full consideration of pyrolysis and evaporation effects. The influences of rotation speed, screw pitch and cross-sectional shape of spiral tube on pyrolysis, flow, and heat mass transfer characteristics were studied. The results show that the heat absorbed needed for evaporation is much less than that for pyrolysis, and the heat transfer coefficient with consideration of evaporation and pyrolysis is almost two times greater than that without. The pyrolysis rate increases first, and then decreases once the temperature is higher than 838 K due to the coupled effects of temperature and reactant concentration change. The velocity, heat transfer coefficient and conversion ratio of oil-based drilling cuttings all increase with rotation speed, but the conversion ratio increase becomes slower and slower once the rotation speed exceeds 0.2 rad·s⁻¹. The average vorticity and flow resistance of oil-based drilling cuttings both decrease with screw pitch monotonously, while heat transfer coefficient increases first and then decreases because of the opposite effects of centrifugal force and thermal entrance length. Reducing screw pitch can increase conversion ratio, but once screw pitch is smaller than 800 mm, the conversion ratio approaches to a constant. Cross-sectional shape of spiral tube also affects pyrolysis performance, and circular cross-sectional spiral tube seems to be the best.

Keywords: Pyrolysis; Oil-based drilling cuttings; Numerical simulation; Heat and mass transfer

Graphical Abstract

1. Introduction

Oil-based drilling cuttings is a kind of solid waste produced in the process of oil exploitation. Due to containing a variety of toxic substances, it is not allowed to be directly discharged into environment. Usually, oil-based drilling cuttings is a complex heterogeneous mixture composed of water, heavy metal, oil, solid particles and all kinds of surfactant and various other impurities, and is in the form of a stable suspension with high viscosity, poor flow property, high degree of emulsification and complicated compositions [1,2,3]. For clean production of oil field, oil-based drilling cuttings has to be treated. Pyrolysis is one of the most promising resource recycle and harmless treatment technologies [4,5,6]. However, pyrolysis of oil-based drilling cuttings is a complex thermal chemical reaction that involves complicated chemical reaction kinetics. The relationship between pyrolysis conditions and products are very complex, and flow, heat and mass transfer, and pyrolysis in a pyrolysis device are highly coupled. Therefore, for the time being, researchers usually use thermogravimetric analysis (TGA) to study its pyrolysis characteristics by measuring the weight change of heated samples [7,8,9], so that the pyrolysis process can be analyzed from a macroscopic perspective. In open literatures, reported researches about oil-based drilling cuttings are scarce and people find that oil-based drilling cuttings has the similar components, physical and chemical properties of oil sludge. Therefore, investigations on oil sludge may give a good reference for studying the pyrolysis treatment of oil-based drilling cuttings. Prame et al. [10] studied the pyrolysis kinetic model of oil sludge generated in refinery treatment of oil-bearing wastewater at various heating rates. Their results show that the pyrolysis reaction process can be classified into two stages. In the first stage, light oil volatilizes; in the second stage, heavy oil cracks and is the main weight-loss stage of oil sludge. Schmidt et al. [11] conducted an experimental study on the pyrolysis process of oil sludge, and the results showed that temperature is the main factor affecting the pyrolysis rate. From these studies one may conclude that for oil-based drilling cuttings pyrolysis process, the main weight-loss happens in the second stage and the pyrolysis rate of oil-based drilling cuttings relies on temperature and thus the heat transfer efficiency of pyrolysis unit. Zhao et al. [12] put forward a screw-driving spiral heat exchanger using flue gas as heating fluid, combined with the flow characteristics of oil-based drilling cuttings and high heat transfer efficiency of threaded wound heat exchanger, and studied its flow and heat transfer characteristics in the screw-driving spiral heat exchanger at low temperature by numerical simulation. It was proved that the screw-driving spiral heat exchanger can not only provide higher heat transfer efficiency, but also better increase the fluidity of oil-based drilling cuttings to avoid blocking the heat exchanger flow passage. The results also showed that rotation speed, cross-sectional shape and screw pitch all have a certain influence on flow and heat transfer characteristics of oil-based drilling cuttings at low temperature, neglecting the evaporation and pyrolysis effects. It was also found in this one-layer screw-driving spiral heat exchanger that it is difficult to heat the oil-based drilling cuttings to the pyrolysis temperature. Therefore, in this paper, a two-layer screw-driving spiral heat exchanger using flue gas as heating fluid was proposed. As one may well understand, the pyrolysis and evaporation during pyrolysis process inside the screw-driving spiral heat exchanger for the treatment of oil-based drilling cuttings should have important influences on heat, mass and momentum transfer. Considering the fact that carrying out the experimental investigation of oil-based drilling cuttings pyrolysis in the screw-driving spiral heat exchanger is both complicated and expensive, and as a natural extension of our previous work [12], in this study, the influences of rotation speed, screw pitch and cross-sectional shape on flow, heat and mass transfer characteristics of oil-based drilling cuttings in our newly proposed two-layer screw-driving spiral heat exchanger with a full consideration of pyrolysis effects at high temperature are simulated numerically, so as to provide more insight understanding and reliable basic data and optimization for application of oil-based drilling cuttings pyrolysis method suggested previously [12].

2. Model Definition

2.1. Pyrolysis Mechanism Usually, preheating is carried out before pyrolysis treatment of oil-based drilling cuttings to evaporate water into steam, so as to avoid the decrease of pyrolysis rate since the water evaporation many absorb a good amount of heat and thus to ensure the quality and quantity of oil and gas recovered by pyrolysis [13,14,15,16]. Therefore, this paper will concentrate on the characteristics of oil-based drilling cuttings pyrolysis after preheating treatment (i.e., the evaporation of water in the oil-based drilling cuttings has been completed), and take oil-based drilling cuttings at the inlet of heat exchanger as a heterogeneous mixture composed of water vapor (8.94%), sediment (75.49%) and diesel (15.57%). During the pyrolysis process of oil-based drilling cuttings, the temperature will be higher than the evaporation temperature of diesel, so it will evaporate from liquid to gaseous oil. The resulted gaseous oil will further be pyrolyzed successively, which will make the flow and heat transfer phenomenon of oil-based drilling cuttings be multiple components and of complex phases. Near the evaporation or pyrolysis temperature, thermodynamic parameters and transport parameters of the mixture will change dramatically from liquid to gas or from solid to gas. Therefore, besides thermo-physical properties of oil-based drilling cuttings, the kinetic parameters and reaction mechanism during the pyrolysis process should also be given. Shie et al. [8] studied the oil sludge from a typical petroleum recycle plant. A simplified first-order reaction model was used to study pyrolysis kinetic process, and activation energy, pre-exponential factor and reaction order were respectively calculated as 7.822 × 10⁴ J·mol⁻¹, 1.58 × 10⁴ s⁻¹ and 2.92. Ma [17] studied activation energy at different stages of oil sludge composed of water (4.33%), oil (38.01%) and solid residue (54.25%) by using thermogravimetry. The results showed that the range of activation energy varies from 6.887 × 10⁴ J·mol⁻¹ to 10.383 × 10⁴ J·mol⁻¹ in the first weight-loss stage and from 4.424 × 10⁴ J·mol⁻¹ to 8.121 × 10⁴ J·mol⁻¹ in the second weight-loss stage. Wang [18] studied the oil sludge from Liaohe Oil Sewage Treatment Plant with water content of 62.31%, oil content of 29.29% and solid content of 8.40%, and it was found that the activation energy and pre-exponential factor of the first weight-loss stage were 176.42 s⁻¹ and 5.432 × 10⁴ J·mol⁻¹, and that of the second weight-loss stage were 7.75 × 107 s⁻¹ and 14.351 × 10⁴ J·mol⁻¹, respectively. The above studies show that pyrolysis kinetic parameters from different sources and components are not consistent, pyrolysis products also show different distribution characteristics with different reactants [19,20]. From the above experimental results, one can see that the generalization and application of pyrolysis kinetic parameters is very limited, and huge errors may occur if they are directly used without careful checking. As we know, diesel is a complex mixture of alkanes, naphthalene, alkenes, aromatic hydrocarbons, polycyclic aromatic hydrocarbons and other substances. As simple as it can be, the pyrolysis process of diesel oil still involves thousands of elementary reactions and enormous reactions. Therefore, it is almost impossible to accurately determine each reaction in the pyrolysis process of oil-based drilling cuttings (its constituents are much more than diesel oil). If the accurate and detailed pyrolysis mechanism model is used, the numerical simulation of oil-based drilling cuttings pyrolysis process is both time unbearable and will consume excessive computer resources. To solve this difficulty, it is necessary to simplify the reaction mechanism of the process by choosing a major hydrocarbon of diesel oil as a substitute instead of the accurate and fully-detailed pyrolysis model. n-decane is one of the major components of diesel, and it has been used as a substitute for studying pyrolysis and heat transfer performance of diesel [21,22,23,24]. Therefore, the fluid dynamics, heat and mass transfer, pyrolysis rate and pyrolysis products distribution of oil-based drilling cuttings are studied by taking it as a heterogeneous mixture consisting of n-decane, a substitute for diesel, and water vapor and sediments. Ward et al. [25] proposed a one-step product-proportional distribution chemical model (PPD) with 18 components on the basis of experimental study results on n-decane pyrolysis. This model provides a more efficient and concise reaction mechanism with high accuracy. The mechanism is as follows, C₁₀H₂₂→0.153CH₄ + 0.222C₂H₄ + 0.138C₂H₆ + 0.200C₃H₆ + 0.185C₃H₈ + 0.171C₄H₈ + 0.118C₄H₁₀ + 0.149C₅H₁₀ + 0.137C₅H₁₂ + 0.170C₆H₁₂ + 0.106C₆H₁₄ + 0.147C7H₁₄ + 0.091C₇H₁₆ + 0.132C₈H₁₆ + 0.040C₈H₁₈ + 0.046C₉H₁₈ + 0.031C₉H₂₀ Ruan et al. [26] proposed a method to simplify the overall pyrolysis reaction mechanism for n-decane, and simplified the PPD model established by Ward et al. [25]. The basic principle is as follows: during the pyrolysis of n-decane, paraffin or olefin components with large molecular mass have the same thermal physical properties, and small contribution to the heat absorbed. These large molecular mass components can therefore be considered as a whole and represented by the single component with the lowest molecular mass, that is, C₅H₁₂ is used to represent alkanes in C₅, C₆, C₇, C₈ and C₉ groups, and C₅H₁₀ is used to represent alkenes in C₅, C₆, C₇, C₈ and C₉ groups. Therefore, in the original formula, the stoichiometry of C₅H¹⁰ and C₅H₁₂ will increase, while the stoichiometry of the other substances will remain the same. In this way, the calculation time can be reduced by decreasing the number of pyrolysis reactions and mass conservation equations involved in mixture components while maintaining the calculation accuracy. The PPD mechanism with 10 components is shown as follows, C₁₀H₂₂→0.153CH₄ + 0.222C₂H₄ + 0.138C₂H₆ + 0.200C₃H₆ + 0.185C₃H₈ + 0.171C₄H₈ + 0.118C₄H₁₀ + 0.958C₅H₁₀ + 0.405C₅H₁₂ In addition, they compared chemical reaction, flow and heat transfer of n-decane in a tube with the two PPD models. The results show that the maximum relative axial velocity error was only 4.0%, and the relative conversion error was only 0.6%. Moreover, the errors of the two models on thermal property parameters are also small, say for example, the maximum relative error for density is 3.8% and for thermal conductivity 1.0%. With these acceptable small errors, the 10-component PPD model greatly reduces the number of conservation equations, the calculation time is thus reduced more than 60% compared with that of the 18-component PPD model. Therefore, the simplified pyrolysis mechanism of n-decane (the PPD model with 10 components) proposed by Ruan et al. [26] is used to describe the pyrolysis process of oil-based drilling cuttings. In addition, oil-based drilling cuttings is taken as a three-phase fluid composed of water vapor, solid sediment and diesel oil after preheating. And it is further supposed that the solid sediment does not involve mass transfer during pyrolysis process and its particle size is considered small enough to follow the flow of liquid oil and gaseous components. Therefore, the influence of sediment on flow, heat and mass transfer process of oil-based drilling cuttings is only on physical parameters of the mixture. Thus, sediment and liquid oil can be regarded as a pseudo-liquid, then oil-based drilling cuttings can be regarded as a two-phase fluid composed of dispersed phase (water vapor, gaseous oil and gas with small molecular mass generated from pyrolysis) and continuous phase (sediment and liquid oil). 2.2. Mathematical Model The mathematical model for oil-based drilling cuttings mainly includes continuity equation, momentum conservation equation, energy conservation equation and mass conservation equation. These equations can be found elsewhere such as textbooks and more directly the Handbook of COMSOL. The basic assumptions of the mathematical model are as follows: (a) The pressure fields for dispersed phase and continuous phase are same; (b) The relative velocity between the two phases is determined under the assumption that the pressure gradient and the viscous resistance are in equilibrium; (c) It is weakly compressible laminar flow for the mixture. (1) Continuity equation

(1)

(2) Momentum conservation equation The momentum conservation equation for the mixture is as follows,

(2)

where, u is velocity vector of mixture on mass average, m·s⁻¹; ρ is mixture density, kg·m⁻³; p is pressure, Pa; u_slip is slip velocity between the two phases, m·s⁻¹; τ_Gm is viscous stress, Pa; C_d is mass fraction of dispersed phase; ϕ_c and ϕ_d are volume fraction of continuous phase and dispersed phase respectively; u_c and u_d are velocity vector on mass average of continuous phase and dispersed phase, respectively, m·s⁻¹; ρ_c and ρd are density of continuous phase and dispersed phase, respectively, kg·m⁻³. Mixture velocity vector on mass average u is defined as,

(3)

Slip velocity u_slip is defined as,

(4)

where, μ_c and μ_d are dynamic viscosity of continuous phase and dispersed phase respectively, Pa·s; d_d is particle diameter of dispersed phase, and here taken as constant of 0.005 m. The mixture density is defined as,

(5)

Mass fraction of dispersed phase C_d is,

(6)

Viscous stress τ_Gm is defined as,

(7)

where, μ is mixture dynamic viscosity, Pa·s; I is unit vector. (3) Energy conservation equation The energy conservation equation for the mixture is as follows,

(8)

where, c_p is mixture heat capacity, J·kg⁻¹·K⁻¹; q is heat flux, W·m⁻³; Q_p is pyrolysis heat, i.e., the heat absorbed by pyrolysis, W·m⁻³; Q_e is evaporation heat, i.e., the heat absorbed by evaporation, W·m⁻³; Pyrolysis heat and evaporation heat are as follows respectively,

(9)

(10)

where, R_i is pyrolysis rate of component i, kg·m⁻³·s⁻¹; ∆H_i is pyrolysis reaction enthalpy of component i, J·kg⁻¹; ∆H_dc is evaporation enthalpy of component i, J·kg−¹. (4) Mass transfer process Transport equation of dispersed phase is as follows,

(11)

where, m_dc is mass transfer rate from dispersed phase to continuous phase, kg·m⁻³·s⁻¹, which is defined as follows,

(12)

where, T_sat is evaporation temperature, K; T_ol is liquid oil temperature, K; α_ol is volume fraction of liquid oil, K; ρ_ol is density of liquid oil, 616.6 kg·m⁻³. Volume fraction of continuous phase is calculated as follows,

(13)

Mass transfer taking place in pyrolysis process is shown as follows,

(14)

where, w_i is mass fraction of component i; j_i is mass flux of component i with respect to the average mass velocity, kg· m⁻²·s⁻¹; R_i is production rate or consumption rate of component i, kg·m⁻³·s⁻¹. Production rate or consumption rate R_i is calculated as,

(15)

(16)

where, [i] is concentration of component i, mol·m⁻³; k is reaction rate constant, s⁻¹; A is pre-exponential factor, 1.6 × 10¹⁵ s⁻¹; E is activation energy, 263,700 J·mol⁻¹; R_g is molar gas constant, 8.314 J·mol⁻¹·K⁻¹. Mass flux of component i is defined by average multicomponent diffusion model of the mixture,

(17)

(18)

(19)

(20)

where, D_i is mass diffusivity, m²·s⁻¹; M is average molar mass of the mixture, kg·mol⁻¹; M_i is molar mass of component i, kg·mol⁻¹; x_i is molar fraction of component i. It should be pointed out that the unsteady term is included in the above conservation equations, it is for improving numerical convergency only, that is, using unsteady form to obtain steady-state solution [27]. 2.3. Physical Model The pyrolysis temperature of n-decane is 766 K [28]. Therefore, in order to meet the pyrolysis requirements of oil-based drilling cuttings, this paper further optimizes the design of screw-driving spiral heat exchanger proposed by Zhao et al. [12]. The heating mode of one casing pipe is optimized to two casing pipes with one in upper position and one in lower position, this configuration (two-layer screw-driving spiral heat exchanger) will enhance heat transfer, increase heat exchange area and heat flux between oil-based drilling cuttings and flue gas, so as to increase the temperature of oil-based drilling cuttings. The proposed heat exchanger and the physical model is shown in Figure 1. Three identical hollow threaded pipes are wound around the screw mother tube 8 to form a casing pipe together with the shell 7, and these two identical casing pipes are fixed in the vertical upper and the lower position. Oil-based drilling cuttings flows spirally in a space formed by the wall surface of screw mother tube, spiral tube and shell. It first enters and flows out of the upper tube and then into the lower tube and from which out of the heat exchanger. Flue gas with high temperature flows in the hollow spiral tube and counter-currently with oil-based drilling cuttings both in the upper and lower tubes to increase the heat transfer temperature difference between these two fluids. It should be noted that in order to heat oil-based drilling cuttings to the required temperature, the inlet temperatures of flue gas at the upper and lower tube both are set as 1073 K and flow rate are 0.087 kg·s⁻¹. In addition, the upper and lower spiral tubes both rotate at the same speed in a direction consistent with the flow of oil-based drilling cuttings. Here, the spiral tube, screw mother tube and shell are all made of heat-resistant stainless steel 310S. Considering that the heat transfer resistance between the two fluids is much greater than that of solid metal wall, the wall thickness and the wall heat conduction thermal resistance are neglected in order to decrease computation cost. Table 1 shows the main geometrical parameters or variation ranges of two-layer screw-driving spiral heat exchanger. Figure 2 shows the diagram of grid mapping on the flow region of oil-based drilling cuttings and flue gas. Free tetrahedral mesh, which has better mesh adaptability, is used to map the flow region with complex geometrical structures on both shell side and spiral tube side. The boundary layer grid can better dispose of larger velocity gradient and temperature gradient near the wall, so as to improve the convergence of model. The boundary layer grid is set as two layers. The total number of the grid on shell side is 1103328, the average unit quality is 0.789, and the minimum unit quality is 0.374. The total number of the grid on spiral tube side is 90505, the average unit quality is 0.835, and the minimum unit quality is 0.391, which is in line with the minimum requirements for grid quality in engineering applications.

Figure 1. Physical schematic of two-layer screw-driving spiral heat exchanger. 1—flue gas inlet on the upper tube; 2—oil-based drilling cuttings inlet; 3—flue gas outlet on the upper tube; 4—flue gas outlet on the lower tube; 5—oil-based drilling cuttings outlet; 6—flue gas inlet on the lower tube; 7—shell; 8—screw mother tube; 9—spiral tube.

Figure 2. Grid mapping of two-layer screw-driving spiral heat exchanger. (a) shell side (flow region of oil-based drilling cuttings); (b) spiral tube side (flow region of flue gas).

Table 1. Main structural parameters of two-layer screw-driving spiral heat exchanger.

2.4. Numerical Simulation Method The commercial COMSOL numerical simulation software is used to solve the above physical mathematical models for flow, heat and mass transfer and pyrolysis process of oil-based drilling cuttings inside the two-layer screw-driving spiral heat exchanger. The detailed numerical models and their settings are summarized as follows. 2.4.1. The Method (1) Fluid flow process According to the above description, oil-based drilling cuttings can be taken as a two-phase fluid composed of gas and pseudo-liquid. In numerical simulation, there are two main model are most widely used, i.e., separation multiphase flow model and dispersion multiphase flow model. The separation multiphase flow model is mainly used to study small-scale problems, and it can clearly display the change of parameters in flow field such as velocity, pressure and surface tension by minutely tracing phase interface between the two phases. The dispersion multiphase flow model is mainly used to study the two-phase flow in large-scale problems. This model does not directly track the location of interface between two fluids, but track the volume fraction of each phase so as to reduce computational load. The flow of oil-based drilling cuttings in the two-layer screw-driving spiral heat exchanger belongs to large scale flow, so dispersion multiphase flow model is adopted. The calculation methods of dispersion multiphase flow model mainly include Euler-Euler model, bubble flow model and mixture model. Among them, mixture model consumes less computer resources with high accuracy in most cases. Therefore, “Mixture laminar flow model” is used to describe hydrodynamic characteristics of oil-based drilling cuttings involving mass transfer processes of evaporation and pyrolysis. The RNG k-ε turbulence model that was verified in our previous work [12] is used to describe the flow of flue gas, and omitted here for the sake of brevity. (2) Fluids heat transfer Due to large temperature difference, there exists strong heat transfer between the two fluids. Moreover, with temperature gradually increase, oil-based drilling cuttings will evaporate and pyrolyze successively. Both of these two processes are endothermic, which will affect the temperature distribution. “Fluid heat transfer model” is used to describe the heat transfer between flue gas and oil-based drilling cuttings as well as the endothermic process by evaporation and pyrolysis. (3) Mass transfer The mass transfer of oil-based drilling cuttings caused by evaporation and pyrolysis has to be taken into full consideration. For this purpose, “Transport of concentrated species model” is used to study gaseous and liquid mixtures where the species concentrations are of the same order of magnitude and none of the species can be identified as a solvent. In this case, the properties of the mixture depend on the composition, the molecular and ionic interactions between all components, and the diffusion driving forces of each component depend on the composition, temperature and pressure of mixture. Therefore, “Transport of concentrated species model” is selected to describe the mass transfer process involved in evaporation and pyrolysis of oil-based drilling cuttings. 2.4.2. Boundary Conditions The inlet temperature of oil-based drilling cuttings is set at 423 K, and its inlet mass flow rate is 0.84 kg·s⁻¹. The inlet temperature of flue gas is 1073 K, and its inlet mass flow rate is 0.087 kg·s⁻¹. Outflow conditions of flue gas and oil-based drilling cuttings are set as free flow. Moreover, all wall surfaces are regarded as non-slip wall surfaces, and the outer wall surfaces of shell and screw mother tube are set as adiabatic wall surfaces. At the inlet of oil-based drilling cuttings, mass fraction of gaseous component (water vapor) is 0.0894, and mass fraction of liquid component is 0.9106 (among which, the mass fraction of sediment and liquid oil are 0.7549 and 0.1557 respectively).

3. Grid Independence and Model Verification

3.1. Grid Independence In order to verify the numerical model introduced in the last sections is reliable, grid independence has been carried out to ensure that numerical solution for the flow, heat and mass transfer of oil-based drilling cuttings in the two-layer screw-driving spiral heat exchanger is both numerically and physically reliable and correct. The model used for grid independence test is shown in Figure 1. Under the same operation and boundary conditions, the simulation was conducted for 5 different mesh numbers. Outlet temperature and heat transfer coefficient of oil-based drilling cuttings and flue gas with the change of mesh number are shown in Table 2. It can be seen from the table that although the mesh number of grid5 (1734131) is more than doubled compared with than that of grid3 (754210), the outlet temperature and heat transfer coefficient of oil-based drilling cuttings at shell side are only change by 0.15 K and 0.02 W·m⁻²·K⁻¹, and the outlet temperature and heat transfer coefficient of flue gas in the lower tube are only changed by 0.32 K and 0.04 W·m⁻²·K⁻¹. Local parameters such temperature, velocity, and concentration were also checked and the results at typical locations are similar to that for overall parameters (outlet temperature and heat transfer coefficients). Therefore, considering the limitation of computer resources and the accuracy requirements of numerical simulation, grid4 (1193833) is adopted for calculation in this paper.

Table 2. Grid independence verification of two-layer screw-driving spiral heat exchanger.

3.2. Comparison Against Experiment Results The pyrolysis reaction of oil-based drilling cuttings is complex and it has a great influence on flow and temperature field. Therefore, it is very important to choose an appropriate reaction kinetics model for studying the pyrolysis process of oil-based drilling cuttings. As a substitute for diesel, n-decane has attracted the attention of many scholars. At present, there are many detailed pyrolysis reaction mechanisms of n-decane proposed in literatures, but most of them are not suitable for numerical simulation due to the large number of reaction components and reaction system. So, researchers proposed a one-step product-proportional distribution chemical model (PPD model), but a widely accepted PDD model still is scarce at present due to the great differences in composition and proportion of n-decane produced under different reaction conditions such as temperature and pressure. Therefore, this section our proposed model is compared against the experimental results of n-decane pyrolysis by Zhu et al. [21] and Lei et al. [28] respectively to verify the reliability of the pyrolysis reaction kinetics model. Zhu et al. [21] conducted an experimental study on the pyrolysis characteristics of n-decane in a vertical tube with a length of 940 mm. In order to keep the consistency of comparison model, the reaction conditions and reactors needs to be the same with the literature [21]. Therefore, the inlet temperature is set as 625.93 K, the inlet and outlet pressures are 4.20 MPa and 4.19 MPa, respectively. The heat transferred from outside in test section is 648.89 W, the mass flow rate is 2.19 kg·h⁻¹, the wall is insulated, and the heat flux at connecting pipe is set as 11550 W·m⁻². Lei et al. [28] investigated experimentally on the pyrolysis characteristics of n-decane in a horizontal straight tube with a circular cross section and a rectangular cross section, respectively, at a constant pressure of 3.5 MPa. Although the lengths of the circular cross-section tube and the rectangular cross-section tube are both 1560 mm, the study shows that neglecting the pre-pyrolysis stage (i.e., before passing through the inlet at 1034 mm) has no significant effect on experimental results. Therefore, only the segment from 1034 to 1560 mm, i.e., the length of the pyrolysis involved of 526 mm, is observed. In order to keep the same condition of simulation and experiment, the boundary conditions are set as follows: the inlet mass flow rate is 1.0 g·s⁻¹, heat flux at wall surface is 246 kW·m⁻², the pressure is 3.5 MPa, and the inlet temperature is 766 K. In order to keep the fluid be the fully developed flow before being heated, the inlet section is set as adiabatic. Similarly, in order to eliminate the influences of pressure outlet boundary conditions on the flow in numerical simulation, the outlet section is set as adiabatic. Figure 3(a) compared our numerical results and that of the Zhu et al. [21]. experimental investigation and numerical simulation Detailed calculations showed that the maximum error between our numerical results and the Zhu et al. [21] experimental results is 1.64%, and the maximum error between our numerical results and that of the Zhu et al. [21] numerical simulation is 2.59%. Figure 3(b) shows the comparison of our numerical simulation results with the experimental results by Lei et al. [28] on the change of n-decane conversion ratio with temperature in the horizontal straight rectangular and the circular cross-section tube, respectively. In the horizontal rectangular cross-section tube, the maximum error of n-decane conversion ratio between our numerical simulation and the Lei et al.'s experimental results [28] is 9.65%. In the horizontal circular cross-section tube, the corresponding maximum error is 11.2%. Considering the experimental uncertainty, our numerical results are both accurate and reliable and the numerical model established in previous sections can be used to study the pyrolysis characteristics of oil-based drilling cuttings.

Figure 3. Comparison between our simulation and experimental results. (a) Comparison with reference [21]; (b) Comparison with reference [28].

4. Numerical Simulation Results and Discussion

4.1. Influences of Rotation Speed The combined effects of pressure difference and relative motion to the walls of the shell and the spiral tube may prevent the oil-based drilling cuttings from clogging flow passages. Hence, the screw rotation speed should have a very strong influence on the flow, heat and mass transfer characteristics of oil-based drilling cuttings. To find out this influence, simulations are conducted for oil-based drilling cuttings flowing in a two-layers screw-driving spiral heat exchanger under 5 different screw rotation speeds, i.e., 0.001, 0.05, 0.2, 0.35, and 0.5 rad·s⁻¹ with the boundary conditions described in Section 2.4.2. 4.1.1. Flow Characteristics Figure 4(a) shows the streamlines of oil-based drilling cuttings in a two-layer screw-driving spiral heat exchanger at 0.5 rad·s⁻¹. As can be seen from the figure, the oil-based drilling cuttings flows spirally in the upper and lower tube, indicating that spiral structure can effectively change oil-based drilling cuttings flow direction and increase heat transfer area, so as to enhance heat transfer performance at shell side and improve mass transfer in evaporation and pyrolysis. Figure 4(b) shows the axial velocity of oil-based drilling cuttings at 0.5 rad·s⁻¹ and Figure 4(c) is radial velocity at the red line (i.e., z = 1000 mm, z = 2750 mm, z = 4500 mm respectively) shown in Figure 4(b). It can be seen that there is little difference in axial velocity of oil-based drilling cuttings, but a large radial velocity gradient and the maximum radial velocity at the section is offset to the outer wall, which is the result of fluid extrusion to the outer wall caused by centrifugal force. In addition, the velocity at inlet and outlet and at connecting pipe between the upper and lower tubes is significantly higher than that in main flow field of heat exchanger. This is mainly because the flow cross-sectional area of the inlet, the out and the connecting pipe is smaller than that of the passage formed by the shell tube and the screw.

Figure 4. Velocity distribution of oil-based drilling cuttings at 0.5 rad·s⁻¹. (a) Streamline diagram; (b) Velocity at x-z section; (c) Velocity at x-y section.

Figure 5 shows the average velocity of oil-based drilling cuttings at the upper and lower tube of two-layer screw-driving spiral heat exchanger at various rotation speeds. It can be found that the average velocity increases with the increase of rotation speed, and the average velocity in upper tube is slightly lower than that at lower tube, which indicates that the flow performance of oil-based drilling cuttings can be effectively improved by rotating spiral tube. Figure 6 displays the flow pressure drop of oil-based drilling cuttings at various rotation speeds. It can be seen from this figure that the flow pressure drop increases with rotation speed almost linearly, which is a simple result of the increased velocity inside the heat exchanger.

Figure 5. Average velocity in the upper and lower tube at various rotation speeds.

Figure 6. Flow pressure drop as a function of rotation speed.

4.1.2. Heat Transfer Characteristics Figure 7(a) is the axial temperature of oil-based drilling cuttings at two-layer screw-driving spiral heat exchanger, and Figure 7(b) depicts the radial temperature at the red line (i.e., z = 1000 mm, z = 2750mm, z = 4500 mm respectively) shown in Figure 7(a). It can be seen that the temperature of oil-based drilling cuttings increases gradually along the flow passage due to the heating effect of high-temperature flue gas, while the radial temperature gradient is relatively small and the highest temperature appears near the wall of the spiral tube that is in fact the heated surface.

Figure 7. Temperature distribution of oil-based drilling cuttings at 0.5 rad·s⁻¹. (a) Temperature at x-z section; (b) Temperature at x-y section.

Figure 8 shows the outlet temperature of oil-based drilling cuttings in the upper and lower tube at various rotation speeds. It can be seen from the figure that the outlet temperature in both upper and lower tube increase with the increase of rotation speed. In addition, the average outlet temperature in upper tube at 0.5 rad·s⁻¹is 713.62 K, which does not reach the required pyrolysis temperature. The design of two-layer tube can increase the heat transfer area between the two fluids, so that the oil-based drilling cuttings flowing out from the upper one can be further heated, so as to meet the pyrolysis requirements. The outlet temperature of the lower tube is 144.72~153.24 K higher than that of the upper one at five rotation speeds and well meets the pyrolysis temperature requirement.

Figure 8. Outlet temperature in the upper and lower tube as a function of rotation speed.

Figure 9 describes the relationship between the heat transfer coefficient of oil-based drilling cuttings in the upper and lower tube with rotation speed. It can be seen that as the rotation speed increases, the heat transfer coefficient in the upper and the lower both increases first quickly and then level off gradually. Although the heat transfer coefficient of oil-based drilling cuttings in the lower tube is a little bit greater than that in the upper tube, their difference gradually decreases with the increase of rotation speed. For example, the difference of heat transfer coefficient between the upper and the lower tube is 2.14 W·m⁻²·K⁻¹ at 0.001 rad·s⁻¹, and 0.75 W·m⁻²·K⁻¹ at 0.5 rad·s⁻¹. This is because the average velocity of oil-based drilling cuttings in the lower tube is slightly higher than that of the upper tube. On the other hand, the flue gas and oil-based drilling cuttings are countercurrent both in upper and lower tube, so the temperature difference between the two fluids in the upper tube is larger than that in the lower tube, and this temperature difference decreases with the increase of rotation speed. For example, when rotation speed is 0.001 rad·s⁻¹, the temperature difference between the flue gas and the oil-based drilling cuttings at the left end of upper tube (the outlet in the upper tube of oil-based drilling cuttings) is 386.29 K, while the temperature difference at the right end of lower tube (the outlet in the lower tube of oil-based drilling cuttings) is 239.14 K. And when rotation speed is 0.5 rad·s⁻¹, the temperature difference at the left end of upper tube and at the right end of lower tube is 359.38 K and 206.14 K, respectively.

Figure 9. Heat transfer coefficient in the upper and lower tube as a function of rotation speed.

4.1.3. Mass Transfer Characteristics Figure 10 depicts the volume fraction of continuous phase in the gas-liquid mixture and the mass fraction of liquid oil and gaseous oil at 0.5 rad·s⁻¹. It can be seen from this figure that the mass fraction of liquid oil at the upper tube decrease from the inlet (the liquid oil inlet mass fraction is 0.1557), and almost reduces to zero when oil-based drilling cuttings flows into the lower tube. This indicates that the evaporation of the liquid oil in the oil-based drilling cuttings mainly occurs and is finished in the upper tube. The mass fraction of gaseous oil increases along the flow at the upper tube from the inlet (0.0 at the inlet) and after that once the oil-based drilling cuttings flows into the lower tube it begins to decrease along the flow direction. This is because in the upper tube, the liquid oil evaporates into gases due to the heating effect of the flue gas and thus its mass fraction decreases and the mass fraction of the gases phase (gaseous oil) increases. However, once the oil-based drilling cuttings flows into the lower tube and is further heated, its temperature rises continuously and then the gaseous oil generated by evaporation begins to pyrolyze, this explains why the gaseous oil mass fraction decreases in the lower tube. Figure 10(c) shows the volume fraction of continuous phase in oil-based drilling cuttings. The continuous phase consists of sediment and liquid oil, in which sediment does not participate in any mass transfer process as has been discussed earlier. Therefore, the change of continuous phase volume fraction is consistent with that of liquid oil, that is, the volume fraction decreases gradually from the inlet. And in the lower tube it basically does not change along the flow direction, which again proves that the evaporation of the liquid oil phase has been completed in the upper tube. In order to describe the above phenomena took placed in the upper and lower tube of oil-based drilling cuttings more clearly, the lines of x = −335 mm and x = −1335 mm which are both 335 mm away from the center of the upper and lower tubes are used as reference. Figure 11(a) shows the evaporation rate of liquid oil along the reference line x = −335 mm at 0.5 rad·s⁻¹. As can be seen from the figure, the evaporation rate increases periodically with the temperature, and then starts to decline sharply once the temperature exceeds 670 K. This is because according to Equation (12), the evaporation rate is mainly determined by the temperature, saturation evaporation temperature and volume fraction. When the temperature exceeds saturation evaporation temperature, the liquid oil begins to evaporate, and the temperature difference is the main driving force at the beginning. Therefore, the evaporation rate increases gradually with the temperature difference, and more liquid oil evaporates resulting in the decrease of volume fraction. As the evaporation continues, the volume fraction of liquid oil begins to play a dominant role, which makes the evaporation rate decrease gradually until the liquid oil evaporates completely. Figure 11(b) shows the pyrosis rate of liquid oil along the reference line x = −1335 mm at 0.5 rad·s⁻¹ in the lower tube. It can be seen that the pyrolysis rate also increases periodically, acquires its maximum, and then begins to decline. The temperature at the turn point corresponding this variation tendency is 838 K, as indicated by the dash lines in Figure 11(b). According to Equation (16), the chemical reaction rate is related to temperature and reactant concentration. The pyrolysis rate gradually increases with the increase of temperature, which will constantly consume reactants, i.e., gaseous oil, and produce a large number of substances of small molecules. Concentration difference, on the other hand, provides the driving force for chemical reactions too. As pyrolysis reaction proceeds, the reactants are consumed, resulting in lower reactant concentration as well as the lower pyrolysis reaction rate until the reaction terminates.

Figure 10. Volume fraction of oil and liquid phase of oil-based drilling cuttings at 0.5 rad·s⁻¹. (a) Mass fraction of liquid oil; (b) Mass fraction of gaseous oil; (c) Volume fraction of continuous phase.

Figure 11. Evaporation rate and pyrolysis rate of the oil content at 0.5 rad·s⁻¹. (a) Evaporation rate in the upper tube; (b) pyrolysis rate in the lower tube.

Figure 12 shows the evaporation heat and pyrolysis heat of oil-based drilling cuttings in two-layer screw-driving spiral heat exchanger at 0.5 rad·s⁻¹. As can be seen from this figure, both evaporation and pyrolysis are endothermic processes, and the value of them both increases first and then decreases due to the evaporation and the pyrolysis rate variation tendency indicated in Figure 11. In addition, the evaporation heat is far smaller than pyrolysis heat, almost two order smaller. For example, in the case of the rotation speed of 0.5 rad·s⁻¹, the overall evaporation heat of oil-based drilling cuttings is about 23 kW, and pyrolysis heat is about 376 kW. This also indicates that the temperature difference of oil-based drilling cuttings between the upper tube and the lower tube is not only caused by the countercurrent configuration of the heat exchanger, but also by the evaporation and pyrolysis phenomena. Figure 13 shows the influences of rotation speed on mass fraction of each component of oil-based drilling cuttings in the heat exchanger. As can be seen from the figure, with the increase of rotation speed, the mass fraction of methane and other products increases gradually, while the mass fraction of gaseous oil gradually decreases. And according to the law of mass conservation and atom conservation, the mass fraction of reactants, i.e., the gaseous oil decreases more significantly than the increase of the resulted product components. In addition, the mass fraction of C₅H₁₀ produced by pyrolysis is among the largest (3.32% at 0.5 rad·s⁻¹), followed by C₅H₁₂ (1.40% at 0.5 rad·s⁻¹), and the smallest is C₄H₁₀ (0.56% at 0.5 rad·s⁻¹). The mass fraction of unsaturated hydrocarbon is higher than that of its corresponding saturated hydrocarbon for the small molecule components that is generated from gaseous oil. The pyrolysis of endothermic hydrocarbon fuels to form saturated hydrocarbons such as methane and ethane is exothermic reaction, while the pyrolysis to form unsaturated hydrocarbons such as ethylene and propylene is endothermic reaction. Therefore, oil-based drilling cuttings is more likely to generate unsaturated hydrocarbons through endothermic reaction under mild pyrolysis conditions.

Figure 12. Evaporation heat and pyrolysis heat of oil-based drilling cuttings at 0.5 rad·s⁻¹. (a) Evaporation heat; (b) Pyrolysis heat.

Figure 13. Influences of rotation speed on mass fraction of oil-based drilling cuttings at outlet.

Figure 14 displays the influences of rotation speed on the conversion ratio of oil-based drilling cuttings which is defined as the ratio of the pyrolyzed liquid oil mass fraction at the outlet of the heat exchanger to the liquid oil mass fraction at the inlet. It can be seen from the figure that the conversion ratio increases quickly with small rotation speed, and slows down once the rotation speed exceeds 0.2 rad·s⁻¹. This is because temperature increases with rotation speed, and the increased temperature can make the C-C bond broken more easily, so as to produce more free radicals and accelerate the overall chemical reaction [29]. Therefore, the higher the temperature, the higher the conversion ratio of oil-based drilling cuttings and the higher the amount of small molecule gas substances. On the other hand, referring to Figure 11, the pyrolysis reaction rate increases and then begins to decrease gradually once the temperature exceeds 838 K. As we can see at 0.2 rad·s⁻¹, the outlet temperature of oil-based drilling cuttings is 846.16 K. Therefore, although the pyrolysis reaction is still going on at this time, the reaction rate has begun to decrease, which makes the magnitude of pyrolysis rate increase gradually decreases once the rotation speed is bigger than 0.2 rad·s⁻¹.

Figure 14. Conversion ratio of oil-based drilling cuttings at different rotation speeds.

4.2. Influences of Key Structure Parameters The pyrolysis of oil-based drilling cuttings has strict requirements on temperature, so it is necessary to optimize the pyrolysis equipment to provide better heat transfer performance and ensure the stability of reaction temperature. Compared with the straight pipe, the spiral flow passage in screw-driving spiral heat exchanger has more compact structure and higher heat transfer coefficient because of the secondary flow which can be generated in the spiral channel of the heat exchanger. For practical application, the pressure drop is also important since it directly relates to the consumption of electrical and/or mechanical power, in addition to the heat transfer performance of equipment. As we know, equivalent diameter is one of the main factors affecting the pressure drop. Since the flow passage is formed by the wall of spiral tube, shell and screw mother tube in the two-layer screw-driving spiral heat exchanger, therefore screw pitch and cross-sectional shape will affect the equivalent diameter, so as to influence velocity, pressure and so on. This section will mainly study the influence of screw pitch and cross-sectional shape on flow, heat and mass transfer characteristics of oil-based drilling cuttings. 4.2.1. Screw Pitch Setting the rotation speed at 0.5 rad·s⁻¹, and maintaining the cross-sectional area and the shell length unchanged with a spiral tube of trapezoidal cross-sectional shape, the mass transfer of evaporation and pyrolysis of oil-based drilling cuttings at high temperature are investigated for the influences of screw pith on evaporation and pyrolysis, and flow and heat mass transfer characteristics of oil-based drilling cuttings. Figure 15 shows a schematic diagram of spiral tube with screw pitch of 500 mm, 700 mm, 900 mm, and 1500 mm respectively. As can be seen from the figure, the smaller the screw pitch, the longer the winding length of the spiral tube with cross-sectional shape, area and axial length unchanged. This will certainly increase the heat transfer area between flue gas and oil-based drilling cuttings and reduce the equivalent diameter of oil-based drilling cuttings flow passage.

Figure 15. Schematic diagram of spiral tube with different screw pitch.

In order to further analyze the influence of key structural parameters of spiral tube on flow characteristics of oil-based drilling cuttings, vorticity analysis is introduced. In fluid mechanics, the motion of a fluid particle with rotational angular velocity is called vortex motion, and vorticity Ω is a measurement of the rotation of a fluid particle around its own axis, which is defined by,

(21)

(22)

(23)

(24)

where, Ω_x, Ω_y, Ω_z represent the components of velocity vorticity in x, y and z direction respectively, s⁻¹; ux, uy, uz represent the components of velocity in x, y and z direction respectively, m·s⁻¹. Figure 16 presents the variation of average vorticity and overall flow pressure drop of oil-based drilling cuttings in the upper and lower tube as a function of screw pitch. As can be seen from the figure, although the average vorticity in the lower tube is slightly greater than that in the upper tube, the average vorticity in both tubes decrease with screw pitch. This is because the curvature of spiral tube and the length of flow passage of oil-based drilling cuttings both decrease with the increase of screw pitch, resulting in the decrease in centrifugal force. In addition, the pressure drop between the inlet and outlet of oil-based drilling cuttings in a two-layer screw-driving spiral heat exchanger decreases with the increase of screw pitch. The difference of flow pressure drop between screw pitch of 500 mm and screw pitch of 800 mm is 169.13 Pa, and that between 1200 mm and 1500 mm is only 22.98 Pa, which indicates that too small screw pitch will significantly increase the flow resistance of oil-based drilling cuttings. The increase of screw pitch makes the cylindrical spiral line of the screw tube extend along the axial direction, and thus straight pipes can be considered as spiral tubes with infinite pitch. Therefore, the flow resistance decreases with the increase of screw pitch. However, as one can well understand, the increase in screw pith decreases heat transfer area on one hand, and also decreases the spiral flow on the other hand, which both weaken heat transfer and reduce heat transfer coefficient of oil-based drilling cuttings.

Figure 16. Average vorticity and pressure drop at various screw pitches.

where, Ωx, Ωy, Ωz represent the components of velocity vorticity in x, y and z direction respectively, s⁻¹; ux, uy, uz represent the components of velocity in x, y and z direction respectively, m·s⁻¹. Figure 16 presents the variation of average vorticity and overall flow pressure drop of oil-based drilling cuttings in the upper and lower tube as a function of screw pitch. As can be seen from the figure, although the average vorticity in the lower tube is slightly greater than that in the upper tube, the average vorticity in both tubes decrease with screw pitch. This is because the curvature of spiral tube and the length of flow passage of oil-based drilling cuttings both decrease with the increase of screw pitch, resulting in the decrease in centrifugal force. In addition, the pressure drop between the inlet and outlet of oil-based drilling cuttings in a two-layer screw-driving spiral heat exchanger decreases with the increase of screw pitch. The difference of flow pressure drop between screw pitch of 500 mm and screw pitch of 800 mm is 169.13 Pa, and that between 1200 mm and 1500 mm is only 22.98 Pa, which indicates that too small screw pitch will significantly increase the flow resistance of oil-based drilling cuttings. The increase of screw pitch makes the cylindrical spiral line of the screw tube extend along the axial direction, and thus straight pipes can be considered as spiral tubes with infinite pitch. Therefore, the flow resistance decreases with the increase of screw pitch. However, as one can well understand, the increase in screw pith decreases heat transfer area on one hand, and also decreases the spiral flow on the other hand, which both weaken heat transfer and reduce heat transfer coefficient of oil-based drilling cuttings.

Figure 16. Average vorticity and pressure drop at various screw pitches.

Figure 17 displays the temperature distribution along the flow path in the two-layer screw-driving spiral heat exchanger with screw pitch of 700 mm, 900 mm and 1500 mm, respectively. As can be seen from this figure, the temperature of oil-based drilling cuttings in both the upper and lower tubes increase along the path and the temperature in the lower tube is higher than that in the upper tube, which is a simple result of flue gas heating. Moreover, the temperature of oil-based drilling cuttings with pitch of 700 mm is the highest among the 3 screw pitches of 700 mm, 900 mm and 1500 mm.

Figure 17. Temperature along the flow path in the upper and lower tube. (a) Temperature in the upper tube; (b) Temperature in the lower tube.

Figure 18(a) shows the density variation of oil-based drilling cuttings along the flow path in the upper tube with the screw pitches of 700 mm, 900 mm and 1500 mm. It can be seen that for all the three different screw pitch cases the density gradually decreases along the flow path in the upper tube. As it is shown, in the thermal entrance length that is from the entrance to about 2500 mm, for the upper tube, the density of oil-based drilling cuttings with 1500 mm screw pitch is the highest, followed by the screw pith of 900 mm, and 700 mm. Then, the density differences among these three screw pitches of oil-based drilling cuttings gradually decreases along the flow path. It should be noted that, although not very significantly, this tendency overturned, i.e., the greatest density is that with the smallest screw pitch and the smallest density is that with the biggest screw pitch. This is because as one of the components of oil-based drilling cuttings at inlet, the liquid oil which is of great density first reaches the evaporation temperature and evaporates into the gaseous oil that is of smaller density in the case of the largest screw pitch (1500 mm) whose temperature is the highest as shown in Figure 17(a). More gaseous oil means lower density. However, in the lower tube, the density variation follows almost completely different law. Figure 18(b) shows the density distribution of oil-based drilling cuttings along the flow path in the lower tube with the screw pitches of 700 mm, 900 mm and 1500 mm. For the case of the 1500 mm screw pitch, the density of oil-based cuttings almost remains a constant, but for the other two cases of the 700 mm and the 900 mm, although the density of oil-based drilling cuttings also shows no great change during the entrance length (about 2000 mm for the case of the 700 mm screw pitch and 3500 mm for the case of the 900 mm) and it begins to decrease dramatically along the flow path once beyond this entrance length. This means in the case of the 1500 mm screw pitch, there is no pyrolysis happens, since its outlet temperature is about 660 K which is far lower than the pyrolysis temperature of 766 K as it is stated earlier in this paper. The slight decrease in density is caused by further evaporation only in this case. However, for the other two cases, both evaporation and pyrolysis play a role in reducing density. Moreover, the density in the case of the 700 mm screw pitch shows a decline earlier and quicker than that of the case of the 900 mm screw pitch. This is because the 700 mm screw pitch case reaches the pyrolysis temperature earlier, as it is shown in Figure 17(b). Once the pyrolysis takes place, a large amount of the small molecule substances that is of small density will be generated from the gaseous oil, and this will certainly reduce the density of oil-based drilling cuttings greatly.

Figure 18. Density distribution along the flow path in the upper and lower tube. (a) Density in the upper tube; (b) Density in the lower tube.

Figure 19(a) describes the outlet temperatures of oil-based drilling cuttings in the upper and lower tubes with various screw pitches. As one can see from the figure, the outlet temperature decreases gradually with the increase of screw pitch, which is mainly a result of heat transfer area variation. Maintaining the cross-sectional shape, area and axial length of the spiral tube unchanged, the smaller screw pitch means the larger heat transfer area. Figure 19(b) presents the heat transfer coefficient of oil-based drilling cuttings in the upper and the lower tube with various screw pitches. It can be seen that the heat transfer coefficient in the upper and the lower tube both increases first and then decreases with the screw pitch. The reason for this is a little bit complicated, since the heat transfer coefficient is not only affected by the length of the flow path which mainly attributes to the thermal entrance effect for laminar flow and the flow direction. When the screw pitch is small, the flow passage is long and thus the thermal entrance effect is week. As the screw pitch increases, the flow passage length decreases, the thermal entrance effect gradually takes a dominant role and thus the heat transfer coefficient increases. On the other hand, as the screw pitch becomes bigger, the curvature diameter of flow passage is also bigger. In this case the flow inside the flow passage is more like that in a straight pipe, the non-axial velocity becomes smaller and thus the centrifugal force acting on the oil-based drilling cuttings which is an important factor that enhances convective heat transfer is weaker and weaker. Therefore, with the further increase of screw pitch, the heat transfer coefficient decreases. This explains why there exists an optimum screw pitch at which the heat transfer coefficient acquires its greatest value. Moreover, it also can be seen from the figure that this optimum screw pitch in the upper tube is smaller than that in the lower tube. This is because that the vortex of oil-based drilling cuttings in the lower tube is more vigorous than that in the upper tube as shown in Figure 16, which indicates that the fluid in the lower tube is subjected to greater centrifugal force due to the increased velocity (smaller density means greater velocity). Therefore, the heat transfer coefficient of oil-based drilling cuttings in the upper tube is more sensitive to the increase in the screw pitch.

Figure 19. Heat transfer of oil-based drilling cuttings in the upper and lower tube at different screw pitches. (a) Outlet temperature; (b) Heat transfer coefficient.

Figure 20(a) depicts the conversion ratio at the lower tube outlet as a function of screw pitch. The conversion ratio is large, and it varies a little with screw pitch, i.e., between 91.56% and 100% when screw pitch is less than 800 mm. However, once the screw pitch exceeds this value, the conversion ratio reduces rapidly. Actually, the conversion ratio is only 5.71% for the case of the 1500 mm screw pitch, which means the pyrolysis is almost neglectable. This is due to the fact that the temperature of oil-based drilling cuttings is too low for activating pyrolysis reaction and the pyrolysis rate is a function of temperature and reactant concentration. Figure 20(b) describes the change of the overall evaporation heat and the pyrolysis heat with screw pitch in the lower tube. Because the temperature of oil-based drilling cuttings is much higher than the evaporation temperature and liquid oil basically evaporates completely in the upper tube of the heat exchanger as shown in Figure 10, the evaporation heat does not change significantly with screw pitch. In addition, it can be seen that the change of pyrolysis heat is small when the screw pitch is smaller than 800 mm, and then it will decrease sharply once the screw pitch exceeds 800 mm, which is similar to the change of the conversion ratio. It can also be seen that once the pyrolysis is activated, the pyrolysis heat is significantly greater than the evaporation heat, almost an order bigger. It should be also stressed, compared with that without considering the evaporation and the pyrolysis effect, the heat transfer coefficient is more than two times greater, if one compares the heat transfer simulation results in present paper with that of our previous paper [12].

Figure 20. Influences of screw pitch on evaporation and pyrolysis of oil-based drilling cuttings. (a) Conversion ratio; (b) Evaporation heat and pyrolysis heat.

4.2.2. Cross-Sectional Shape The flow path of oil-based drilling cuttings is formed by the wall of screw mother tube, spiral tube and shell. Therefore, the equivalent diameter of flow path of oil-based drilling cuttings is different for different cross-sectional shape of the spiral tube even if the cross-sectional area is the same. Therefore, the cross-sectional shape will certainly affect flow and heat transfer characteristics. In this section, 5 different spiral tubes of different section shapes are designed, as shown in Figure 21, to study the influence of cross-sectional shape of spiral tube on flow, heat and mass transfer performance of oil-based drilling cuttings with the cross-sectional area of spiral tubes Ag (8000 mm2), shell length H and screw pitch P unchanged. Figure 22 is the diagram of the designed spiral tubes. Table 3 shows the main parameters of spiral tubes with various cross-sectional shapes.

Figure 21. Schematic diagram of five different cross-sectional shapes (sizes in mm).

Figure 22. Schematic diagram of spiral tube with different cross-sectional shapes.

Table 3. Main parameters of various spiral tube cross-sectional shapes.

Figure 23(a) describes the average vorticity of oil-based drilling cuttings in the upper and lower tube of various cross-sectional shapes. It can be seen from the figure that the average vorticity in the lower tube is higher than that in the upper tube with 5 different cross-sectional shapes. In the upper tube, the vorticity of rectangular section is the largest, followed by the arch, the square, the trapezoid, and the circular. In the lower tube, the vorticity of the arch-shaped cross-sectional spiral tube is the largest (21.933 s⁻¹), followed by the rectangle, the square, the trapezoid, and the circular. Figure 23(b) depicts the effects of cross-sectional shapes on the flow pressure drop of oil-based drilling cuttings. It can be seen that flow pressure drop of the rectangular cross-sectional spiral tube is the largest (684 Pa), followed by the arch, the trapezoidal, the square, and the circular. Among them, the pressure drop of the circular spiral tube is 51.31% smaller than that of the rectangular shaped.

Figure 23. Flow characteristics of various cross-sectional shapes. (a) Average vorticity; (b) Flow pressure drop.

Figure 24(a) depicts the influences of spiral tube cross-sectional shape on heat transfer coefficient and Nusselt number of oil-based drilling cuttings in the upper and lower tubes. As it can be seen from the figure, the heat transfer coefficient in the lower tube is greater than that in the upper tube for all cross-sectional shapes considered except for the rectangular. The differences in heat transfer coefficients between the upper and the lower tube is mainly due to the fact that the heat transfer temperature difference between oil-based drilling cuttings and flue gas and the velocity are both greater in the lower tube than lower tube, ranging from 1.08% to 3.41%. The reason for exception of the rectangular cross-sectional spiral tube is unclear, it may be quite likely due to the simulation error, since the difference of the heat transfer coefficient between the lower and the upper tube is actually small. In the upper tube, the heat transfer coefficient of the rectangular cross-sectional spiral tube is the largest, followed by the arch, the square, the trapezoid and the circular. In the lower tube, the heat transfer coefficient of the arch cross-sectional spiral tube is the largest, followed by the rectangular, square, trapezoid and circular, which is consistent with the vorticity shown in Figure 23(a), i.e., the larger the average vorticity, the greater the heat transfer coefficient. Moreover, Nusselt number, therefore, also increases with the curvature ratio described in Figure 24(a), since the curvature ratio of various cross-sectional spiral tubes as listed in the sequence from the largest to the smallest in Table 3 is the circle, the trapezoid, the square, the rectangle, and the arch. Figure 24(b) shows the effects of spiral tube cross-sectional shape on average outlet temperature of oil-based drilling cuttings in the upper and the lower tube. As we all know from Newton’s cooling law, the larger the product of heat transfer area and heat transfer coefficient, the more heat can be transferred from the high temperature flue gas to the oil-based drilling cuttings, and the average outlet temperature is determined by this product. As one can see from Table 3 that the heat transfer area of the circle is the largest, followed by the trapezoid, the square, the rectangle, and finally the arch. This explains why the average outlet temperature of the circular cross-sectional spiral tube in both the upper and lower tube is the highest, followed by the rectangle, the trapezoid, the arch, and finally the square. Figure 25 shows the influences of cross-sectional shape on conversion ratio of oil-based drilling cuttings and outlet mass fraction of gaseous oil. As can be seen from the figure, the outlet mass fraction of gaseous oil of the square cross-sectional spiral tube is the largest, followed by the arch, the rectangle, the trapezoid, and finally the circle. The conversion ratio is just opposite to that of the outlet mass fraction of gaseous oil, which can be well explained according to the pyrolysis rate equation. It should be first pointed out that the outlet conversion ratio of oil-based drilling cuttings with the five cross-sectional shapes all exceeds 90%, which proves that the designed oil-based drilling cuttings pyrolysis treatment equipment (the heat exchanger) has excellent performance. As far as the influences of the cross-sectional shape of spiral tube concerned, the outlet conversion ratio of the circular shape is the largest (99.04%) and that of the square is the smallest (91.23%). Moreover, because the pyrolysis rate increases first (<838 K) and then decreases with temperature (>838 K) as shown in Figure 11, the outlet conversion ratio of the circle, the rectangle and the trapezoid are almost the same, varies between 0.19%~0.38% only, while that between the square and the arch is a little bit bigger, 5.12%.

Figure 24. Heat transfer characteristics of various cross-sectional shapes. (a) Heat transfer coefficient and Nusselt number; (b) Outlet temperature.

Figure 25. Pyrolysis performance of various cross-sectional shapes.

5. Conclusions

In this paper, a two-layer screw-driving spiral heat exchanger is proposed for pyrolysis treatment of oil-based drilling cuttings to increase the compactness. To investigate its effectiveness, a 10-component n-decane one-step product proportional distribution chemical model is used to describe the pyrolysis process of oil-based drilling cuttings, and in dealing with the evaporation of the liquid oil in oil-based drilling cuttings only forced convective mass transfer is taken into consideration. The mathematical and physical model of evaporation and pyrolysis were established and validated and used to simulate flow, heat and mass transfer processes of oil-based drilling cuttings. The influence of evaporation and pyrolysis on flow and heat transfer characteristics is further explored. The main conclusions are as follows. (1) The proposed two-layer screw-driving spiral heat exchanger can meet the pyrolysis requirements of oil-based drilling cuttings, the greatest conversion ratio obtained is nearly 100% (99.04%). It is found that in treatment process of oil-based drilling cuttings, evaporation and pyrolysis both take places and are endothermic, evaporation heat (~23 kW) is much smaller than pyrolysis heat (~376 kW). The pyrolysis is mainly activated in the lower tube and the pyrolysis rate increases first, and then decreases along the flow path. The temperature of the turn point corresponding this variation tendency is 838 K. The evaporation mainly takes place in the upper tube of the heat exchanger, while the pyrolysis mainly in the lower tube. In addition, gaseous oil is more likely to generate unsaturated hydrocarbons in the pyrolysis process of oil-based drilling cuttings. (2) The flow, heat transfer and pyrolysis processes of oil-based drilling cuttings are mutually coupled, and temperature is the main factor affecting the pyrolysis rate. Rotation speed has a certain influence on the flow, heat transfer and pyrolysis of oil-based drilling cuttings. The velocity, heat transfer coefficient and pyrolysis rate of oil-based drilling cuttings all increase with rotation speed. The influence on conversion ratio is not linear, and becomes weaker after the rotation speed is larger than 0.2 rad·s⁻¹. On this aspect, considering the fact that at the rotation speed of 0.5 rad·s⁻¹ the conversion ratio is already greater than 99%, higher than 0.5 rad·s⁻¹ is not recommended for reducing energy consumption. (3) The influences of screw pitch on flow and heat transfer characteristics of oil-based drilling cuttings are complex. The larger the screw pitch, the smaller the average vorticity and the smaller the flow resistance; The influences of screw pitch on heat transfer coefficient of oil-based drilling cuttings are weak but complicated: it increases firstly with the screw pitch and then decreases due to the opposite effects of centrifugal force and thermal entrance length effect. The evaporation heat does not change with the screw pitch, but the pyrolysis ratio and pyrolysis heat vary with the screw pitch significantly. For small screw pitch (<800 mm), the conversion ratio and the pyrolysis heat do not change much, which means it is not a the-smaller-the-better problem in designing the heat exchanger. For large screw pitch (>800 mm) increasing the screw pitch will decrease the conversion ratio and the pyrolysis heat sharply. Therefore, 800 mm may be taken as a critical design value. (4) The influences of cross-sectional shape produced are mainly from the fact that the change in cross-sectional shape results in the corresponding variation in the equivalent diameter and curvature ratio of flow passage of oil-based drilling cuttings, which certainly will affect the flow and heat transfer characteristics. The outlet conversion ratio of the five cross-sectional shapes all are greater than 90%, and the outlet conversion ratio of the circular section is the largest and that of square section is the smallest. Considering the fact that the circular cross-sectional spiral tube is also of the smallest pressure drop and its easiness in manufacture, the circular cross-sectional spiral tube is the best choice for engineering application.

Author Contributions

Conceptualization, Z.L. and Y.L; Methodology, Software and Validation, F.Z. and Z.L.; Formal Analysis and Investigation, F.Z. and Y.L.; Resources, Z.L. and Y.L.; Writing – Original Draft Preparation, F.Z.; Writing – Review & Editing, Z.L.; Supervision, Z.L.; Project Administration, Y.L.; Funding Acquisition, Z.L.

Ethics Statement

Not applicable for studies not involving humans or animals.

Informed Consent Statement

Not applicable for studies not involving humans.

Funding

This research was funded by National Natural Science Foundation of China Project No. 52076004.

Declaration of Competing Interest

References

Wang J, Sun C, Lin BC, Huang QX, Ma ZY, Chi Y, et al. Micro- and mesoporous-enriched carbon materials prepared from a mixture of petroleum-derived oily sludge and biomass. Fuel Process. Technol. 2018, 171, 140–147. [Google Scholar]

Deng S, Wang X, Tan H, Mikulcic H, Li Z, Cao R, et al. Experimental and modeling study of the long cylindrical oily sludge drying process. Appl. Therm. Eng. 2015, 91, 354–362. [Google Scholar]

Andrew SB, Richard JS, Kirsiten S. A review of the current options for the treatment and safe disposal of drill cuttings. Waste Manag. Res. 2012, 5, 457–473. [Google Scholar]

Cheng S, Chang F, Zhang F, Huang T, Yoshikawa K, Zhang H. Progress in thermal analysis studies on the pyrolysis process of oil sludge. Thermochim. Acta 2018, 663, 125–136. [Google Scholar]

Hu G, Li J, Zeng G. Recent development in the treatment of oily sludge from petroleum industry: a review. J. Hazard. Mater. 2013, 261, 470–490. [Google Scholar]

Gao NB, Jia XY, Gao GQ, Ma ZZ, Quan C, Salman RN. Modeling and simulation of coupled pyrolysis and gasification of oily sludge in a rotary kiln. Fuel 2020, 279, 11582. [Google Scholar]

Liu J, Jiang X, Zhou L, Han X, Cui Z. Pyrolysis treatment of oil sludge and model-free kinetics analysis. J. Hazard. Mater. 2009, 161, 1208–1215. [Google Scholar]

Shie J, Chang C, Lin J, Wu C, Lee D. Resources recovery of oil sludge by pyrolysis: kinetics study. J. Chem. Technol. Biotechnol. 2000, 75, 443–450. [Google Scholar]

Chang C, Shie J, Lin J, Wu C, Lee D. Major products obtained from the pyrolysis of oil sludge. Energy Fuels 2000, 14, 1176–1183. [Google Scholar]

10.

Prame P, Vissanu M, Chatvalee K, Pramoch. Pyrolysis of API separator sludge. J. Anal. Appl. Pyrolysis 2003, 68, 547–560. [Google Scholar]

11.

Schmidt H, Kaminsky W. Pyrolysis of oil sludge in a fluidised bed reactor. Chemosphere 2001, 45, 285–290. [Google Scholar]

12.

Zhao F, Li YX, Liu ZL, Tang YZ. Flow and heat transfer characteristics of oil-based drilling cuttings in a screw-driving spiral heat exchanger. Appl. Therm. Eng. 2020, 181, 115881. [Google Scholar]

13.

Sadegh P, Kelly H. A review on condensing system for biomass pyrolysis process. Fuel Process. Technol. 2018, 180, 1–13. [Google Scholar]

14.

Noemi GL, Fonts I, Gea G, Maria BM, Luisa L. Reduction of water content in sewage sludge pyrolysis liquid by selective online condensation of the vapors. Energy Fuels 2010, 24, 6555–6564. [Google Scholar]

15.

Westerhof RJ, Brilman WFD, Garcia-Perez M, Wang Z, Kersten SRA. Fractional condensation of biomass pyrolysis vapors. Energy Fuels 2011, 25, 1817–1829. [Google Scholar]

16.

Westerhof RJ, Kuipers NJ, Kersten SR, Swaaij V, Wim P. Controlling the water content of biomass fast pyrolysis oil. Ind. Eng. Chem. Res. 2007, 46, 9238–9247. [Google Scholar]

17.

Ma ZZ. Study on Pyrolysis Characteristics of Oil Sludge in the Rotary Kiln with Solid Heat Carrier; Dalian University of Technology: Dalian, China, 2015.

18.

Wang JJ. Study on Pyrolysis Kinetics and Heat and Mass transfer Characteristics of Oily Sludge; China University of Petroleum: Beijing, China, 2013.

19.

Fonts I, Azuara M, Gea G, Murillo MB. Study of the pyrolysis liquids obtained from different sewage sludge. J. Anal. Appl. Pyrolysis 2009, 85, 184–191. [Google Scholar]

20.

Pamaudeau V, Dignac MF. The organic matter composition of various wastewater sludges and their neutral detergent fractions as revealed by pyrolysis-GC/MS. J. Anal. Appl. Pyrolysis 2007, 78, 140–152. [Google Scholar]

21.

Zhu Y, Liu B, Jiang P. Experimental and numerical investigation on n-decane thermal cracking at supercritical pressures in a vertical tube. Energy Fuels 2014, 28, 466–474. [Google Scholar]

22.

Ward TA, Ervin JS, Zabarnick S, Shafer L. Pressure effects on flowing mildly-cracked n-decane. Propuls. Power 2005, 21, 344–355. [Google Scholar]

23.

Yu J, Eser S. Thermal decomposition of C₁₀–C₁₄ normal alkanes in near-critical and supercritical regions: product distributions and reaction mechanisms. Ind. Eng. Chem. Res. 1997, 36, 574–584. [Google Scholar]

24.

Jiang J, Zhang RL, Le JL, Liu WX, Yang Y, Zhang L, et al. Regeneratively cooled scramjet heat transfer calculation and comparison with experimental data. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1227–1234. [Google Scholar]

25.

Ward TA, Ervin JS, Zabarnick S, Shafer L. Pressure effects on flowing mildly cracked n-decane. J. Propuls. Power 2005, 21, 344–355. [Google Scholar]

26.

Ruan B, Meng H, Yang V. Simplification of pyrolytic reaction mechanism and turbulent heat transfer of n-decane at supercritical pressures. Int. J. Heat Mass Transfer 2014, 69, 455–463. [Google Scholar]

27.

Tao WQ. Numerical Heat Transfer; Xi’an Jiaotong University Press: Xi’an, China, 1988.

28.

Lei Z, Liu B, Huang Q, He K, Bao Z, Zhu Q, et al. Thermal cracking characteristics of n-decane in the rectangular and circular tubes. Chin. J. Chem. Eng. 2019, 27, 2876–2883. [Google Scholar]

29.

Stewart JF. Supercritical Pyrolysis of the Endothermic Fuels Methylcyclohexane, Decalin and Tetralin; Princeton University: New Jersey, USA, 1999.

Clean Energy and Sustainability