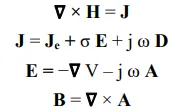1. Introduction
In today’s clean energy activities, complex procedures play a central role. Additionally, increased computing capabilities have enabled machines to perform tasks ranging, from simple automated operations, up to more sophisticated operations as, autonomous energy systems. Very often, clean energy uses electrical and electromagnetic means. Complex electromagnetic procedures use skillful control tools to monitor their behavior, which is strongly linked to the accuracy of their integrated control model.
Complexity can be encountered in addition to industrial systems, e.g., [
1,
2,
3,
4,
5,
6,
7], in various fields, e.g., neuroscience [
8] Earth climate [
9], space vehicles [
10], computer vision [
11], economics of fair division [
12], game theory of strategic interactions [
13], political science [
14] and history [
15,
16].
In general, a complex procedure is composed of a number of compound processes that interact in nonlinear interdependent spatiotemporal behaviors. Such an interaction is more complex for higher nonlinearities and closer temporal behaviors. The corresponding mathematical representation involves the coupling of process equations. Such coupling would be strong for a highly complex interaction, leading to a simultaneous solution of equations. Lower complex interactions reflect less severe and temporally distant nonlinear behavior. In this case, the coupling of the equations would be weak, characterized by an iterative solution. For linear and far temporal behaviors, the solution of the equations would be independent and the corresponding interaction is simple (not complex). The preceding discussion shows that the more complex the behaviors, the more complex the necessary models will be. In addition to taking into account functional phenomena related to compound processes, we must take into account, in the coupling of equations, other phenomena related to environmental conditions and undesirable side effects [
17]. Additionally, unintended, accidental or unforeseen events may occur in complex procedures and we must remedy their effects.
The supervision of multifunctional clean electromagnetic energy applications involving complex procedures similar to those mentioned above, must take into account the stated functional, environmental, undesirable and accidental phenomena. When monitoring simple systems, the models built into the control are often simplified to enable rapid matching between the model and the system. Thus, such a strategy would be ruled out in the presence of complexity. One of the possible solutions to deal with this complexity would be to use the real-virtual pair strategy. Such a technique can perform adaptive dynamic operation in real time, which would cut off or reduce sensing and digital uncertainties as well as accidental events. The digital twin concept employ such real-virtual pair [
18,
19,
20].
The aim of this commentary is to analyze and discuss the mathematical coupling of interactions in complex procedures and their supervision in clean electromagnetic energy systems based on a review of the literature. The novelty of this contribution lies in highlighting the assistance of mathematical coupling and model reduction in supervising the complexity in clean electromagnetic energy procedures. In the second section, the complexity and the interactions of the compound processes involved are addressed. The third section, focus on the modeling of such interactions through the mathematical coupling of the equations related to electromagnetic and other phenomena implicated in the functional and other behaviors of the systems. Compound process monitoring in complex procedures is then analyzed in section 4, taking into account threats, unsolicited external events and uncertainties related to the sensing and digital tools involved. Section 5 is focused on the discussion of additional related matters and concluded remarks of this commentary. In all sections, analyses and illustrations are supported by literature references for more information if necessary, and not for literature assessment.
2. Complexity and the Interactions of the Compound Processes
As mentioned previously, the degree of complexity is linked to the degree of non-linearity of interdependence of the interactions as well as to the degree of proximity of temporal evolution; these perform complexity spatiotemporal behavior. The degree of complexity can be classified in terms of interactions [
21]. These can be categorized corresponding to their growing complexity into three interactions natures: simple, complicated and complex. The first performs directly; complicated one behaves loosely coupled while complex interaction behaves tightly coupled. The difference between the last two is that complicated interaction does not change its conduct while the complex one is adaptive. Thus, for a given initial state, one can predict the outcome of complicated case whereas in complex one, the outcome will be subject to the interacting processes. Such complex adaptive interactions can be found in different circumstances of natural and artificial events; e.g., [
22,
23,
24,
25].
Modeling the interactions of processes involved in complex procedures implicates functional phenomena as well as other undesirable phenomena and side effects. The mathematical equations governing the behavior of these phenomena are generally solved in the harmonic or temporal domains in three-dimensional (3D) spatial geometry. Numerical analysis tools, such as finite element, are regularly used to perform studies of complex procedures and configurations where obtaining an analytical solution might not be possible. In addition, the solution is carried out locally to take into account the spatial non-linearity and the non-homogeneity of the material. This could be achieved with such discretized techniques allowing complex geometries to be considered. Space is divided into volume elements where variables are defined on nodes, edges, surfaces or volumes. Such mathematical modelling applied in the case of clean electromagnetic energy applications is the subject of the next section.
3. Modeling of Interactions in Clean Electromagnetic Case
This section is dedicated to the mathematical modeling of the interactions involved in electromagnetic applications of clean energies. This includes the different functional and associated phenomena and their behavioral coupling as well as intrinsic couplings of possible involved smart materials.
Note that for commodity and according to the nature of this contribution (short commentary), sets of equations will not be inserted in the text. These are replaced by open access references containing all of these equations.
3.1. Functional Phenomena Equations
Functional phenomena in energy activities are linked to the type of application. In the case of clean electromagnetic energy, these can be electromagnetic, electric (circuit), mechanical or thermal behavioral phenomena, in addition to the use of smart materials involving intrinsic combinations of these phenomena. The time constants in the first three phenomena are close and of a small value (rapid temporal evolution), while the thermal one is of a high value (slow temporal evolution). In this commentary, the equations governing these phenomena will not be detailed for commodity and they could be found in reference [
17].
3.1.1. Electromagnetic Equations
The equations governing the principal involved phenomenon are those of electromagnetic fields (EMFs) [
17]:
They are in terms of the electric and magnetic vector fields
E,
H and inductions
D,
B and the current density
J. The corresponding parameters, in addition to the radial frequency ω, are the magnetic permeability
B/
H= μ, the electric permittivity
D/
E = ε and the electric conductivity
J/
E = σ. The symbol
∇ is a vector of partial derivative operators and j imaginary symbol.
These equations set permit the computation, in addition to the different induced fields due to a given source, of the global quantities of the dissipated electric power loss P (see equation 4), the magnetic force F
mag (see equation 3), the magnetic flux, etc.
3.1.2. Circuit Equation
The relation of its source voltage V and its coil current i, characterize an electric circuit [
17]:
This equation is in terms of, in addition to V and i, the total resistance of the circuit r, a linear inductance L, a capacitance C, a non-linear voltage drop ᴕ (typically a semiconductor component, e.g., a diode) in the electrical circuit. The magnetic flux of the magnetic circuit is associated to a flux linkage Ψ in the coil, which induce an electromotive force (emf) in the electric circuit corresponding to its time derivative.
3.1.3. Mechanical Equations
Movement, displacement, vibration or deformation could characterize mechanical phenomena. A general form of an equation of a displacement due to external and magnetic forces can be [
17]:
This equation involves the mechanical displacement X (and its first and second time derivatives: d/dt, d
2/dt
2), the magnetic and external forces Fmag and Fext, the mass of the moving object m, the damping coefficient q, and k the spring stiffness.
3.1.4. Heat Transfer Equations
The heat transfer equation features the temperature rise due to a heat source:
This equation is in terms of the temperature rise T (and its time and space derivatives), heat source P, the thermal conductivity k, the specific heat c, and the density ρ of the substance.
3.2. Other Phenomena
In addition to functional phenomena, other events could be associated as environmental, side effects or accidental perturbations. These could be vibration, heating or exposures in general. The governing equations could be related to acoustics, fluid mechanics, biological, etc.
3.3. Coupled Phenomena Equations
The different functional (and possible other) phenomena equations could be solved in a coupled manner. The coupling may be weak (iterative) or strong (simultaneous). The concerned couplings involve behavioral and intrinsic in smart materials.
3.3.1. Behavioral Coupling
These are the couplings due to the interaction of different functional phenomena activated in the electromagnetic procedure. The EMF-circuit coupling is achieved via I, emf in (2) and J, B in (1). The EMF-mechanical coupling is activated by the magnetic force Fmag from (1) to (3). EMF-heat transfer will take place via the electrical power dissipated P from (1) to (4). Note that each of the coupled equations could affect the different parameters of the others.
3.3.2. Smart Material Coupling
The possible included smart materials in the electromagnetic procedure have intrinsic couplings. These are mainly: magnetostrictive (magnetic–mechanic), electrostrictive (electric–mechanic), shape-memory (thermic–mechanic), and thermoelectric (thermic–electric). The first concerns nonlinear behavior and close time constants and the coupling will be strong. The second behaves linear and the solution will be direct. The last two reflect distant time constants and the coupling will be weak.
4. Supervised of Complex Procedures
The monitoring of simple controlled systems use simplified models permitting fast online computations and so, a swift matching system-model. The higher precis is the model, such matching would be better but the model computing time will be higher and the speed of online matching would be lower. Thus, we need a compromise between model precision and online matching speed. Different control applications can be encountered in clean energy applications considering adaptive dynamics behaviors, predictive Control strategies and risk-constrained operations; see e.g., [
26,
27,
28,
29,
30].
4.1. Behaviors of Complexity
In the case of complex procedures, the last discussed challenge will be more significant, because the higher the procedure complexity is, higher the model complexity will be and the longer the model computation time will be. In such complexity circumstances we need, a closer model to the real complex procedure, a lower model computing time and reduced uncertainties for both sensing and digital tasks. These borders could be approached by techniques as IoT (internet of things) or CAE (computer-assisted engineering), the first is physically supported and the second is numerically maintained. These techniques perform well in identified procedures with well-known behaviors. However, it is crucial to diminish and command the irregular and unwanted behaviors that arise in these complex procedures that comprise systematically complex interactions. Attaining such an objective necessitates a paired real—model twin experienced in the relevant procedure [
19]. Such a pair diverges from both IoT and CAE by centering on both the real physical and virtual digital domains.
4.2. Real-Virtual Matching Pair
Such a pair of real-virtual allows for self-correcting behavior. The real side provides the sensing processed data to the virtual part while this latest advances control directives to the real side. Such a pairing also makes it possible to mitigate uncertainties and to alleviate all unwanted and endangering operating singularities. This matching is accompanied by processing actions. Processed information of the real side provides sensed data evaluated and reflected with external data (IoT) and the learned history. The corresponding output would be, after training, transmitted as data analytics. This processed data including indications on the reduced time appropriate model will be forwarded to the virtual simulation tool. Indeed, fast pairing requires a reliable virtual replica with low calculation time. This can be achieved by reducing the digital model while keeping the physical representation faithful. Supervision using such a pair allows adaptive control for a complex and dynamic procedure.
4.3. Digital Twin
Initially, the notion of digital twin (DT) was introduced by Grieves in 2002 [
19]. A beneficial two-way tool, between the mirrored virtual and physical real spheres, typifies DT. It is constituted of three elements, which are a paired real, a real-time digital virtual element, and a processing matching link. The real part amends its conduct in coherence with the advices conveyed by the virtual part, while the latter precisely replicates the actual condition of the first. Therefore, the DT suggests a well-designed association between the real and virtual parts [
20]. Certainly, it is a live two-way allied matching process, the real corrects the virtual error and the later improves the information of the first. Such succession of recurrences escorts to an added intelligent cooperation. As stated above, the concept of DT was first presented by M. Grieves in 2002, but analogous notions existed previously, as for example the NASA Apollo missions in 1970. After the disaster of the explosion of the oxygen reservoir of Apollo 13, the mission transformed high-consistency emulators to adjust them to the actual circumstances of the destroyed spaceship and used them to land securely. This was perhaps one of the highest factual uses of a DT, which had the principal features of Grieves one even though it was not a familiar concept in 1970.
4.4. Model Reduction
As discussed earlier, comprehensive procedure models are indispensable to endorse the features, running and physical reliability of complexity concerned in clean energy procedures. The growth in procedure complexity fashions the virtual models further sophisticated and therefore enlarges the calculation time. Model reduction strategies [
31,
32,
33] use, can advance an attenuation in such time, whilst keeping appropriate physical precision. The spirit of such strategies is to retain only, the physical exhibitions and magnitudes of importance (for a given application), in a model of elevated intricacy, allowing a humble one that can be performed more easily. A second category reducing computation time and adapted for complex models involving discretized technique as finite elements is surrogate models (or metamodels) [
34,
35,
36]. These approximately emulate the complex high-faithfulness models, using less consuming time statistical models. The choice of model reducing computation time in all strategy depends strongly on the specific requests and application objectives.
4.5. Clean Energy Applications
Complexity can be encountered in various clean energy applications such as space vehicles, airplanes, electric boats, autonomous ground vehicles, etc. These applications feature advances in mathematical modeling, dynamic exploration, intelligent supervision and diagnostics. This includes various features such as state observation, battery management organizations, autonomous steering control, driver assistance utensils, electronics, electric drive sets, connections to the electrical network, security, and health defense. Such features expose a multi-component system involving intelligent automated actions that require precise and compacted models. For example, an intelligent vehicle has augmented and cognitive perception. These are covered by a system containing radar sensors, laser scanners, cameras and actuators that enable the robotics to carry out driving tasks such as condition monitoring and autonomous navigation control. DT [
37,
38,
39,
40,
41,
42,
43,
44] can often handle supervision in such an application.
Figure 1 summarizes a real-virtual pair supervision of a complex real clean energy procedure paired to its virtual replica via a matching and processing link. This represents the different analyses and discussions involved in section 4 accounting for Sections 2 and 3.
Figure 1. Summarized illustration of a matched monitoring of a complex energy procedure with its virtual model.
5. Discussion
In the present document, the investigation of monitoring the complexity of clean energy systems applications, have pointed out the benefice of such a topic. At this stage, various questions deserve to be commented:
• It should be noted that as electromagnetic energy is considered a clean source, it is subject to compliance with usual safety standards. Otherwise, EMF exposure can disrupt electronic devices, medical tools and living tissues in general. This can be verified by electromagnetic compatibility (EMC) routines using equation (1). In the case of living tissues that exhibit biological thermal effects under EMF exposure, a particular heat transfer equation must be used; this is the bio-heat equation [
45]. Compliance with safety standards guarantees risk-free conditions.
• In Section 2, we discussed the relationship between complexity and nonlinearity of interdependence of interactions. It should be noted that in electromagnetic procedures each of the phenomena involved might behave non-linearly, e.g. the relations of B and H via the permeability μ in (1), and between V and I via the nonlinear voltage drop ᴕ in (2). Additionally, the coupling behavior could also be nonlinear, e.g. the relationship between the magnetic force Fmag and the mechanical movement X in the coupling of (1) and (2).
• Concerning the modeling of the equations governing the procedure, it can be noted that the functional phenomena considered, including intelligent materials, are those desired while the other phenomena are undesired. Regarding discretized methods like finite elements practiced in electromagnetic procedures, the coupling of equations can involve desired as well as undesirable phenomena. These methods are well suited to modeling energy conversion machines that are often involved in clean energy procedures, for example [
46,
47].
• In Section 4, we considered the notion of a strategy of reduced calculation time on the virtual side to allow rapid matching of the real—virtual couple. Certainly, even if the complete model is close to reality, it might take too long. In such a case, it is necessary to reduce this time while preserving accuracy. This will depend greatly on the nature of the procedure involved. Thus, such reduction only retains the attributes of the model, which mainly affect the procedure involved.
• A complex real procedure is adapted to its virtual mathematical model replica in a DT supervision tool involved in adaptive dynamic performance. The complex behavior of the actual procedure guides to its corresponding complex model. Such complexity could be attributed to weaknesses in computational resources, real-time simulation, or the need for many multiple simulations. This complex full model is not well suited for the adequate adaptive supervision required due to its excessive computational time. The latter could be reduced using digital assistance of different strategies; the most popular are model order reduction (MOR) and substitution or surrogate model (SM). The MOR aims to reduce the computational complexity of the virtual model, particularly used in the simulation of large-scale dynamic control procedures. This consists of reducing the dimension of the state space or the degree of freedom of the model. Thus, we obtain a reduced order model, which approximates the original full complex model. Such a strategy is often used when it is unlikely to enable numerical simulation of the full control model. A SM can be used as an approximate mathematical model of a given end result, which cannot be easily determined by measurement or calculation. This is substitution modeling, also called metamodeling, or emulation, which imitates the course of the simulation as faithfully as possible while requiring reduced calculation time. SMs are built with a bottom-up data-driven methodology and rely solely on input-output behavior and are also known as behavioral or black box modeling. Note that, in the case of a single variable, this approach will be a curve fitting.
6. Conclusions
This commentary aimed to analyze and discuss the mathematical coupling of interactions in complex procedures and their supervision in clean electromagnetic energy systems based on a review of the literature. The following concluding remarks can be summarized:
• The complexity of a real energy procedure regulates the complexity of its coupled virtual model, which sizes its behavior precisely.
• The strategy for reducing model calculation time is not universal. Saving the significant attributes of the energy procedure model is contrasting for each use and choosing a time reduction strategy depends on the specific demands and goals of the use.
• Matching exercise within a real-virtual pair allows both sides of the pair to be refined and permits to respond to their uncertainties.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
This research received no external funding.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1.
Yang S, Gao L, Zhao Y, Li X. Research on the Quantitative Evaluation of the Traffic Environment Complexity for Unmanned Vehicles in Urban Roads.
IEEE Access 2021,
9, 23139–23152.
[Google Scholar]
2.
Wang S, Li Z, He C, Liu D, Zou, G. Core components-oriented modularisation methodology for complex products. Taylor Franc. 2022, 13, doi:10.1080/09544828.2022.2143702.
3.
Yildirim U, Campean F. Functional modelling of complex multi-disciplinary systems using the enhanced sequence diagram.
Res. Eng. Des. 2020,
31, 429–448.
[Google Scholar]
4.
Tomiyama T, D’Amelio V, Urbanic J, ElMaraghy W. Complexity of Multi-Disciplinary Design.
CIRP Ann. 2007,
56, 185–188.
[Google Scholar]
5.
Fang Y, Luo B, Zhao T, He D, Jiang B, Liu Q. ST-SIGMA: Spatio-temporal semantics and interaction graph aggregation for multi-agent perception and trajectory forecasting.
CAAI Trans. Intell. Technol. 2022,
7, 744–757.
[Google Scholar]
6.
Oviedo-Trespalacios O, Haque MM, King M, Washington S. Effects of road infrastructure and traffic complexity in speed adaptation behaviour of distracted drivers.
Accid. Anal. Prev. 2017,
101, 67–77.
[Google Scholar]
7.
Zhao YN, Li ZW, Gao L, Xiong J. Road-feature-based multi-parameter road complexity calculation model of model of off-road environment. Math. Problems Eng. 2018, 1952792, doi:10.1155/2018/1952792.
8.
Monteiro J, Pedro A, Silva AJ. A Gray Code model for the encoding of grid cells in the Entorhinal Cortex.
Neural. Comput. Appl. 2022,
34, 2287–2306.
[Google Scholar]
9.
Wang F, Tian D. On deep learning-based bias correction and downscaling of multiple climate models simulations.
Clim. Dyn. 2022,
59, 3451–3468.
[Google Scholar]
10.
Pendergraft JG, Carter DR, Tseng S, Landon LB, Slack KJ, Shuffler ML. Learning from the past to advance the future: the adaptation and resilience of NASA’s Spaceflight Multiteam Systems across four eras of spaceflight.
Front. Psychol. 2019,
10, 1633.
[Google Scholar]
11.
Mittal V, Bhushan B. Accelerated computer vision inference with AI on the edge. In Proceedings of the 2020 IEEE 9th International Conference on Communication Systems and Network Technologies (CSNT), Gwalior, India, 10–12 April 2020.
12.
Amanatidis G, Aziz H, Birmpas G, Li B, Moulin H, Voudouris AA, et al. Fair Division of Indivisible Goods. Recent Progress and Open Questions.
Artif. Intell. 2023,
322, 103965.
[Google Scholar]
13.
Harris K, Anagnostides I, Farina G, Khodak M, Wu ZS, Sandholm T. Meta-learning in games. arXiv 2022, arXiv:2209.14110.
14.
Esposito G, Terlizzi A. Governing wickedness in megaprojects: Discursive and institutional perspectives.
Policy Soc. 2023,
42, 131–147.
[Google Scholar]
15.
Zonneveld KAF, Harper K, Klügel K, Chen A, Lange LGD, Versteegh GJM, et al. Climate change, society, and pandemic disease in Roman Italy between 200 BCE and 600 CE.
Sci. Adv. 2024,
10, 1033.
[Google Scholar]
16.
Harper, K. Comment l’empire romain s’est effondré. Le climat, les maladies et la chute de Rome. La Découverte, Paris, 2019.
17.
Razek A. Coupled models in electromagnetic and energy conversion systems from smart theories paradigm to that of complex events: A review.
Appl. Sci. 2022,
12, 4675.
[Google Scholar]
18.
Helbing D, Sanchez-Vaquerizo JA. Digital Twins: Potentials, Ethical Issues, and Limitations. SSRN Electron. J. 2022, arXiv:2208.04289.
19.
Grieves M, Vickers J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Trans-disciplinary Perspectives on Complex Systems; Springer: Cham, Switzerland, 2017; pp. 85–113.
20.
Tao F, Sui F, Liu A, Qi Q, Zhang M, Song B, et al. Digital twin-driven product design framework.
Int. J. Prod. Res. 2019,
57, 3935–3953.
[Google Scholar]
21.
Perrow C. Normal Accidents: Living with High Risk Technologies—Updated Edition; Princeton University Press: Princeton, NJ, USA, 2011.
22.
Tolk A. Simulation-Based Optimization: Implications of Complex Adaptive Systems and Deep Uncertainty.
Information 2022,
13, 469.
[Google Scholar]
23.
Wen J, Gabrys B, Musial K. Towards Digital Twin Oriented Modeling of Complex Networked Systems and Their Dynamics: A Comprehensive Survey. arXiv 2022, arXiv:2202.09363.
24.
Oliveira Monteiro LM, Saraiva JP, Brizola Toscan R, Stadler PF, Silva-Rocha R, Nunes da Rocha U. PredicTF: Prediction of bacterial transcription factors in complex microbial communities using deep learning.
Environ. Microb. 2022,
17, 7.
[Google Scholar]
25.
Xiao W, Yang Y, Mu X, Xie Y, Tang X, Cao D, et al. Decision-Making for Autonomous Vehicles in Random Task Scenarios at Unsignalized Intersection Using Deep Reinforcement Learning. IEEE Trans Veh. Technol. 2024, 1–14, doi:10.1109/TVT.2024.3360445.
26.
Mosconi L, Farroni F, Sakhnevych A, Timpone F, Gerbino FS. Adaptive vehicle dynamics state estimator for onboard automotive applications and performance analysis.
Veh. Syst. Dyn. 2023,
61, 3244–3268.
[Google Scholar]
27.
Yang C, Wu Z, Li X, Fars A. Risk-constrained stochastic scheduling for energy hub: Integrating renewables, demand response, and electric vehicles.
Energy 2024,
288, 129680.
[Google Scholar]
28.
Liu, Z, Yuan, Q, Nie, G, Tian Y. A Multi-Objective Model Predictive Control for Vehicle Adaptive Cruise Control System Based on a New Safe Distance Model.
Int. J. Automot. Technol. 2021,
22, 475–487.
[Google Scholar]
29.
Pyun B, Seo M, Kim S, Choi H. Development of an Autonomous Driving Controller for Articulated Bus Using Model Predictive Control Algorithm with Inner Model.
Int. J. Automot. Technol. 2022,
23, 357–366.
[Google Scholar]
30.
Song Y, Huh K. Driving and steering collision avoidance system of autonomous vehicle with model predictive control based on non-convex optimization.
Adv. Mech. Eng. 2021,
13, 410.
[Google Scholar]
31.
Tol HJ, de Visser CC, Kotsonis M. Model reduction of parabolic PDEs using multivariate splines.
Int. J. Con. 2019,
92, 175–190.
[Google Scholar]
32.
Guo Z, Yan S, Xu X, Chen Z, Ren Z. Twin-model based on model order re¬duction for rotating motors.
IEEE T. Magn. 2022,
58, 1–4.
[Google Scholar]
33.
Besselink B, Tabak U, Lutowska A, van de Wouw N, Nijmeijer H, Rixen DJ, et al. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control.
J. Sound. Vib. 2013,
332, 4403–4422.
[Google Scholar]
34.
Kudela J, Matousek R. Recent advances and applications of surrogate models for finite element method computations: A review.
Soft Comput. 2022,
26, 13709–13733.
[Google Scholar]
35.
Koziel S, Pietrenko-Dabrowska A. Fundamentals of Data-Driven Surrogate Modeling. World Sci. Publ. Europe Ltd. 2022, 1–37, doi:10.1142/9781800610750 0001.
36.
Søndergaard J. Optimization Using Surrogate Models—by the Space Mapping Technique, Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2003.
37.
Brandtstaedter H, Hübner L, Jungiewicz A, Ludwig C, Tsouchnika E, Wever U. Digital twins for large electric drive trains. In the 2018 Petroleum and Chemical Industry Conference Europe (PCIC Europe), Antwerp, Belgium, 5–7 June 2018.
38.
Glaessgen EH, Stargel DS. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. In 53rd AIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012.
39.
Phanden RK, Sharma P, Dubey A. A review on simulation in digital twin for aerospace, manufacturing and robotics.
Mater. Today Proc. 2021,
38, 174–178.
[Google Scholar]
40.
Yin H, Wang L. Application and Development Prospect of Digital Twin Technology in Aerospace.
IFAC-Papers OnLine 2020,
53, 732–737.
[Google Scholar]
41.
Toso F, Torchio R, Favato A, Carlet PG, Bolognani S, Alotto P. Digital twins as electric motor soft-sensors in the automotive industry. In Proceedings of the 2021 IEEE International Workshop on Metrology for Automotive, Metro Automotive, Bologna, Italy, 1–2 July 2021.
42.
Tshoombe BK, Dos Santos JF, Araujo RCF, Fonseca WDS. Implementation of DT-based monitoring system of induction motors. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021, pp. 161–166.
43.
Li L, Aslam S, Wileman A, Perinpanayagam S. Digital twin in erospace industry: A gentle introduction.
IEEE Access 2022,
10, 9543–9562.
[Google Scholar]
44.
Aydemir H, Zengin U, Durak U. The digital twin paradigm for aircraft review and outlook AIAA Scitech 2020 Forum, 1, Part F 2020, doi:10.2514/6.2020-0553.
45.
Razek A. Assessment of EMF Troubles of Biological and Instrumental Medical Questions and Analysis of Their Compliance with Standards.
Standards 2023,
3, 227–239.
[Google Scholar]
46.
Piriou F, Razek A. Numerical simulation of a nonconventional alternator connected to a rectifier.
IEEE Trans. Energy Convers. 1990,
5, 512–518.
[Google Scholar]
47.
Antunes OJ, Bastos JPA, Sadowski N, Razek A, Santandrea L, Bouillault F, et al. Comparison between nonconforming movement methods.
IEEE Trans. Magn. 2006,
42, 599–602.
[Google Scholar]