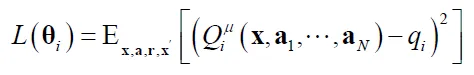Gliding aircraft are launched by rocket boosters or lifted to a certain altitude or operational area by other carriers. Then, they utilize aerodynamic principles to begin unpowered gliding outside the Earth’s atmosphere, ultimately engaging in target strikes or landing. Gliding aircraft have advantages in speed and maneuverability and possess the capability to execute long-range missions and penetrate air defense systems. Early gliding aircraft generally performed single-mission operations. However, as military technology has advanced, the traditional ‘one-on-one’ combat mode for gliding aircraft has become increasingly difficult to handle more challenging missions [
1]. The new combat mode adopts gliding aircraft clusters, engaging in point-to-point coordinated operations. Compared to the traditional ‘one-on-one’ combat mode, this method offers multiple advantages: rapid dynamic clustering based on real-time battlefield conditions, executing different tasks for different targets, providing diversity in combat strategies; the gliding aircraft can strike targets simultaneously, greatly improving strike efficiency and battlefield coverage; due to the large number and diverse routes of the cluster, it increases the difficulty of the enemy’s defense; the deterrence power of cluster attacks far exceeds that of traditional ‘one-on-one’ methods, creating greater strategic pressure on the enemy; even if some aircraft are intercepted or malfunction, other aircraft can continue the mission, ensuring the continuity and reliability of the operation. Based on these advantages, the real-time dynamic clustering and intra-cluster distributed space-time cooperative guidance architecture of gliding aircraft clusters can enhance penetration probability and achieve precise, synchronized strikes.
Gliding aircraft represent a category of vehicles, exemplified by missiles, spaceplanes, airdrop gliders, and re-entry vehicles. As shown in , they differ from traditional powered aircraft in that they are unpowered and have high cruising speeds, making timely adjustments to their flight trajectories challenging. Therefore, real-time planning of feasible trajectories for clusters of gliding aircraft becomes an essential prerequisite for coordinated control and precise landing [
2]. In the static task space, the multi-gliding aircraft cooperative problem is a typical trajectory planning problem under complex constraints [
3]. In recent years, some scholars have conducted research on trajectory planning methods for clusters or formations. Reference [
4] discusses the overall ‘resilience’ requirements of clusters and swarm-based agents such as UAVs. Reference [
5] proposed a multi-aircraft collaborative trajectory planning method based on an improved Dubins-RVO method and symplectic pseudospectral method, which can generate feasible trajectories and achieve high-precision tracking in complex environments. Reference [
6] addressed the path planning problem for multi-UAV formations in a known environment using an improved artificial potential field method combined with optimal control techniques. Reference [
7] investigated the use of an improved grey wolf optimizer algorithm to solve the multi-UAV cooperative path planning problem in complex confrontation environments. It is evident that most of these studies focus on unmanned aerial vehicles, with few dedicated to trajectory planning for gliding aircraft clusters based on their specific characteristics. Moreover, traditional trajectory planning methods often entail long computation times and pre-set trajectories that struggle to adapt to dynamic environments, leading to delayed responses and low damage efficiency in gliding aircraft clusters. Due to current onboard computing capacity limitations, trajectory optimization should be considered in an offline state [
8,
9]. Deep Reinforcement Learning offers an innovative solution for multi-objective cooperative trajectory planning for gliding aircraft clusters, enhancing aircraft clusters. coordination and combat capabilities.
Traditional deep reinforcement learning methods are mostly applied to individual learning tasks, such as value function-based reinforcement learning methods [
10,
11] and policy search-based reinforcement learning methods [
12,
13,
14,
15,
16]. There is already a considerable amount of research applying deep reinforcement learning to trajectory planning tasks for individuals. Reference [
17] addressed the three-dimensional path planning problem for UAVs in complex environments using a deep reinforcement learning approach. Reference [
18] optimized UAV trajectory and UAV-TU association using a double deep Q-network algorithm to enhance system performance and quality of service in mobile edge computing networks. Reference [
19] studied Artificial Intelligence methods and key algorithms applied to UAV swarm navigation and trajectory planning. Reference [
20] studied a method based on explainable deep neural networks to solve the problem of autonomous navigation for quadrotor UAVs in unknown environments. However, this study focuses on trajectory planning for a cluster of multiple gliding aircraft. Some scholars have already applied deep reinforcement learning methods for multi-agent collaboration to trajectory planning. Reference [
21] proposed a STAPP method based on a multi-agent deep reinforcement learning algorithm to simultaneously solve the target assignment and path planning problems for multiple UAVs in dynamic environments. Reference [
22] proposed a multi-layer path planning algorithm based on reinforcement learning, which improves UAV path planning performance in various environments by combining global and local information. Reference [
23] used a multi-agent reinforcement learning approach to solve the problem of flexible data collection path planning for UAV teams in complex environments.
Accordingly, this paper proposes a multi-objective cooperative trajectory planning method for gliding aircraft clusters based on Multi-Agent Deep Deterministic Policy Gradients (MADDPG), utilizing the three degrees of freedom of gliding aircraft, and designing a reward function with initial constraints, terminal constraints, real-time path constraints, and collision avoidance. This method can plan feasible flight trajectories in real-time for each unit in the gliding aircraft cluster, achieving coordinated multi-aircraft strikes.
3.1. Gliding Aircraft Model
This paper primarily focuses on trajectory planning during the gliding phase. Real-time responsiveness is a key consideration in the design and trajectory planning of gliding aircraft. Due to the high-speed characteristics of the aircraft, their motion states may undergo significant changes within an extremely short period. Hence, a model capable of rapid adaptation and computation is necessary to ensure the accuracy of trajectory planning. We have employed a 3-DOF model for the trajectory planning of gliding aircraft. This choice is primarily based on the high cruising speed characteristics of the gliding aircraft and the high demand for real-time computation of trajectories. Compared to more complex models with higher degrees of freedom, the 3-DOF model reduces computational load, allowing trajectory planning to be completed in a shorter time frame, thus meeting the real-time response requirements of gliding aircraft in dynamic environments. Each aircraft within the gliding aircraft cluster is established based on the following 3-DOF model:
where [
x,
y,
z] represents the position of each gliding aircraft in the cluster; [
wx,
wy,
wz] represents the wind speed components along the
x,
y, and
z axes, respectively; $$\nu_{xy}$$ denotes the horizontal velocity of each gliding aircraft; $$\nu_{z}$$ represents the vertical velocity of each gliding aircraft, which in this study is assumed to be constant as the aircraft are unpowered; $$\varphi$$ indicates the yaw angle of each gliding aircraft; $$\ddot{\varphi}$$ denotes the angular acceleration of each gliding aircraft; and
u represents the control input during flight, which in this study is set as angular acceleration.
3.2. Trajectory Constraints
The trajectory constraints of the gliding aircraft cluster determine the optimization direction of each vehicle’s trajectory planning method. Based on the mission characteristics of the gliding aircraft, the trajectory constraints should first include initial constraints and terminal constraints. The initial constraints for each individual in the gliding aircraft swarm are represented as follows:
where
t0 represents the initial time of the gliding aircraft’s mission; [
x,
y,
z] represents the initial position of the individual vehicle; and 𝜑 represents the initial yaw angle of the individual vehicle.
The terminal constraints for each gliding aircraft are as follows:
where
tf represents the terminal time; $$\left[x\left(t_f\right),y\left(t_f\right)\right]$$ represents the terminal position of the individual gliding aircraft. This paper assumes $$z_0=0$$, so the value of
tf is determined by the initial altitude
z0 and the vertical velocity
vz. Equation (3) indicates that if the vertical velocity is constant, the terminal time is also a fixed value.
In the trajectory planning model for the gliding aircraft cluster, the reward function for each aircraft needs to consider not only the terminal constraints but also real-time path constraints, control input constraints, and collision avoidance within the cluster. The reward function will be designed based on these constraints.
4.1. Reward Function
The reward function is crucial in cooperative trajectory planning for gliding aircraft clusters. Its primary purpose is to provide a quantified evaluation for the start, end, and every action step during the mission execution, guiding the gliding aircraft to make optimal decisions. The real-time reward focuses on guiding gliding aircraft towards the target point at each step and ensuring they precisely reach the target at the stipulated moment. The real-time path reward should be considered first:
where
Dt represents the horizontal distance between the system in
St state and the target point $$[x_f,y_f]$$;
d represents real-time path constraint, which is the absolute error value between the remaining flight distance of the parafoil system in the
St state and the horizontal distance from the target point.
vz is the vertical velocity of a high-speed gliding aircraft, and
vxy is the horizontal velocity.
The real-time reward value should also consider the constraints of the control input:
where
ru represents the real-time control input constraint, which needs to consider both the absolute value of the control input and its fluctuation frequency. Therefore, the real-time reward value can be described as follows:
where
K1 and
K2 are weight coefficients.
The terminal reward value focuses on the accuracy with which the aircraft reaches the predetermined target point at the end of the trajectory planning task. This paper calculates this reward based on the final distance between the aircraft and its target point. Higher rewards are given when the aircraft accurately reaches or approaches the target point:
where $$[x_{tf},y_{tf}]$$ represents the final landing position of the gliding aircraft,
Df represents the terminal error to be minimized in the trajectory planning;
K and
M are constants, with
M typically being negative. To prevent the terminal reward
rf from being diluted by the cumulative value of the real-time reward
rt,
K should be adjusted in conjunction with the value of $$\gamma$$ and tailored according to the specific task requirements.
The collision avoidance reward is designed to encourage gliding aircraft to maintain a safe distance from each other during the mission and to ensure they stay within the designated mission area. If a collision occurs between vehicles or if they go beyond the mission area, a negative reward
ra is given.
4.2. Deep Deterministic Policy Gradient
The Deep Deterministic Policy Gradient (DDPG) algorithm is a deep reinforcement learning method specifically designed for complex problems with continuous action spaces [
24]. The structure of DDPG is shown in . DDPG combines the advantages of policy-based and value-based approaches, utilizing an Actor-Critic framework. In this framework, the Actor is responsible for generating the policy by directly mapping states to actions, while the Critic evaluates the value of those actions under the given policy.
. DDPG Structure Diagram.
is the evaluated reward value after selecting control input
a in the gliding state
S:
The DDPG algorithm employs a deterministic policy $$\mu$$. Under this deterministic policy, the algorithm outputs the optimal action for a given state:
where
at is the deterministic angular acceleration value obtained directly under each state through the deterministic policy function $$\mu$$, and $$\theta^{\mu}$$ represents the parameters of the Actor Network used to generate deterministic angular acceleration.
The Actor Network $$\mu\left(S_t|\theta^\mu\right)$$ in DDPG outputs a deterministic angular acceleration, meaning that the same gliding state
S will produce the same angular acceleration
a, which can result in limited exploration samples. To increase the planning randomness and exploration of angular acceleration in the DDPG algorithm, random noise should be added to the selected angular acceleration, causing the angular acceleration value to fluctuate. The angular acceleration
a after adding noise can be expressed by the following formula:
where
N represents Gaussian noise with a normal distribution; $$\sigma$$ represents the variance;
amin is the minimum value of the angular acceleration;
amax is the maximum value of the angular acceleration.
The Actor and Critic have an estimation network and a target network, respectively. The parameters of the estimation network are trained, while the parameters of the target network are updated using a soft update method. Since the output of the target network is more stable, DDPG uses the target network to calculate the target value. The formula for the soft update of the target network is as follows:
where $$\tau$$ represents the soft update rate; $$\theta^{Q}$$ and $$\theta^{\mu}$$ are the parameters of the Actor and Critic estimation networks; $$\theta^{Q}$$ and $$\theta^{\mu}$$ are the parameters of the Actor and Critic target networks.
The actions determined by the target network of the Actor, coupled with the observed values of the environmental state, are utilized as inputs to the target network of the Critic. This process dictates the direction in which the Critic's target network parameters are updated. The formula for the parameter update within the Critic Network is as follows:
where
qi is the actual evaluation value, computed using the target network,
ri refers to the real reward received $$\gamma $$ and represents the reward decay rate. The loss function, denoted as
L, is defined as the sum of squared deviations between the actual
qi and the estimated values.
The update of the Actor Network parameters adheres to a deterministic policy:
where $$\nabla Q$$, sourced from the critic, guides the direction for updating the parameters of the actor’s network. where $$\nabla_{\theta^{\mu}}$$, sourced from the actor, guides the Actor Network to be more likely to choose the above actions.
4.3. Multi-Agent Deep Deterministic Policy Gradient
The coordinated strike strategy of gliding aircraft clusters involves forming a group of multiple aircraft to jointly attack various targets, enhancing the effectiveness of strikes and breach capabilities and increasing the likelihood of mission completion. Each aircraft in the glider cluster possesses autonomous decision-making and execution capabilities, representing a multi-agent problem where each agent has unique observations and actions.
Using traditional deep reinforcement learning methods to solve the gliding aircraft cluster task presents two challenges. The first challenge arises from the continuous update of planning strategies for each aircraft during the training process. Assuming a cluster involving
N aircraft, the environment becomes unstable from the perspective of an individual aircraft. The next state is $$S^{\prime}=P\Big(S,\mu_1\Big(\mathbf{o}_1\Big),\cdots,\mu_N\Big(\mathbf{o}_N\Big)\Big),(i=1,\cdots,N)$$, where oi represents the observation of the
i-th aircraft, and $$\mu_i\left(\mathbf{o}_i\right)$$ is the angular acceleration chosen based on this observation. Therefore, the next state is influenced by the strategies of all
N aircraft, making it infeasible to attribute environmental changes to a single planning strategy.
The second challenge is due to the differences in planning strategies among the aircraft during the collaboration process, which typically introduces high variance when using policy gradient methods. In contrast, the MADDPG algorithm is specifically designed to address the issues involved in the coordination of multiple gliding aircraft [
25]. It is based on the Actor-Critic framework of DDPG and incorporates the following improvements:
- During the training phase, each gliding aircraft can utilize the positions and observations of other aircraft.
- During the testing phase, each gliding aircraft plans its trajectory based solely on its observations.
MADDPG uses a centralized approach during the training phase and allows for distributed execution during the testing phase. Each gliding aircraft acts as an Actor and is trained with the help of a Critic. To accelerate the training process, the Critic of each aircraft utilizes other aircraft's observations and planning strategies. Each aircraft can learn the trajectory planning models of other gliding aircraft and effectively use these models to optimize its trajectory planning strategy. After the training is completed, the Actor plans trajectories based on the observations of a single aircraft, making this a distributed trajectory planning method that can be tested in a decentralized task space.
As shown in , the centralized Critic not only uses the observations of the current aircraft for training but also leverages the observation information and trajectory planning models of other aircraft. During the testing phase, the trained actor is used to distribute planning decisions. In the experience replay buffer of MADDPG, both
a and
r are vectors composed of the angular acceleration values and rewards of multiple gliding aircraft.
For the gliding aircraft cluster task, MADDPG has
N Actors and 2
N Critics.
μ = {$$\mu_1,\cdots,\mu_N$$} represents the trajectory planning strategies of
N gliding aircraft, with parameters denoted as
θ = {$$\theta_1,\ldots,\theta_N$$}. The angular acceleration of the
i-th gliding aircraft under a certain observation is given by $$\mu_i\big(a_i\big| o_i\big)$$. The policy gradient for the
i-th gliding aircraft is given by the following formula:
where
x represents the complete environmental information, that is, the observation set of the gliding aircraft cluster, denoted as $$x=\left(o_{1},\ldots,o_{N}\right)$$. In the training and testing process of the trajectory planning model, each gliding aircraft needs to obtain the observation information of other aircraft to achieve coordination and collision avoidance,
oi represents the observation information of the
i-th gliding aircraft. $$Q_i^\mu $$ is the centralized evaluation function for the i-th aircraft. Its input consists of the angular acceleration
ai chosen by each aircraft and the environmental information
x. Each
Qi is learned independently, allowing the reward for each aircraft to be designed independently. Each element in the experience replay buffer
B is a four-tuple $$\left(x_t,a_t,r_t,x_{t+1}\right)$$, recording the flight experiences of all gliding aircraft. Its structure is shown in , where $$a_t=\{a_1,\ldots,a_N\}$$ and $$r_t=\{r_1,\ldots,r_N\}$$.
The state space represents the environmental information that each glider can perceive during decision-making, typically including:
(1) The current position and velocity vector of the glider.
(2) The target location for the glider’s current mission, which guides the glider toward a predetermined destination.The relative position and velocity of nearby gliders to enable collision avoidance and coordinated planning.
Therefore, the state space can be expressed as $$o_{i_t}=(x_{i_t},y_{i_t},z_{i_t},\nu_{x_{i_t}},\nu_{z_{i_t}},x_f,y_f)$$.
The action space represents the actions each glider can choose at each decision step, which in this paper is set as the angular acceleration of the yaw angle.
. Experience replay buffer.
The centralized action-value function is updated through backpropagation:
where $$\mu^{\prime}=\left\{\mu_{\theta_i}^{\prime},\ldots,\mu_{\theta_N}^{\prime}\right\}$$ represents the action function of the target network, corresponding to the planning strategy parameters $$\theta_{i}^{\prime}$$ of the
i-th aircraft in the target network. $$\theta_{i}^{\prime}$$ is the evaluation function for the
i-th aircraft in the target network.
The pseudocode of MADDPG is shown in Algorithm 1.
4.4. Experimental Setup and Algorithm Parameters
To verify the correctness of the algorithm proposed in this study, PyCharm was used as the development and simulation environment in Python language version 3.9. shows the parameters of the MADDPG algorithm, and shows the configuration of the experimental machine.
. MADDPG algorithm parameters.
. Experimental machine configuration.
Traditional trajectory planning methods often rely on complex computational models, which substantially increase computation time in large-scale scenarios and make adaptation to dynamic environmental changes challenging. This is especially challenging when dealing with gliding aircraft clusters, where obtaining effective planning results within a short time becomes difficult. This paper proposes a multi-objective trajectory planning method for gliding aircraft clusters based on the MADDPG algorithm to address this issue. Each gliding aircraft executes trajectory planning strategies in a distributed manner based on a pre-trained model, eliminating the need to recalculate trajectories for different initial positions. Additionally, a reward function tailored to multi-objective tasks is designed for each aircraft in the cluster, considering trajectory accuracy, energy minimization, and collision avoidance within the cluster. Simulation results show that the proposed trajectory planning method can plan optimal trajectories for gliding aircraft at different positions in real-time.
To reduce the training time of the trajectory planning model and ensure real-time decision efficiency, this paper simplifies the gliding aircraft model to a 3DOF model and pre-assigns a target to each aircraft. Future research could first consider using a higher degree of freedom model while maximizing decision efficiency. Additionally, it could incorporate real-time target allocation based on the positions of different aircraft within the flight mission to improve landing accuracy and mission success rate.
This work was supported by the National Natural Science Foundation of China (Grant No.62103204).
Conceptualization, Q.S.; Methodology, H.S.; Validation, J.Y.; Writing—Original Draft Preparation, J.Y.; Writing—Review & Editing, J.Y.
Not applicable.
Not applicable.
This research received no external funding.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.