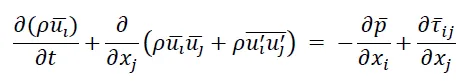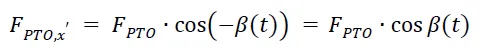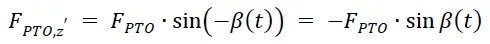1. Introduction
Harnessing the power from the ocean, wave energy converters (WECs) have an important role to play in energy generation. Due to a rapid changing climate, the quest for sustainable and clean energy sources is crucial. In the academic and industrial fields of WECs, numerous methodologies have been suggested for harnessing wave energy, and considerable endeavours are underway to reach its commercialisation.
Efforts to enhance the efficiency of Wave Energy Converters (WECs) have been made by numerous researchers, and one approach involves integrating WECs with other marine structures. According to Mustapa et al. [
1], coupling WECs with coastal structures can yield notable advantages. Firstly, it can lead to cost savings in construction, installation, and maintenance. Secondly, this integration allows for the establishment of energy production facilities while simultaneously providing infrastructure for coastal protection.
According to Zhao et al. [
2], various studies on the combination of hybrid floating breakwaters and Wave Energy Converters (WECs) were examined. The primary objective of these studies was to enhance synergy by combining the wave-damping effects achievable from floating breakwaters with the energy production obtained from WECs. Strategies for increasing the efficiency of WECs through the integration of breakwaters included altering the natural frequency of WECs using Power Take-Off (PTO) mechanisms and using stationary effect induced by reflection waves of incident waves from breakwater. Several papers have reported the phenomenon of increased motion in WECs due to stationary waves. According to the findings of some studies based on the linear potential flow theory [
3], an increase in WEC motion was observed at specific periods, and substantial performance improvements were achieved when optimal PTO damping was applied. Coiro et al. [
4] discussed the establishment of a stationary wave effect in front of a breakwater wall, resulting from the interaction between the incident wave and the wave reflected from the wall. They anticipated that this stationary wave system would be highly sensitive to the incident wavelength, influencing the power output performance. In a related study, Reabroy et al. [
5] examined the impact of the distance between the Wave Energy Converter (WEC) and the breakwater wall within a specific wave period. Their findings indicated that the breakwater effect, especially in the case of a point absorber-type WEC, could enhance the hydrodynamic performance, particularly the heave motion of the WEC. However, it is worth noting that the distance range explored in their study to determine the optimal distance was relatively shorter than the wavelength. This limitation suggests that the motion amplification of the WEC due to the stationary wave may not have been fully realized within the tested distance range. Yang et al. [
6] assessed the hydrodynamic performance of WEC in intermediate water depth using Computational Fluid Dynamics (CFD). The study investigated how the performance of the WEC varied with changes in the distance between the breakwater and WEC over a wide range. Through this analysis, it was confirmed that the performance of the WEC can be improved by leveraging the effects of stationary waves, which are influenced by the presence of the breakwater.
Another approach to improve the efficiency of WEC is to choose the control of the PTO force. The latching control used in WEC was proposed by Budal and Falnes [
7]. It involves fixing the oscillating body when its velocity reaches zero, then releasing the body after a specific delay time when the motion of a WEC and the wave force are in a favourable phase. This control strategy aims to maximise the movement of the WEC. There are many control systems such as Declutching control and Latching control suggested by Babarit et al. [
8]. Research on latching control has commonly been conducted by analytical methods based on linear potential flow theory. The study by Ringwood and Butler [
9] proposed an optimised latching duration for regular and monochromatic waves, establishing a foundation for a constant latching duration without prediction of future incoming waves. This approach is particularly useful in investigations where wave predictions over time are not necessary, as in the case of regular wave studies. In a study by Giorgi and Ringwood [
10], the research delved into latching control strategies using OpenFOAM software (version 2.3) based on computational fluid dynamics. The outcome of this study facilitated the analysis of the nonlinear motion of WEC and the interpretation of WEC movements under the influence of latching control. The results revealed a pronounced manifestation of nonlinear effects, especially at the natural period of the WEC.
This study aims to devise a method to maximise power extraction from a WEC by leveraging latching control to enhance the motion of the system and capitalizing on the stationary wave effects generated from a vertical wall. Using CFD techniques, the research validates the proposed methodology through a verification process based on experimental results [
11] that include an existing Power Take-Off (PTO) system. The investigation involves CFD simulations to assess how the presence of a vertical wall, variations in the damping coefficient of the PTO, and the implementation of latching control influence the performance of the WEC. By systematically analysing these factors, the study aims to provide insights into how the power extraction efficiency can be maximized under different conditions. This research contributes to the understanding of WEC dynamics and lays the groundwork for optimizing the design and operation of wave energy conversion systems.
2. Geometry and Conditions
2.1. Target Wave Energy Converter
The focus of this investigation centres on a Wavestar-like wave energy converter (WEC) characterized as a pivoted point absorber. The Wavestar WEC comprises a buoy with a hemisphere shape, possessing a singular degree of freedom (DOF) in pitch motion, and incorporates a hydraulic power take-off (PTO) cylinder, as illustrated in . details the physical properties of the designated WEC. The buoy is configured with a pivotal point, denoted as point A, where an arm is connected, allowing for pitch motion along a fixed axis. The PTO cylinder’s displacement
Sc (
t), the distance between the moving point B and fixed point C, varies based on the WEC device’s position.
β(
t) is the angle between the WEC’s arm and the PTO, which will be discussed in more detail later when introducing a numerical PTO model.
. Schematic of the WEC (not at scale) including the centre of rotation (Point A) and the position of the hydraulic PTO cylinder (Point B and C).
. Physical properties of the target wave energy converter.
The numerical simulations were performed at 9 different wave conditions as detailed in , featuring varying wave periods ranging from 1.4 to 2.8 s. For the validation study, wave case 1 is selected for comparison with the experimental results [
11], which have been performed on a 1:5 scale model of the Wavestar WEC, and numerical results [
11,
12]. For the case study for this research, the wave height was 0.25 m, and the water depth was maintained at 3.0 m.
. Wave conditions, the wave conditions used for validation were marked in bold.
They should be described with sufficient detail to allow others to replicate and build on published results. New methods and protocols should be described in detail while well-established methods can be briefly described and appropriately cited. Give the name and version of any software used and make clear whether computer code used is available. Include any pre-registration codes.
3. Numerical Modelling
3.1. Governing Equations
The governing equations, including mass and momentum conservation, were solved using an unsteady Reynolds-Averaged Navier-Stokes (URANS) approach within the commercial CFD software Star-CCM+ (version 17.04). For unsteady, incompressible flows without body forces, the averaged continuity and momentum equations are represented in tensor notation and Cartesian coordinates as follows [
13]:
where $$\bar{\tau}_{ij}$$ represent the components of the mean viscous stress tensor, as indicated in Equation (2)
and $$\bar{p}$$ represents the mean pressure, $$\bar{\mathcal{u}}_i$$ refers to the averaged Cartesian components of the velocity vector, $$\rho\overline{u_l^{\prime}u_J^{\prime}}$$ denotes the Reynolds stresses,
ρ is the fluid density and
μ is the dynamic viscosity.
To solve the fluid flow in the computational domain, a RANS solver was employed using the finite volume method, which discretises the integral form of the governing equations. The continuity and momentum equations were solved sequentially through a predictor-corrector approach. A second-order upwind scheme was used for the spatial discretisation of convection and diffusion terms, while a second-order temporal discretisation was applied for time-dependent terms. The SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm was implemented to solve the pressure-velocity coupling.
For turbulence modelling, a realizable
k −
ε model was selected, which is widely used in numerical simulations in ocean engineering. The turbulence model also incorporates a two-layer approach, first proposed by Rodi [
14], to account for low Reynolds number meshes (with
y+~1) or wall-function meshes (with
y+ > 30). In this study, the Reynolds number varied between 1.5 × 10
6 and 3.4 × 10
6, placing the flow in a turbulent regime. To simulate the motion of the WEC under the influence of external wave forces and moments, the Dynamic Fluid Body Interaction (DFBI) scheme was applied, enabling the WEC to undergo pitch motion. The DFBI scheme calculates hydrodynamic forces and moments acting on the rigid body and solves the rigid body motion equations to predict its position at each time step.
Furthermore, the Volume of Fluid (VOF) technique, introduced by Hirt and Nichols [
15], was employed to represent the free surface, i.e., the air-water interface. This method captures the free surface around the WEC and models the regular waves within the computational domain.
3.2. Numerical Simulation Setup
3.2.1. Computational Domain and Boundary Conditions
The computational domain was constructed using STAR-CCM+, a commercial software package employing the Cartesian cut-cell method. The numerical simulation was conducted using a 1:5 scale model under the same conditions as the experiments [
11], and Froude similarity has been applied. In this research, two different computational domains were employed: One computational domain focused on simulating conditions without a vertical wall, while the other was taken account for the presence of a vertical wall. shows a present computational domain and selected boundary conditions for a simulation without a vertical wall. For a simulation case without the vertical wall, the WEC is positioned in the centre of the computational domain of 6
λ (
λ: wavelength) length, 1
λ width, 3 m water depth, and 3.75 m gap between the SWL and the top boundary. In order to avoid unnecessary numerical reflection from the boundary, wave-forcing scheme has been implemented as suggested and investigated thoroughly by several authors [
16,
17,
18,
19]. The length of the relaxation zone, where the wave forcing scheme is applied, is set to 2
λ, meeting the minimum requirement for the length of this zone. Notable, this zone is implemented in both the inflow and outflow areas of the simulation, the strength of the forcing coefficient, denoted as
f1, varies smoothly from zero to the maximum value at the boundary (See ). The optimum forcing coefficient
f1, as suggested by Perić and Abdel-Maksoud [
17], is derived from Equation (4).
. Present computational domain and boundary conditions for a simulation case without the vertical wall: (<b>a</b>) top view, (<b>b</b>) side view.
. Distribution of forcing strength for wave forcing scheme in the computational domain without vertical wall for T = 2.5 s.
To generate regular waves accurately and consistently throughout a calculation time, three types of refinement zones have been defined (See ). The first refinement zone has the same length as the computational domain and has above and below the SWL by the wave height of a wave case. The mesh resolution for the first refinement zone is set to 12 cells per wave height and over 100 cells per wavelength. The second refinement zone has the same length as the first zone but has a height twice that of the first zone. The mesh resolution for the second zone is 6 cells per wave height. The third refinement zone is centred around the buoy, with a length three times the buoy diameter and a width 1.5 times the diameter. This zone consists of the same grid resolution as the first zone per wave height.
The computational domain consists of a background mesh region and an overset mesh region. For the boundary conditions for the background mesh region, a velocity inlet boundary condition was established at the inflow boundary. This condition specifies the known distribution of velocity and fluid properties. The horizontal and vertical velocities, along with surface elevation for the inflow properties, were calculated using a fifth-order wave model proposed by Fenton [
20]. To reduce computational resources, a symmetry plane was placed at the centre of the buoy. At the outflow boundary, a pressure outlet condition was implemented. As for the buoy, a no-slip wall boundary condition was applied.
A dynamic overset mesh approach was employed to study the movements of the WEC model, enabling the accurate representation of its interactions with the surrounding fluids. To implement the overset mesh technique, a minimum of two different mesh regions was necessary. In this research, the computational domain included a background mesh region for simulating regular waves and an overset mesh region, which involved cutting a hole from the background mesh to simulate the body-fluid interaction. To ensure smooth interpolation of fluid data between the two mesh regions, it is essential to minimise the difference in mesh sizes for the corresponding meshes in both regions. Therefore, the size of the third refinement zone has been configured to sufficiently cover the overset mesh region, which moves in response to the motion of the WEC.
. Cells around the free surface and the distribution of cells along the z-direction: (<b>a</b>) Grid resolution in free surface, (<b>b</b>) Grid resolution around the buoy.
shows the distribution of forcing strength for the wave force scheme when a simulation case with a vertical wall. The boundary located in the x+ direction is subjected to a wall condition, and the WEC is positioned 3 metres away from this boundary. In this simulation case, the wave forcing scheme is applied to the inflow, and the thickness of the relaxation zone remains the same with the simulation case without the vertical wall. The length of the computational domain for the simulation case with the wall is 5
λ. Similar to the simulation case without the wall, the same three types of refinement zones have been established. It is highlighted that the size of the third refinement zone has been extended to the vertical wall. This extension is aimed at accurately capturing the wave runup at the vertical wall and the standing waves generated between the wall and the buoy. The numerical simulations were performed on a system equipped with Intel Xeon Gold 6138 (Skylake) processors operating at 2.0 GHz, utilizing 16 cores per simulation case through a High-Performance Computing (HPC) system. Each simulation case required approximately 1 to 3 days to complete.
. Distribution of forcing strength for wave forcing scheme in the simulation case with the vertical wall for T = 1.6 s.
3.2.2. Numerical PTO Model
In the study of Windt et al. [
11], the focus is on implementing resistive control in PTO model in order to matching the numerical result against their experimental data. The PTO torque is defined by Equation (5),
where
BPTO represents the angular damping constant, exerting a force opposite to the body’s angular velocity (
ωWEC). This damping force is associated with a resistive or dissipative effect, and it is directly linked to the WEC capacity to harness wave energy. Meanwhile,
KPTO denotes the rotational spring stiffness, representing a reactive force proportional to the rotational angle around a pivot point, typically negligible due to resistive control in the PTO system. Initially, an attempt was made to approximate PTO effects using an angular damping constant at the WEC’s pivot point, applying the theoretical PTO torque [
21,
22]. However, this simplified model fell short in accurately replicating the PTO system in the numerical simulation.
Consequently, as reported in the study by Windt et al. [
11], a more robust approach has been implemented. In this refined approach, the PTO force is now precisely applied to the WEC arm at the location of Point A. This adjustment aims to enhance the simulation’s accuracy, ensuring a more accurate representation of the actual physical system dynamics. A linear spring-damper system is implemented for the numerical PTO model (See Equation (6)).
The overall strategy of the numerical PTO model in this study followed the model presented by Windt et al. [
11]. The PTO force is modelled as a linear spring-damper system, which is defined in Dynamic fluid body interaction (DFBI) solver via a Point C, fixed throughout the simulation, and a Point B, moving with the buoy of the WEC. The DFBI solver can calculate the hydrodynamic forces and moments acting on the rigid body and solve the governing equations of the rigid body motion to determine the next position of the rigid body for the next time step. It is highlighted that the same calibrated coefficients of damping and stiffness were used in this study, as in Windt et al. [
11]. Since resistive control is employed in the Wavestar device, only damping and no reactive force should be applied by the PTO. However, an equivalent linear damping coefficient cannot lead to the expected results of their numerical simulation during a validation process against their experimental data. Similarly, Coiro et al. [
4] mentioned a mismatch between numerical results based on CFD and experiment results even though an equivalent linear damping coefficient has been applied in their PTO system. From the experiments by Windt et al. [
11], the inspection of the zero damping cases revealed that a PTO force was still being applied. It is concluded that the delays of the controller and hardware between target and actual force, in the physical tank, cause the residual reactive power. Another possible cause can be friction in the mechanical part. To overcome the gap between numerical simulation and experimental measurements, the calibration of the PTO coefficients is required. The numerical PTO coefficients of
BPTO and
KPTO can be achieved through a least square regression, with a detailed process available in the study of Windt et al. [
11]. The outcome of this process yields the following equations:
In order to accurately calculate the PTO force,
VPTO (
t) and
Sc (
t) must be determined precisely. Two straightforward methods are available for determining the velocity of PTO. The first method involves transforming the calculated angular velocity of the buoy, while the second method utilizes the rate of
Sc (
t). In the case of the second method, to calculate the velocity of PTO, a continuous time series of
Sc (
t) values is required, however, it yields a delay of one-time step. Although this approach may be simpler when the time step is very small, the first method is applied to mitigate potential errors associated with this delay. When the buoy of the WEC moves with a certain velocity, the angular velocity of WEC can be described as in the following equation:
where
V⊥ is cross-radial speed and
r is the length of a lever arm and all relevant parameters are depicted in . As point B is moving along the WEC motion, cross-radial speed of
VB at point B can be obtained by multiplying distance between point A and point B and the angular velocity of the buoy (see Equation (10)).
Point B, which the velocity of the PTO is implemented at, follows the movement of the WEC. Consequently, the velocity of the PTO device varies in accordance with
β(
t). The value of
β(
t) is determined along with geometrical transformations through the following equation:
Introducing a new local coordinate system with the x-axis aligned with segment AB and the origin at point B (See b, this coordinate system follows the motion of the WEC. The PTO force acting at point B in this coordinate system is expressed as follows:
In this study, an ideal PTO model is used, which does not account for losses such as friction, heat dissipation, or the dynamic system of the PTO. As a result, the absorbed power (
Pabs) and the generated power are assumed to be equal since no losses are considered. The absorbed power (
Pabs) can be expressed as:
Available power of a wave may be expressed as follows.
where
H is the wave height,
cg is the wave group velocity,
ρ is the water density and
g is the acceleration of gravity. The capture width ratio (CWR) is a non-dimensional performance ratio used to express the performance of a wave energy device. It is defined as the ratio of the absorbed power by the device (
Pabs) to the available wave power to the device (
Pwave) multiplied by the active width of the device (
widthactive) as shown in the following equation:
This non-dimensional parameter allows for consistent comparison of performance across different devices with different scaling ratios, as only the wave parameters need to be adapted correspondingly to the scaling ratio and site. In this study, the active width of the device is the same as the diameter of the buoy.
. Definition of variables for the numerical PTO model: (<b>a</b>) Variables for the buoy of the WEC movements, (<b>b</b>) Variables for PTO movements.
3.2.3. Latching Control
The purpose of the latching control strategy is to improve the efficiency of WECs by ensuring that the velocity is in phase with the excitation force. An example of operating latching control can be seen in . The device is stalled at time
t1,
t3 and
t5 where absolute value of displacement maximised, in other words when its velocity vanishes, and is held for a latched duration
TL. After the latched duration, the device is released at times
t2 and
t4. Ringwood and Butler [
9] have investigated the optimal latched duration for regular and monochromatic wave. When the wave period
TW exceeds the natural period of the device
Tn, the optimal calculation for a constant latched duration is as follows:
. Operation of latching control in present numerical simulation. Latching instants when the velocity is zero: <i>t</i><sub>1</sub>, <i>t</i><sub>3</sub> and <i>t</i><sub>5</sub>; latching duration: <i>T<sub>L</sub></i>; unlatching instants: <i>t</i><sub>2</sub> and <i>t</i><sub>4</sub>.
When the wave period is shorter than the natural period of device, an alternative latching control strategy can be considered to enhance the efficiency of a WEC system. This strategy includes options such as declutching [
8,
23], ramps with alternated maxima, and equal ending ramps [
24,
25]. The natural period of the device
Tn in Equation (18) does not account for the influence of damping on PTO.
illustrates the numerical latching control strategy through a logical flowchart. After the start of simulation, the latching control does not execute until
ttransition, which is approximately the time it takes for the buoy to reach a steady state. As mentioned earlier, the trigger of latching control occurs when the PTO velocity is zero. While it would be feasible with infinitely small-time steps, for discrete time step, finding the point where PTO velocity is exactly zero is challenging. Therefore, the time after the measured PTO velocity zero-crossed is defined as the starting point of the latching control. From this time onwards, the latching control becomes active, and
trelease is established. Afterward, if the latching control is already active, its continuation or termination is determined by comparing the current simulation time with
trelease.
Various methods exist for implementing a numerical model for the latching control strategy, but from a practical and efficient standpoint, two approaches seem prominent. The first method, often utilized in studies based on potential flow theory, involves the calculation of the damping by utilizing a function known as a damping profile, which represents the variation of the damping over time [
8,
23]. Alternatively, there is a method involving imposing constraints on the motion of the body to achieve effects similar to latching control [
10]. When using a damping profile, employing CFD becomes somewhat challenging as the damping coefficients need to be increased significantly in a short time for latching control to be active. Therefore, in this study, when latching control is active, constraints are applied to the body motion to observe its effects.
. Latching control strategy. Simulation time: <i>t<sub>sim</sub></i>; transition time: <i>t<sub>transition</sub></i>; latched duration: <i>T<sub>L</sub></i>; released instant: <i>t<sub>released</sub></i>.
4. Results
4.1. Verification and Validation
A similar verification and validation studies have been conducted in a prior investigation [
6], although this investigation focused on a different aspect and did not consider a PTO system. This current study introduces a numerical modeling of the PTO system, necessitating the validation of the present CFD model against experimental results.
To validate the numerical methods employed in this study, comparisons were made with experimental and numerical results from other studies which include experiments with a hydraulic Power Take-Off (PTO) [
11], numerical studies using the CFD-based OpenFOAM [
11], as well as the Boundary Element Method (BEM)-based ANSYS/AQWA software [
12].
The comparisons were carried out under identical wave conditions, specifically with a wave period of 1.4 s and a wave height of 0.1 m. Three different cases were considered for comparisons, which correspond to PTO damping values of 50, 100, and 200 Nms. illustrates the cylinder displacement for the case with PTO damping set to 50 Nms. Here, Experiment and Numerical 1 are the results from Windt et al. [
11] and Numerical 2 is the result from Ghafari et al. [
12]. Overall, the CFD results shows good agreement with experimental measurements, accurately capturing both peak and trough well.
In , the cylinder displacement is presented for the case with PTO damping set to 100 Nms. It is observed that the amplitude is slightly smaller compared to the case with PTO damping set to 50 Nm·s. Consequently, the CFD results shows a close match to the experimental data, while the numerical simulation based on the Boundary Element Method (BEM) predict somewhat lower values. For the case with PTO damping set to 200 Nms, as shown in , the displacement shows the smallest amplitude. The pattern is similar to the case with PTO damping set to 100 Nms.
Quantitative comparisons were made by recording the peaks and troughs over five cycles, calculating the average amplitude for each case. The results of these amplitude values are presented in . Overall, the CFD results consistently predicted values that closely approximated the experimental data.
. Comparison of cylinder displacement for validation (<i>B<sub>PTO</sub></i> = 50 Nms).
. Comparison of cylinder displacement for validation (<i>B<sub>PTO</sub></i> = 100 Nms).
. Comparison of cylinder displacement for validation (<i>B<sub>PTO</sub></i> = 200 Nms).
. Difference of cylinder displacement, PTO velocity and PTO force in the validation study.
4.1.1. Mesh
A mesh convergence study was conducted to optimise the mesh size, focusing on mesh size relative to both wave height and wavelength under selected wave conditions. Notably, our wave conditions range from 1.4 to 2.8 s, twice the difference between the shortest and longest wave conditions. This approach was adopted to avoid employing a fixed mesh size, which could result in an excessive number of unnecessary mesh elements. The determination of mesh size per wavelength and per wave height is crucial for enhancing the precision and efficiency of the computational model. For a mesh convergence study, the longest wave period in this research was selected and investigated. The minimum mesh size for z-direction is defined by the number of cells per wave height (CPH). Three mesh resolutions were investigated, where the number of CPH was doubled between each mesh configuration, with the number of CPH of 6, 8.5, and 12, respectively. For the number of cells per wavelength (CPL), there are two conditions to determine. Firstly, CPL must always be 100 or higher. Secondly, the mesh size for the x-direction is determined to be a multiple of 2
n of the mesh size for the z-direction. illustrates the cylinder displacement according to the mesh resolution. For the crest of the displacement, very little difference was observed between the three meshes, however, the result of the coarse mesh shows slight difference at troughs from the other two meshes, which are in good agreement with each other.
Consequently, the fine mesh, with 12 CPH, is used for all case study simulations. The total number of cells used ranges from 3.3 to 5.0 million cells, depending on the wave period. The determination of this cell count range is managed by the specific conditions of CPL according to wave period.
. Displacement variation for increasing mesh refinement.
4.1.2. Time Step
A time step of T/512 is used in all case study simulations. To find the time step for capturing both the wave generation within the background mesh and the dynamic interaction between the fluid and the body within the overset mesh is important. To ensure the fidelity of the simulations and meaningful interpretation of results, a thorough investigation and careful selection of the time step are imperative, aligning with the goals and intricacies of this study. Time step values of T/256, T/362, T/512, and T/724 are investigated, and the results are plotted in . The temporal convergence study adopts the finest mesh resolution determined in the mesh convergence study. From this analysis, a time step of T/512 was selected as the optimal choice.
. Cylinder displacement of the WEC for different time steps.
To examine how the vertical wall affects the results, two simulation cases were investigated: one with the vertical wall and the other without it. The results for the simulation without the vertical wall are presented first in Section 4.2.1, confirming the performance of the WEC model with PTO. Following that, the results of the simulation with the vertical wall are presented in Section 4.2.2, demonstrating the improvement of the performance of the WEC.
4.2.1. Case 1: Simulation without the Vertical Wall
Using the input wave series shown in , the PTO data (cylinder displacement, PTO velocity, and PTO force) and absorbed power obtained by the numerical PTO model have been compared for different damping coefficients The PTO data in , represent the mean height values, considering five consecutive peaks and troughs, and
Pabs does the averaged value during five consecutive wave periods. The table includes four different cases with different damping coefficient (
Bexp = 25, 50, 100, 200 Nms) obtained from Windt et al. [
11].
In , the time traces for PTO data and absorbed power are plotted for wave case 3 (T = 1.4 s and H = 0.25 m), which is the shortest wave period in this research. Analysing the displacement data reveals that as the damping coefficients increase, the amplitude of the displacement decreases. A similar trend is observed in the PTO velocity data. Conversely, the PTO force data exhibit an opposite trend to the displacement and PTO velocity data. Lastly, the absorbed power derived by the product of velocity and force, demonstrates a distinct pattern, recording high values when the damping coefficients are set to 50 and 100 Nms. It should be highlighted that maximising cylinder displacement, PTO velocity and force are not directly related to achieving optimal performance in absorbed power. The crucial factor for better performance is linked to the phase between PTO velocity and force, thus, the selection of the optimum damping coefficient is crucial to producing the higher absorbed power.
. Results of numerical simulations without a vertical wall for PTO data (displacement, PTO velocity, and force) and absorbed power according to damping coefficient, wave case 2 (T = 1.4 s).
In , the time traces for PTO data and absorbed power are depicted for wave case 5 (T = 1.8 s and H = 0.25 m). In a similar fashion of wave case 3, a comparative analysis of the PTO data and absorbed power is made based on the numerical PTO damping coefficients. In general, the cylinder displacement, PTO velocity, and force show similar behaviour to wave case 3, except for absorbed power. Particularly for wave case 5, the WEC device exhibits the most significant mean height value of cylinder displacement, presenting maximum motion across all wave cases. It is noteworthy that the natural period of this device, excluding the PTO system, approximates 1.9 s [
26]. Regarding absorbed power, an increase in the numerical PTO damping correlates with a decrease in the numerical PTO damping. The peak value is observed when the numerical PTO damping is 25 Nms.
. Results of PTO data, Power and CWR according to the wave cases and PTO damping coefficients without a vertical wall.
. Results of numerical simulations without vertical wall for PTO data (displacement, PTO velocity and force) and absorbed power according to damping coefficient, wave case 4 (T = 1.8 s).
For wave case 9, the PTO data and absorbed power show similar trend to the wave case 3, as illustrated in . The plotted time traces show relatively decreased amplitude of PTO data, with velocity amplitude for wave case 9 being approximately half of that observed in wave case 5. Consequently, low amplitude of PTO velocity and power results in low absorbed power regardless of the numerical PTO damping coefficients. shows the results of the PTO data, absorbed power and CWR according to the wave cases and PTO damping coefficients, including the calculated available wave power based on each wave case.
. Results of numerical simulations without a vertical wall for PTO data (displacement, PTO velocity, and force) and absorbed power according to damping coefficient, wave case 9 (T = 2.8 s).
In , the mean value of the cylinder displacement, PTO velocity, PTO force, and absorbed power are illustrated as a function of the wave period across various damping coefficients for the WEC. The mean values are determined using the same analytical approach as employed in the validation study. The figure includes different line colour and style representing damping coefficients ranging from 25 to 200 Nms.
It is evident from the graphs that the damping coefficients significantly influence the PTO data and absorbed power of the WEC. $$\bar{S}_{c}$$ is greatest with the lowest damping coefficient, and as the damping coefficient increases, $$\bar{S}_{c}$$ decreases. The damping coefficients of 25 and 50 Nms indicate a higher value of $$\bar{S}_{c}$$ near the natural period of the WEC, which is more evident with lower damping coefficients. On the other hand, with increasing damping coefficients, the change in $$\bar{S}_{c}$$ near the natural period the WEC becomes insignificant, indicating an overall reduction in $$\bar{S}_{c}$$ in each wave condition. This phenomenon aligns with general observations of increased damping in objects.
b shows the variation in $$\bar{V}_{PTO}$$ with respect to the wave period. Overall, it mirrors pattern observed in $$\bar{S}_{c}$$. However, a notable difference is that the wave period corresponding to the peak value of $$\bar{V}_{PTO}$$ decreases as the damping increases.
shows the displacement of the WEC as a function of wave period for different damping coefficients. The mean height of values is obtained in same analysis method as employed in the validation study. The different lines represent different damping coefficient from 25 to 200 Nms. The graphs show that the damping coefficient has a significant impact on the displacement, PTO velocity, PTO force and absorbed power of the WEC. $$\bar{S}_{c}$$ is greatest with the lowest damping coefficient, and as the damping coefficient increases, $$\bar{S}_{c}$$ decreases. The damping coefficients of 25 and 50 indicate a higher value of $$\bar{S}_{c}$$ near the natural period of the WEC, which is more evident with the smaller the damping coefficient. On the other hand, as the damping coefficient increases, the change in the $$\bar{S}_{c}$$ is insignificant in the vicinity of the natural period, and it can be seen that the overall response of $$\bar{S}_{c}$$ according to the wave case becomes smaller. This is a general phenomenon that occur as the damping of an object increase.
b shows the change in $$\bar{V}_{PTO}$$ as a function of wave period. Overall, it shows a similar pattern to the change in $$\bar{S}_{c}$$. The peak value of $$\bar{V}_{PTO}$$ when
BPTO = 25 Nms is observed at
T = 1.8 s. As damping coefficient increases, overall magnitude of $$\bar{V}_{PTO}$$ decreases, and the gap between its maximum and minimum value of $$\bar{V}_{PTO}$$ narrows. Moving on the c, it shows the variation of $$\bar{F}_{PTO}$$ with respect to the wave period. The damping coefficient increases, there is a decrease in the overall magnitude of $$\bar{F}_{PTO}$$. The overall magnitude is obviously correlated with the
BPTO rather than the magnitude of $$\bar{S}_{c}$$ and $$\bar{V}_{PTO}$$. d illustrates the results of
Pabs in relation to the wave period.
Generally, but in the case of $$\bar{S}_{c}$$, it can be seen that the wave period in which the maximum value of $$\bar{V}_{PTO}$$ appears decreases as the damping increases, whereas in the case of $$\bar{S}_{c}$$, the peak value is mainly shown near the natural period.
. Comparison of numerical results for Case study 1: Simulation without a vertical wall according to different wave periods and PTO damping coefficients ((<b>a</b>): mean height of cylinder displacement, (<b>b</b>): mean height of PTO velocity, (<b>c</b>): mean height of PTO force, (<b>d</b>): averaged absorbed power, (<b>e</b>): CWR).
4.2.2. Case 2: Simulation with the Vertical Wall
In this chapter, simulation results under the condition of a vertical wall were compared using the same methodology as in the previous case of simulation without the vertical wall and a comparative analysis between Case 1 and Case 2 has also been included.
illustrates the displacement, PTO velocity, force, and power results of the WEC with respect to PTO damping under the presence of the vertical wall. As observed in the results, similar to the case without the vertical wall, the amplitude of PTO displacement gradually decreases with an increase in PTO damping. The overall trend of the time-traced results closely resembles that of Case 1, with the only difference being the amplitude variation.
. Results of numerical simulations without a vertical wall for PTO data (displacement, PTO velocity and force) and absorbed power according to damping coefficient, wave case 6 (T = 2.0 s).
illustrates the performance of the WEC when installed on a vertical wall, while lists detailed numerical values. The results vary with the wave period and PTO damping, generally showing a significant motion response and an absorbed power when the wave period is between 2 and 2.2 s. Despite the occurrence of stationary wave phenomena around the WEC due to the presence of the vertical wall, the predominant influence is demonstrated by the motion induced by the WEC’s characteristic of the natural period. In e, a sudden change in values is observed when the wave period is 1.8 s compared to periods of 1.6 s or 2 s. This abrupt change is attributed to the positioning of the WEC buoy near the vertical wall. The presence of a vertical wall induces a stationary wave effect around the WEC buoy, leading to the phenomenon of reduced wave height at specific locations. Furthermore, the area around the WEC buoy is expected to exhibit complex wave pattern due to the coexistence of incident and reflected waves, as well as waves generated by the WEC buoy and its corresponding reflected waves. It is highlighted that CWR exceeds 1.0, which is attributed to the high absorbed power resulting from the stationary wave effect. Additionally, in the absence of a vertical wall, low CWR was predicted for PTO damping values of 100 or 200 Nms. However, with the presence of a vertical wall, it is noteworthy that a significantly respectable CWR was recorded even with high PTO damping. However, even with the presence of the vertical wall, low CWR values were recorded for all PTO damping values when the wave period was 2.8 s.
compares the CWR under the same PTO damping values, with a focus on the presence or absence of the vertical wall. A comparison of results for the case where PTO damping is at its minimum value of 25 Nms can be seen in a. The most significant difference is observed in the wave period range of 1.8 s to 2.2 s, which corresponds to the natural period of the WEC buoy. As the PTO damping increases, it can be observed that in the case of no vertical wall, the wave period at which CWR exhibits its peak gradually shifts towards shorter periods. On the other hand, in the presence of the vertical wall, regardless of changes in PTO damping, the peak of CWR mostly occurs when the wave period is around 2 s. This indicates that adjusting the spacing between the vertical wall and the buoy appropriately and utilizing stationary wave near the buoy effectively, it can be an effective method to enhance CWR.
. Comparison of numerical results for Case study 2: Simulation with vertical wall according to wave period and PTO damping coefficient ((<b>a</b>): mean height of cylinder displacement, (<b>b</b>): mean height of PTO velocity, (<b>c</b>): mean height of PTO force, (<b>d</b>): averaged absorbed power, (<b>e</b>): CWR).
. Result of PTO data, Power and CWR according to wave case and damping coefficients for the cases with the vertical wall.
. Comparison of CWR based on the presence of absence of the vertical wall ((<b>a</b>): <i>B<sub>PTO</sub></i> = 25 Nms, (<b>b</b>): <i>B<sub>PTO</sub></i> = 50 Nms, (<b>c</b>): <i>B<sub>PTO</sub></i> = 100 Nms, (<b>d</b>): <i>B<sub>PTO</sub></i> = 200 Nms).
4.2.3. Case 3: Simulation without Vertical Wall and under Latching Control
In this section, the results are presented under the condition of the absence of a vertical wall and the introduction of latching control. These results are compared with a corresponding case (Case 1) where there is no vertical wall but with no latching control, establishing a basis for the comparison between the two scenarios.
displays the time-dependent results of PTO displacement, velocity, force, and power for wave periods of 2.8 s, considering PTO damping values of 25 and 50 Nms. It can be observed that latching control initiates after 8.5 s when the buoy’s velocity becomes zero. Once latching control begins, the displacement gradually increases and exhibits periodic variations after approximately two cycles. The constant latching duration is determined by Equation (18), and it can be verified from the graph that there is no change in displacement during this constant latching duration. After the constant latching duration has elapsed, it can be confirmed that the WEC buoy is released. Following this release, it is evident from the graph that there is a steeper change or slope in displacement compared to the scenario where the latching control was not applied. Not only in displacement but also in velocity and force, similar patterns are observed. Additionally, due to the improvement in PTO velocity and force induced by latching control, it can be confirmed that the peak of power is elevated.
. Results of numerical simulations without vertical wall under latching control for PTO data (displacement, PTO velocity and force) and absorbed power according to damping coefficient, wave case 9 (T = 2.8 s).
presents the results when latching control is employed without a vertical wall, along with the PTO displacement, velocity, and force, absorbed power, and CWR results for Case 1. Since Equation (18) is valid under the condition where the wave period of the incident wave is greater than the natural period of the object, this study only presents results for wave periods of 2.2, 2.5, and 2.8 s. The implementation of latching control leads to an increase not only in displacement but also in velocity, force, and absorbed power. Consequently, there is a substantial improvement in CWR. In case without latching control, CWR recorded values below 0.2 for long wave periods. However, with the introduction of latching control, a notable effect was observed, with CWR exceeding 0.4 across all wave period conditions. The numerical results for the case with latching control, as depicted in , can be seen in .
. Comparison of numerical results for Case study 3: Simulation without vertical wall and latching control according to wave period and PTO damping coefficient ((<b>a</b>): mean height of cylinder displacement, (<b>b</b>): mean height of PTO velocity, (<b>c</b>): mean height of PTO force, (<b>d</b>): averaged absorbed power, (<b>e</b>): CWR).
. Result of PTO data, Power and CWR according to wave case and damping coefficients for the cases without the vertical wall and latching control.
4.2.4. Case 4: Simulation with Vertical Wall and under Latching Control
The previous chapter examined the changes in the performance of the WEC upon the introduction of latching control (Case 3). In this section, not only the effects of latching control but also the synergistic effects when a vertical wall is present alongside latching control in the WEC are investigated.
illustrates the results of simulations with both the vertical wall and latching control when the wave period is 2.2 s. It displays the time-dependent PTO displacement, velocity, force, and absorbed power. There does not appear to be a significant overall difference in PTO displacement, velocity, force, and absorbed power with varying PTO damping compared to the previous case.
From around 7 s in the simulation, latching control initiates. Despite the PTO displacement not showing significant changes for
BPTO = 25 Nms, there is a slight increase in the maximum and minimum values of velocity. This impact ultimately leads to higher power, and as a result, an increase in CWR. These results can be seen in .
Due to the effects of latching control, similar to Case 3, there is a relatively improved performance in the long-wave period range (T = 2.5 s and 2.8 s), resulting in enhanced absorbed power and CWR. Additionally, even in the case with a vertical wall at T = 2.2 s yields a CWR exceeding 1, the introduction of latching control further improves the performance. Detailed numerical results can be found in .
. Results of numerical simulations without vertical wall under latching control for PTO data (displacement, PTO velocity and force) and absorbed power according to damping coefficient, wave case 7 (T = 2.2 s).
. Result of PTO data, Power and CWR according to wave case and damping coefficients for the cases with the vertical wall and under latching control.
. Comparison of numerical results for Case study 4: Simulation with a vertical wall and under latching control according to wave period and PTO damping coefficient ((<b>a</b>): mean height of cylinder displacement, (<b>b</b>): mean height of PTO velocity, (<b>c</b>): mean height of PTO force, (<b>d</b>): averaged absorbed power, (<b>e</b>): CWR).
To examine the effect of the vertical wall in the presence of latching control, Case 3 and Case 4 results are compared, as shown in . With a PTO damping of 25 Nms and a wave period of 2.2 s, it can be observed that the presence of the vertical wall increases CWR from 0.72 to 1.20. Furthermore, with a PTO damping of 50 Nms, an even larger increase from 0.62 to 1.43 is noted. As the wave period increases, it can be observed that the magnitude of the CWR variation due to the vertical wall gradually decreases. Additionally, without a vertical wall, the change in CWR with respect to the wave period is small, while with the vertical wall, the variation in CWR with the wave period is more pronounced.
Figure 25. Comparison of CWR for different wave periods with and without the vertical wall and various PTO damping values.
5. Conclusions
This study focused on the analysis of a pivoted point absorber-type WEC using numerical simulations with CFD to assess its performance. It examined the WEC’s performance under various conditions, particularly the presence of a vertical wall and the application of latching control across different wave periods and PTO damping forces. Building on previous research that explored the hydrodynamic performance of WECs based on the distance between the vertical wall and WEC, this study introduced a numerical PTO design to validate the WEC’s performance.
Star-CCM+ was utilized as the CFD software, and a wave-forcing scheme was implemented to ensure stable numerical results, optimizing computation time. In order to apply the numerical PTO model in Star-CCM+, modifications were made to the 1-D linear spring-damping system, and the latching control algorithm was adapted. Verification and validation processes were conducted to confirm the accuracy of the computational domain. Comparison with experimental measurements and other numerical simulations revealed minimal discrepancies, confirming the reliability of the numerical model.
The results indicated that for shorter wave periods of 2 s and 2.2 s, the WEC achieved a high Capture Width Ratio (CWR) regardless of the PTO damping force. For longer wave periods (2.5 s and above), the presence of the vertical wall had minimal impact on the CWR, resulting in lower values. The study also demonstrated that latching control significantly enhanced the WEC’s performance, particularly in the long-wave period range. The application of latching control led to consistently improved CWR, especially in conditions where the wave period exceeded the natural period of the WEC. This indicates the effectiveness of latching control for optimizing WEC performance in these conditions. Additionally, the analysis of the effects of the vertical wall during latching control revealed that the highest CWR was achieved at a wave period of 2.2 s, highlighting a synergistic interaction between the vertical wall and latching control. This combination showed the greatest performance enhancement for shorter wave periods. However, as the wave period increased, the influence of the vertical wall became negligible.
In summary, this study has demonstrated that the combination of a vertical wall and latching control can significantly enhance WEC performance, particularly for short to moderate wave periods, while the influence of the vertical wall diminishes at longer wave periods.
Acknowledgments
Results were obtained using the ARCHIE-WeSt High Performance Computer (www.archie-west.ac.uk) based at the University of Strathclyde.
Author Contributions
Conceptualization, I.Y.; Methodology, I.Y.; Software, I.Y.; Validation, I.Y., and A.I.; Formal Analysis, I.Y.; Investigation, I.Y. and A.I.; Resources, I.Y. and A.I.; Data Curation, I.Y.; Writing—Original Draft Preparation, I.Y.; Writing—Review & Editing, I.Y., M.T., T.T. and A.I.; Visualization, I.Y.; Supervision, M.T., T.T. and A.I.; Project Administration, I.Y., M.T., T.T. and A.I.; Funding Acquisition, T.T. and A.I.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
This research received no external funding.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
References
1.
Mustapa MA, Yaakob OB, Ahmed YM, Rheem C-K, Koh KK, Adnan FA. Wave energy device and breakwater integration: A review.
Renew. Sustain. Energy Rev. 2017,
77, 43–58. doi:10.1016/j.rser.2017.03.110.
[Google Scholar]
2.
Zhao XL, Ning DZ, Zou QP, Qiao DS, Cai SQ. Hybrid floating breakwater-WEC system: A review.
Ocean Eng. 2019,
186, 106126. doi:10.1016/j.oceaneng.2019.106126.
[Google Scholar]
3.
Ning D-Z, Zhao X-L, Zhao M, Hann M, Kang H-G. Analytical investigation of hydrodynamic performance of a dual pontoon WEC-type breakwater.
Appl. Ocean Res. 2017,
65, 102–111. doi:10.1016/j.apor.2017.03.012.
[Google Scholar]
4.
Coiro DP, Troise G, Calise G, Bizzarrini N. Wave energy conversion through a point pivoted absorber: Numerical and experimental tests on a scaled model.
Renew. Energy 2016,
87, 317–325. doi:10.1016/j.renene.2015.10.003.
[Google Scholar]
5.
Reabroy R, Zheng X, Zhang L, Zang J, Yuan Z, Liu M, et al. Hydrodynamic response and power efficiency analysis of heaving wave energy converter integrated with breakwater.
Energy Convers. Manag. 2019,
195, 1174–1186. doi:10.1016/j.enconman.2019.05.088.
[Google Scholar]
6.
Yang I, Tezdogan T, Incecik A. Numerical investigations of a pivoted point absorber wave energy converter integrated with breakwater using CFD.
Ocean Eng. 2023,
274, 114025. doi:10.1016/j.oceaneng.2023.114025.
[Google Scholar]
7.
Budal K, Falnes J. Interacting Point Absorbers with Controlled Motion; Power from Sea Waves: Edinburgh, UK, 1980.
8.
Babarit A, Guglielmi M, Clément AH. Declutching control of a wave energy converter.
Ocean Eng. 2009,
36, 1015–1024. doi:10.1016/j.oceaneng.2009.05.006.
[Google Scholar]
9.
Ringwood J, Butler S. Optimisation of a wave energy converter.
IFAC Proc. Vol. 2004,
37, 155–160. doi:10.1016/S1474-667031724-X.
[Google Scholar]
10.
Giorgi G, Ringwood JV. Implementation of latching control in a numerical wave tank with regular waves.
J. Ocean Eng. Mar. Energy 2016,
2, 211–226. doi:10.1007/s40722-016-0052-8.
[Google Scholar]
11.
Windt C, Davidson J, Ransley EJ, Greaves D, Jakobsen M, Kramer M, et al. Validation of a CFD-based numerical wave tank model for the power production assessment of the wavestar ocean wave energy converter.
Renew. Energy 2020,
146, 2499–2516. doi:10.1016/j.renene.2019.08.059.
[Google Scholar]
12.
Ghafari HR, Ghassemi H, He G. Numerical study of the Wavestar wave energy converter with multi-point-absorber around DeepCwind semisubmersible floating platform.
Ocean Eng. 2021,
232, 109177. doi:10.1016/j.oceaneng.2021.109177.
[Google Scholar]
13.
Ferziger JH, Perić M, Street RL. Computational Methods for Fluid Dynamics; Springer: Berlin, Germany 2002; Volume 3.
14.
Rodi W. Experience with two-layer models combining the k-epsilon model with a one-equation model near the wall. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1991. doi:10.2514/6.1991-216.
15.
Hirt CW, Nichols BD. Volume of fluid (VOF) method for the dynamics of free boundaries.
J. Comput. Phys. 1981,
39, 201–225. doi:10.1016/0021-999190145-5.
[Google Scholar]
16.
Peric R. Minimizing Undesired Wave Reflection at the Domain Boundaries in Flow Simulations with Forcing Zones. Doctoral Dissertation, Technischen Universität Hamburg, Hamburg, Germany, 2019.
17.
Perić R, Abdel-Maksoud M. Reliable damping of free-surface waves in numerical simulations.
Ship Technol. Res. 2016,
63, 1–13. doi:10.1080/09377255.2015.1119921.
[Google Scholar]
18.
Perić R, Vukčević V, Abdel-Maksoud M, Jasak H. Optimizing wave generation and wave damping in 3D-flow simulations with implicit relaxation zones.
Coast. Eng. 2022,
171, 104035. doi:10.1016/j.coastaleng.2021.104035.
[Google Scholar]
19.
Kim J, O’Sullivan J, Read A. Ringing Analysis of a Vertical Cylinder by Euler Overlay Method. Volume 4: Offshore Geotechnics. In Proceedings of the Yeung Honoring Symposium on Offshore and Ship Hydrodynamics; Ronald W, Ed.; American Society of Mechanical Engineers: New York, NY, USA, 2012.
20.
Fenton JD. A Fifth-Order Stokes Theory for Steady Waves.
J. Waterw. Port Coast. Ocean Eng. 1985,
111, 216–234.
[Google Scholar]
21.
Penalba M, Davidson J, Windt C, Ringwood JV. A high-fidelity wave-to-wire simulation platform for wave energy converters: Coupled numerical wave tank and power take-off models.
Appl. Energy 2018,
226, 655–669. doi:10.1016/j.apenergy.2018.06.008.
[Google Scholar]
22.
Zurkinden AS, Ferri F, Beatty S, Kofoed JP, Kramer MM. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter.
Ocean Eng. 2014,
78, 11–21. doi:10.1016/j.oceaneng.2013.12.009.
[Google Scholar]
23.
Teillant B, Gilloteaux JC, Ringwood JV. Optimal Damping Profile for a Heaving Buoy Wave Energy Converter.
IFAC Proc. Vol. 2010,
43, 360–365. doi:10.3182/20100915-3-de-3008.00067.
[Google Scholar]
24.
Babarit A, Duclos G, Clément AH. Comparison of latching control strategies for a heaving wave energy device in random sea.
Appl. Ocean Res. 2004,
26, 227–238. doi:10.1016/j.apor.2005.05.003.
[Google Scholar]
25.
Babarit A, Clément AH. Optimal latching control of a wave energy device in regular and irregular waves.
Appl. Ocean Res. 2006,
28, 77–91. doi:10.1016/j.apor.2006.05.002.
[Google Scholar]
26.
Jakobsen MM, Beatty S, Iglesias G, Kramer MM. Characterization of loads on a hemispherical point absorber wave energy converter.
Int. J. Mar. Energy 2016,
13, 1–15. doi:10.1016/j.ijome.2016.01.003.
[Google Scholar]