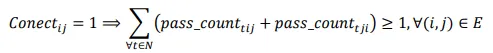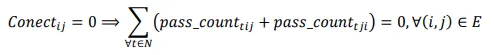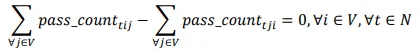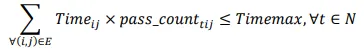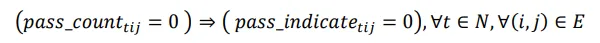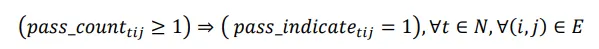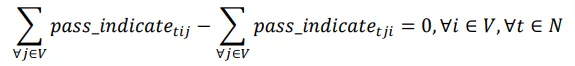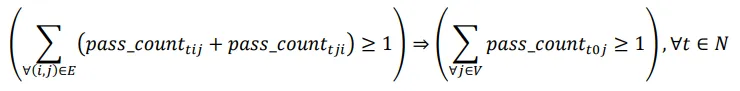1. Introduction
Security guards are entrusted with the critical task of patrolling facilities, both internally and externally, and promptly reporting any suspicious activity. These duties are physically and mentally demanding, and can on occasion be hazardous. Furthermore, security guards frequently work night shifts and extended hours. As a consequence of these factors, the security industry is grappling with a labor shortage. Additionally, the industry faces the challenge of rising labor costs [
1]. For instance, Ritsumeikan University spends a staggering 120 million yen annually on security alone [
2]. Drones present a promising solution to address these issues. Drones offer several advantages over traditional human patrols. Firstly, their integrated cameras allow for real-time monitoring, enabling immediate detection of anomalies [
3]. Secondly, they provide access to hazardous or difficult-to-reach areas [
4]. Additionally, initiatives to utilize drones for security patrols are gaining traction in Japan, as evidenced by demonstration tests conducted by ALSOK [
5]. One key challenge associated with drone deployment is their limited battery capacity, restricting their flight duration [
6]. Consequently, efficient surveillance routes must be pre-determined, considering the maximum flight time.
The Drone Arc Routing Problem (DARP), an extension of the Arc Routing Problem (ARP), is a common approach to optimizing drone patrol routes [
7]. Unlike the node routing problem that focuses on services performed node, ARP focuses on services performed along network edges [
8].
Previous studies have explored various aspects of drone-based security patrols. In [
9], a Vehicle-Drone Arc Routing Problem (VD-ARP) was introduced, combining vehicles and drones for urban traffic patrols, aiming to minimize total patrol time while considering drone flight time. However, this approach faces limitations due to the high cost of vehicles and their unsuitability for indoor facility patrols. Another study [
10] addressed facility patrolling and guarding using drones, proposing a method to minimize the number of drones with flexible drone starting points. However, this method suffers from NP-hardness, making it unsuitable for large-sized problems.
This paper presents an extension of the method proposed in [
10] that addresses its limitations.
The contributions of this paper are threefold: (1) We first define the problem of determining surveillance routes with a minimum number of drones; (2) We formulate the problem as an integer linear program (ILP), enabling the exploration of optimal solutions; (3) We develop a heuristic algorithm to efficiently solve large-scale instances of the problem. We then compare the performance of our heuristic with the ILP-based approach through comprehensive experimental results.
The structure of this paper is as follows: Section 2 describes the literature review. Section 3 describes the ILP-based method and the greedy method. Section 4 describes the experimental methods, results, and discussion. Section 5 describes the overall summary and future work.
2. Related Work
2.1. Arc Routing Problem
The research on the arc routing problem (ARP) has a history dating back to the 18th century with the famous “seven bridges” problem posed by Swiss mathematician Leonhard Euler. The field of modern ARP research gained significant momentum in the 1960s when Chinese mathematician Meigu Guan introduced the “Chinese Postman Problem” (CPP) [
8]. Guan [
11] addressed the optimization of mail carrier routes. Here, mail carriers are assigned a set of street segments, and the goal is to find the shortest walking distance that allows them to visit all assigned segments and return to the post office. Another key variant of ARP is the “Rural Postman Problem” (RPP), which focuses on optimizing mail delivery routes that only utilize a portion of the road network [
8]. Branch-and-bound algorithms were employed to tackle the classical RPP, as demonstrated in [
12]. Furthermore, [
13] explored the use of large-sized neighborhood search algorithms to solve RPPs with time windows. Since the 1980s, the field of ARP research has seen significant growth. Researchers have explored various extensions and new problem formulations to model real-world applications more accurately and optimize diverse objectives beyond just route length. These extensions include Periodic Arc Routing Problems (PARPs) [
14,
15], ARPs with profits [
16,
17], and Location Arc Routing Problems (LARPs) [
18,
19].
PARPs refer to a problem where service needs to be repeated at each edge for some period of time (e.g., days) on a time horizon (e.g., weeks or months). The objective is to design efficient routes for each service period within the horizon, ensuring all service requirements are met while minimizing the total cost. In [
14], the authors consider the problem of road maintenance and network monitoring. Each road segment has a specific monitoring requirement based on traffic volume. The paper proposes a mathematical model and a heuristic algorithm to determine flight routes that fulfill the required frequency of passing each road.
Unlike regular ARPs, ARPs with profits focus on maximizing gains by strategically selecting only the most “valuable” edges to service. Profits increase with the value of serviced edges, but neglecting them incurs penalties. [
16] explores a scenario where a single company vehicle services a network of edges, with the option to outsource servicing for some edges. The paper proposes a refined tabu search algorithm combined with an ILP model. This hybrid approach aims to minimize the total cost, which includes the sum of services performed by both the in-house vehicle and outsourced services represented as penalty costs.
LARPs extended traditional ARPs by incorporating facility location decisions. In addition to finding the optimal flight route for a vehicle, LARPs also determine the ideal location for a facility, such as a vehicle depot. This problem can be optimized for various objectives, including minimizing the total cost or the length of the longest route or maximizing the total benefit from servicing each edge. Additionally, factors like fixed costs for vehicles and facility setup, as well as facility capacity, can be considered. For example, [
18] explores the problem of using electric vehicles for waste collection, where service needs to be provided at each edge. The paper proposes various optimization methods, including ILP models, genetic algorithms, and grey wolf optimizers, to determine the optimal locations for charging stations, dynamic charging arcs, and waste collection centers, along with the most efficient routes for the vehicles.
Recent research has focused on the Drone Arc Routing Problem (DARP), an extension of ARP for drone applications.
2.2. Drone Arc Routing Problem
With the widespread use of drones, traditional research on ARP has expanded. The extension of ARP to the drone problem is called DARP, first introduced in [
7]. DARP focuses on optimizing drone-based services (e.g., imaging, inspections, surveillance) delivered to edges within a network (e.g., pipelines, roads, railways). In DARP scenarios, drones operate with limited flight times due to battery constraints.
DARP research encompasses various applications, including patrolling tasks [
9,
10,
20,
21,
22,
23,
24] and inspections [
25,
26].
Traffic monitoring through drone patrols has been a well-researched area within DARP regard of patrol. Studies like [
9,
20,
21,
22,
23,
24] propose a coordinated vehicle and drone for urban traffic patrol scenarios. This combined approach helps address the inherent battery limitations of drones. [
20] employs mixed integer linear programming and a branch-and-cut algorithm for efficient problem-solving. [
21] investigate a two-tier cooperative routing approach for a single ground vehicle and a single drone. [
22] proposes an algorithm for coordinating one vehicle and multiple drones during wide-area inspections. [
9] utilizes a large neighborhood search algorithm to tackle the problem. [
23] introduces a hybrid optimization algorithm that combines randomized variable neighborhood descent search and simulated annealing. [
24] explores two-stage heuristic solution approaches for this scenario.
While research on combined vehicle-drone patrols is abundant, challenges remain. Vehicles can be expensive and unsuitable for indoor environments like facilities. To address these limitations, [
10] proposes a stand-alone drone solution for facility surveillance patrols. This method focuses on minimizing the number of drones. However, [
10] faces limitations when handling large-sized problems. To overcome this, we propose a greedy method as an extension, specifically designed to tackle large-sized facility patrols.
3. Proposed Methods
3.1. Problem Definition
This paper addresses the problem of finding the minimum number of drones required for efficient surveillance routing. We assume that:
• Drones must return to their departing point within their maximum flight time.
• A single, fixed departing point (point “0”) exists.
• Every aisle must be passed by at least one drone.
Figure 1a shows an example problem. Each node (0, 1, 2, 3) indicates points, and each point is connected to at least one other point via an aisle. The time required to pass each aisle is also displayed. Figure 1b illustrates the minimum-drone flight route for patrolling this example problem, with a total surveillance time of 80 seconds. The specific route is (0)-(1)-(2)-(0)-(3)-(2)-(0). Figure 1c demonstrates the flight route for the same example problem using two pre-assigned drones. In this case, both drones require 40 seconds for surveillance.
As demonstrated in Figure 1b and c, utilizing more drones can reduce surveillance time. While deploying fewer drones, it remains possible to complete the task within the flight time limit. Since drones are expensive, minimizing the number of required units is crucial.
Figure 1. (a) Example problem; (b) Flight route when there is only one drone; (c) Flight route when there are two drones (red and blue).
This section describes the mathematical model proposed in [
9]. We introduce additional constraints to ensure a fixed departing point “0”. This model can be solved by general-purpose ILP solver software. The surveillance network is represented by undirected graphs denoted by G = (V, E) A set of points of G is denoted as V = {0, 1 ,…, Point}, where “
Point” is the number of points. A set of aisles of G is defined as E = {e
ij = (i,j)│i,j ∈ V}, where e
ij represents the aisles from points i to j. A set of drones is denoted as N = {t│1 ≤ t ≤ Num_max}, where Num_max is the maximum number of drones. Table 1 represents the notations for this paper.
The objective function of this paper consists of Formula (1). This formula facilitates the minimization of the number of drones.
In addition, the constraints that the problem should satisfy are as follows.
Constraint (2) guarantees that every aisle between points
i and
j is passed by at least one drone if there is a connection between these points.
Constraint (3) prohibits any drone from traveling that non-existent aisle if there is no aisle connecting points
i and
j.
Constraint (4) prevents a drone from remaining stationary at the same point for the entire duration.
Constraint (5) ensures that for each point and each drone, the number of times the drone enters the point equals the number of times it exits.
Constraint (6) indicates that the flight time of each drone is within the maximum value.
Constraints (7) and (8) show the relationship between “
pass_counttij” and “
pass_indicatetij”
Constraint (9) guarantees that the route will be a circuit.
Constraints (10) and (11) indicate that the
dronet = 1 if each aisle is passed by drone
t, and
dronet = 0 if not. These constraints allow us to isolate the element of edge
eij from the objective function, thereby enabling the appropriate determination of the minimum number of drones required.
Constraint (12) guarantees that the
dronet used will always depart from point “0”.
3.3. Greedy Method
While the ILP-based method introduced in Section 3.2 offers an optimal solution, it can become computationally expensive for large-sized problems. This section presents the greedy method as an alternative approach for handling such scenarios. The greedy method is a well-established approach in combinatorial optimization, known for its simplicity and ease of implementation [
27]. However, it prioritizes locally optimal choices at each step, potentially leading to solutions that may not be the absolute optimum for the entire problem [
28]. To address large-sized problems efficiently, the greedy method was chosen due to its lower computational complexity and ease of implementation, even though it may not always find the absolute optimal solution.
Algorithm 1 presents the pseudo-code for the greedy method. The term “
iterable” denotes a list, while “
element” signifies its constituent parts. These terms are employed during the definitions of the “
not any” and “
all” functions. “
drone_num_max” indicates the maximum number of drones. “
drone_num” indicates how many drones this is.
current_point[drone_num] indicates the point where the drone is currently located.
unvisited[current_point[drone_num]] indicates the set of unvisited points from the point.
time[current_point[drone_num]][point] shows the time it takes to pass from the “
current_point” to the “
point”.
count_visited_points[drone_num][current_point[drone_num]][point] shows the number of times each drone has passed each aisle.
fly_time[drone_num] indicates the total flight time of each drone. “
goal_point” indicates the goal point of the drone.
The 1–7 lines define the “
not any” function, which is used on line 25. In this paper, “
not any” returns True if all “
element” of the “
iterable” are False. Lines 8–14 define the “
all” function, which is used on line 35. In this paper, “all” returns True if all “
element” of the “
iterable” are True. Lines 15–40 show loops that iterate over each maximum number of drones. In lines 18–29, the route selection is repeated until there are no more unvisited points. Lines 20–24 differentiate between the cases when there are and are not unvisited points from the current point. If there are unvisited points, the point with the shortest flight time is selected as the next point (20–21). If there are no unvisited points, the point with the shortest flight time among the aisles with the fewest visits is selected as the next point (22–24). Lines 25–27 indicate that the “
loop_unvisited” should be exited if there are no unvisited points. In lines 31–33, the route selection is repeated until the goal point is reached. In this case, the point with the shortest flight time among the aisles with the fewest visits is selected as the next point. In lines 35–39, the case is divided based on whether the total flight time of each drone exceeds the maximum value. If the total flight time of each drone does not exceed the maximum value, the “
loop_drone_num_max” is terminated, and the route discovered at that time is determined as the flight route. If the maximum value is exceeded, as indicated in line 38, the maximum number of drones is increased by one, and the process restarts from line 15. The time complexity of the greedy method proposed in this paper is
O(
N3 ×
E ×
V), where
V is the number of points,
E is the number of aisles, and
N is the maximum number of drones.
4. Experiments
4.1. Synthetic Maps
This section describes the experimental setup used to evaluate the performance of the ILP-based and greedy methods and presents the results obtained.
4.1.1. Setup
We generate benchmark problems for evaluating our proposed methods. The dataset consists of 60 randomly generated undirected graphs, where drones can pass between aisles in any direction. Each problem instance varies in size from 10 to 15 points, with 10 problems generated for each point size. The coordinates of each point are randomly determined. We use incomplete graphs, where not all pairs of points are necessarily connected by an aisle. The number of aisles connected to each point is set to approximately 50% of the number in a complete graph. The travel time between any two points is set within a range of 9 to 180 seconds. We set the parameters for the drones. The maximum flight time of a drone is set to 1200 seconds, and we consider up to 10 drones for each problem. The ILP-based method was solved by IBM ILOG CPLEX Optimizer Studio 20.1.0 on an AMD Ryzen 7 PRO 4750G (8 cores, 16 threads) and 64GB memory, and the greedy method was coded in Python 3.8.10.
4.1.2. Results
Table 2 presents the results obtained by solving randomly generated problems with the ILP-based and the greedy methods. We evaluate the number of drones which is the objective function of the ILP-based method and the algorithm runtime. The purpose of employing the former is to identify the minimum number of drones required to complete the patrolling task, while the latter is utilized to pinpoint areas where the algorithm runtime required to attain the optimal solution increases significantly. This information serves as a critical foundation for selecting the appropriate method for solving real-world problems, especially when taking into consideration the scale of the problem.
As shown in Table 2, the ILP-based method can solve problems with 13 or fewer points within 7 seconds. However, for problems with 14 or more points, the algorithm runtime increases significantly. The greedy method consistently solves problems within 1 second, regardless of problem size. However, the minimum number of drones it finds is often higher compared to the ILP-based method. In this case, the greedy method found solutions with an inferior number of drones in 73.3% of the problems.
Table 2. The comparison of numerical results obtained by solving instances using the ILP-based method and the greedy method.
4.1.3. Discussions
The significant increase in algorithm runtime observed for problems with 14 or more points when utilizing an ILP-based method can be attributed to several factors. These factors include:
• In problems involving 14 or more points, the resulting number of drones is two or three. This is because the problem size is close to the upper bound of what can be patrolled by two drones. Consequently, if two drones are deemed insufficient for patrolling the area, a complete recalculation of the problem is required.
• When the minimum number of drones required is three, the number of candidate optimal routes becomes significantly larger compared to the case where two or fewer drones are required. Consequently, the time required to determine the optimal solution increases.
The observed deterioration in the number of drones required when utilizing the greedy method compared to the ILP-based method can be attributed to several factors, primarily stemming from the inherent differences between the two approaches. These factors include: The ILP-based method considers all possible routes and selects the most efficient one with the minimum number of drones. In contrast, the greedy method prioritizes the shortest route at each step without considering the overall efficiency.
On the other hand, the greedy algorithm is not susceptible to the increased complexity of the overall problem caused by an increasing number of points. This is because the greedy algorithm’s focus on local optimization remains consistent regardless of the problem’s size.
The ILP-based method is well-suited for solving smaller problems due to its efficiency. However, for large-sized problems, the greedy method becomes a preferable choice due to its significantly faster algorithm runtime, even though it may not always find the absolute optimal solution.
4.2. University Campus
4.2.1. Setup
As a realistic building, we assume the Osaka-Ibaraki Campus of Ritsumeikan University (OIC). The OIC is considered to be an important site for demonstration experiments within Ritsumeikan University, which aims to maximize the use of its campus as a place for open innovation. One of the defining characteristics of the OIC is its openness to the community. However, this very openness necessitates continuous patrolling security due to the influx and egress of a large number of unspecified individuals. On the other hand, cost containment is crucial due to the limited number of security guards and budget constraints. Our proposed method can contribute to cost reduction by facilitating efficient patrolling with a minimal number of drones. Figure 2 shows a map of the OIC.
Figure 2. The map of the Osaka-Ibaraki Campus of Ritsumeikan University (OIC) [
29].
We obtained patrol routes for buildings A, B, and C in this paper. Description of buildings A, B, and C are provided below.
• Building A: Classrooms, Research Labs, and Offices
• Building B: Library, Halls, Facilities for Research and Industry-Academia Collaboration
• Building C: Cafeteria, Classrooms, Seminar House
The case study involved creating a graph representation of building A–C. This graph was constructed by placing points at 89 points throughout the buildings. Each point is connected to at least one other point by an edge, resulting in a total of 136 edges. As described in Section 4.1, the greedy method was chosen for this case study due to its suitability for handling large-sized problems compared to the ILP-based method. The maximum flight time for the drone used in this case study is 1200 seconds.
4.2.2. Results
Table 3 summarizes the minimum number of drones required to patrol building A–C, along with the flight time of each drone and the algorithm runtime. As shown in Table 3, four drones are necessary to patrol the A–C buildings of the OIC. In addition, this solution was obtained within five seconds.
Table 3. Performance of the greedy method in the case study.
5. Conclusions
Our paper proposes two methods for facility patrols: an ILP-based method and a greedy method. We compare their performance in terms of the minimum number of drones required and algorithm runtime through experiments. The experiments revealed that the ILP-based method effectively reduces the number of drones needed for patrolling compared to the greedy method. On the other hand, the ILP-based method’s algorithm runtime can significantly increase for problems with more than 14 points. In contrast, the greedy method consistently achieves fast algorithm runtime regardless of problem size. A case study using Ritsumeikan University OIC applied the greedy method to determine the minimum number of drones required for patrolling the facility. The findings of this study can be utilized to implement a flexible approach, where the ILP-based method is employed for problems with less than 13 points, and the greedy method is used for larger problems. This adaptive strategy can be leveraged to find drone patrol routes based on the problem scale. Furthermore, this strategy can help to avoid the need for an excessive number of drones, thereby contributing to the reduction of facility security costs.
Due to its inherent focus on local optimality, the greedy algorithm may produce solutions that deviate significantly from the global optimum. However, the solution generated by the greedy algorithm can serve as a valuable initial solution for a genetic algorithm. Consequently, investigating the implementation of genetic algorithms presents a promising avenue for future research. Additionally, a comparative analysis between the genetic algorithm and other heuristic methods is warranted, as the extensive search space explored by genetic algorithms can lead to increased algorithm runtime.
Furthermore, identifying the optimal depot locations could lead to a more efficient drone patrol route with fewer drones required.
Author Contributions
Conceptualization, K.M. and H.T.; Methodology, K.M., M.N, H.N. and H.T.; Software, K.M.; Investigation, K.M.; Resources, H.T.; Data Curation, K.M.; Writing—Original Draft Preparation, K.M.; Writing—Review & Editing, K.M., M.N, H.N. and H.T; Visualization, K.M.; Supervision, H.T.; Project Administration, K.M.; Funding Acquisition, H.T.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
This work is partly supported by Japan Society for the Promotion of Science (KAKENHI Grant Number 20H04160) and partly commissioned by New Energy and Industrial Technology Development Organization (Project Number JPNP22006).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1.
Kakiuchi R, Tran DT, Lee JH. Evaluation of human behavior detection and interaction with information projection for drone-based night-time security.
Drones 2023,
7, 307.
[Google Scholar]
3.
Yi W, Sutrisna M. Drone Scheduling for Construction Site Surveillance.
Comput.-Aided Civil Infrastruct. Eng. 2021,
36, 3–13.
[Google Scholar]
4.
Kim SJ, Lim GJ. Drone-Aided Border Surveillance with an Electrification Line Battery Charging System.
J. Intell. Robotic Syst. 2018,
92, 657–670.
[Google Scholar]
5.
[Japan’s First Fully] Indoor Demonstration of AI-Powered Fully Autonomous Flying Drone Security System at TOKYO SKYTREE TOWN~Realization of Human Power Saving and Efficiency Improvement in Security Using Drones~ (In Japanese). Available online:
https://www.alsok.co.jp/company/news/news_details.htm?cat=2&id2=1039 (accessed on 7 March 2024).
6.
Dorling K, Heinrichs J, Messier GG, Magierowski S. Vehicle Routing Problems for Drone Delivery.
IEEE Trans. Syst. Man Cybern. Syst. 2016,
47, 70–85.
[Google Scholar]
7.
Campbell JF, Corberán Á, Plana I, Sanchis JM. Drone Arc Routing Problems.
Networks 2018,
72, 543–559.
[Google Scholar]
8.
Corberán Á, Eglese R, Hasle G, Plana I, Sanchis JM. Arc Routing Problems: A Review of the Past, Present, and Future.
Networks 2021,
77, 88–115.
[Google Scholar]
9.
Wu G, Zhao K, Cheng J, Ma M. A Coordinated Vehicle-Drone Arc Routing Approach Based on Improved Adaptive Large Neighborhood Search.
Sensors 2022,
22, 3702.
[Google Scholar]
10.
Mori K, Nishira M, Nishikawa H, Tomiyama H. Surveillance Routing with a Minimum Number of Drones. In Proceedings of the 2023 Eleventh International Symposium on Computing and Networking Workshops (CANDARW), Matsue, Japan, 27–30 November 2023; pp. 366–367.
11.
Mei-Ko K. Graphic Programming Using Odd or Even Points.
Chin. Math. 1962,
1, 237–277.
[Google Scholar]
12.
Calogiuri T, Ghiani G, Guerriero E, Mansini R. A Branch-and-Bound Algorithm for the Time-Dependent Rural Postman Problem.
Comput. Operations Res. 2019,
102, 150–157.
[Google Scholar]
13.
Monroy-Licht M, Amaya CA, Langevin A. Adaptive Large Neighborhood Search Algorithm for the Rural Postman Problem with Time Windows.
Networks 2017,
70, 44–59.
[Google Scholar]
14.
Monroy IM, Amaya CA, Langevin A. The Periodic Capacitated Arc Routing Problem with Irregular Services.
Discret. Appl. Mat. 2013,
161, 691–701.
[Google Scholar]
15.
Benavent E, Corberán Á, Laganà D, Vocaturo F. The Periodic Rural Postman Problem with Irregular Services on Mixed Graphs.
Eur. J. Oper. Res. 2019,
276, 826–839.
[Google Scholar]
16.
Archetti C, Guastaroba G, Speranza MG. An ILP-Refined Tabu Search for the Directed Profitable Rural Postman Problem.
Discret. Appl. Math. 2014,
163, 3–16.
[Google Scholar]
17.
Bianchessi N, Corberán Á, Plana I, Reula M, Sanchis JM. The Profitable Close-Enough Arc Routing Problem.
Comput. Oper. Res. 2022,
140, 105653.
[Google Scholar]
18.
Moazzeni S, Tavana M, Darmian SM. A Dynamic Location-Arc Routing Optimization Model for Electric Waste Collection Vehicles.
J. Clean. Prod. 2022,
364, 132571.
[Google Scholar]
19.
Amini A, Tavakkoli-Moghaddam R, Ebrahimnejad S. A Robust Location-Arc Routing Problem Under Uncertainty: Mathematical Model with Lower and Upper Bounds.
Comput. Appl. Math. 2020,
39, 1–36.
[Google Scholar]
20.
Manyam SG, Casbeer DW, Sundar K. Path Planning for Cooperative Routing of Air-Ground Vehicles. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 4630–4635.
21.
Luo Z, Liu Z, Shi J. A Two-Echelon Cooperated Routing Problem for a Ground Vehicle and Its Carried Unmanned Aerial Vehicle.
Sensors 2017,
17, 1144.
[Google Scholar]
22.
Hu M, Liu W, Lu J, Fu R, Peng K, Ma X, et al. On the Joint Design of Routing and Scheduling for Vehicle-Assisted Multi-UAV Inspection.
Future Gener. Comput. Syst. 2019,
94, 214–223.
[Google Scholar]
23.
Xu B, Zhao K, Luo Q, Wu G, Pedrycz W. A GV-Drone Arc Routing Approach for Urban Traffic Patrol by Coordinating a Ground Vehicle and Multiple Drones.
Swarm Evolut. Comput. 2023,
77, 101246.
[Google Scholar]
24.
Luo H, Zhang P, Wang J, Wang G, Meng F. Traffic Patrolling Routing Problem with Drones in an Urban Road System.
Sensors 2019,
19, 5164.
[Google Scholar]
25.
Munishkin AA, Milutinović D, Casbeer DW. Min-Max Time Efficient Inspection of Ground Vehicles by a UAV Team.
Robot. Auton. Syst. 2020,
125, 103370.
[Google Scholar]
26.
Petitprez E, Georges F, Raballand N, Bertrand S. Deployment Optimization of a Fleet of Drones for Routine Inspection of Networks of Linear Infrastructures. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021.
27.
Bang-Jensen J, Gutin G, Yeo A. When the Greedy Algorithm Fails.
Discret. Optim. 2004,
1, 121–127.
[Google Scholar]
28.
Johnson DS, Gutin G, McGeoch LA, Yeo A, Zhang W, Zverovitch A. Experimental Analysis of Heuristics for the ATSP. In The Traveling Salesman Problem and Its Variations; Springer: Boston, MA, USA, 2007; pp. 445–487.