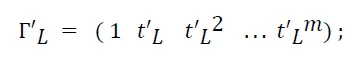Model for Forecasting the Raw Material Base of the Textile Industry Based on the Analysis of the Dynamics of Production Volumes

Nikitina, Lyudmila; Kraikina, Elizabeth; Bogdanov, Alexander

doi:10.70322/ism.2024.10013

Intelligent and Sustainable Manufacturing

Submit to

Article Open Access

Model for Forecasting the Raw Material Base of the Textile Industry Based on the Analysis of the Dynamics of Production Volumes

Lyudmila Nikitina Elizabeth Kraikina Alexander Bogdanov ^*

Author Information

Saint Petersburg State University of Industrial Technologies and Design, Bolshaya Morskaya Street, 18, Saint Petersburg 191186, Russia

Authors to whom correspondence should be addressed.

Views:558

Downloads:87

Intelligent and Sustainable Manufacturing 2024, 1 (2), 10013; https://doi.org/10.70322/ism.2024.10013

Received: 04 May 2024 Accepted: 21 August 2024 Published: 30 August 2024

ABSTRACT: The scientific article analyzes the dynamics of textile industry production in the USSR and the Russian Federation from 1985 to 2022 years.The article provides a fairly complete overview of modern methods of forecasting the development of objects, mainly based on time series analysis, including issues of forecasting cyclic and discontinuous processes, forecasting multidimensional objects with a correlated system of indicators. Authors calculate the forecast until 2026 year based on a bank of mathematical forecasting models implementing various monotonic nonlinear transformations both along the ordinate axis and along the abscissa axis. The criterion of the minimum variance of the forecast error was used as a criterion for selecting a specific model from the bank. The scientific value of the article lies in the fact that, for the first time, it offers a criterion for choosing a mathematical model from a set of them, which uses the minimum estimate of the variance of forecast errors for this model. This work can be considered a step towards the creation of artificial intelligence since the selection of the optimal model for a specific time series allows to obtain a training sample for it, which is fundamentally impossible to obtain without it.

Keywords: Fabric; USSR; Russian Federation; Dynamics analysis; Forecasting; Modeling; Time series

1. Introduction

The products of light industry enterprises are consistently in steady demand from consumers. However, according to official data from the Federal State Statistics Service, the share of light industry in the total industrial production of the Russian Federation is less than 1%. The project titled “Strategies for the Development of Light Industry in Russia up to 2025” has been developed, aimed at stimulating the development of domestic production of competitive goods with high added value, can become one of the factors of the industry’s development. It is expected that the volume of light industry goods shipped will increase from 520.6 billion rubles in 2019 to 631 billion rubles in 2025. Various government support measures have been developed for this purpose. The enterprises of the industry carry out a full cycle of production of goods: from the primary processing of raw materials to the sale of finished products. Therefore, the light industry is a multidisciplinary industry which employs many workers. For the development of the textile and light industry, it is necessary to provide it with a raw material base, which includes the production of flax, cotton and silk. The purpose of this article is to predict the development of the raw material base of the textile and light industry. The article provides a fairly complete overview of modern methods of forecasting the development of objects, mainly based on time series analysis, including forecasting cyclic and discontinuous processes, forecasting multidimensional objects with a correlated system of indicators and creating banks of mathematical forecasting models. Due attention is also paid to forecasting based on deterministic and stochastic mathematical models of ongoing processes. The purpose of the study is a detailed analysis of the production of the raw material base of textile industry enterprises, namely: cotton, linen, silk fabrics for the period 1985–2022 years on the territory of the USSR and the Russian Federation. Before the Soviet Union collapsed, the RSFSR had a well-developed production of cotton, linen, and silk fabrics.The USSR was one of the three most developed countries in the production of textile products. In conditions of technological isolation, global changes are taking place in the textile industry on the territory of the Russian Federation, which requires the development of production factors. At the moment, the textile industry in the Russian Federation largely depends on external supplies of raw materials, which account for about 70% of the total volume [1]. Taking into account the increase in prices for imported raw materials, this leads to a sharp increase in the cost of the final product. The main objective of the study was to build a forecast of the development of the textile industry of the Russian Federation for the next few years. The forecast was carried out based on the analysis of time series of textile industry indicators over the past 20 years using a bank of mathematical forecasting models and a criterion for choosing a model with a minimum variance of forecast error. The scientific value of the article lies in the fact that, for the first time, it offers a criterion for choosing a mathematical model from a certain set of them, which uses the minimum variance of forecast errors for this model. An analytical expression is obtained for estimating the variance of forecast errors based on polynomial models in the presence of nonlinear transformations along both the abscissa and ordinate axes.

2. Materials and Methods

This section gives a classification of forecasting methodsand their essence is briefly described. In particular, methods for predicting discontinuous and cyclic processes andmethods for predicting multidimensional objects with a correlated system of indicators, are considered. Modern forecasting methods can be classified into three main groups [1,2,3]: expert assessment methods; extrapolation methods and mathematical modeling methods; The method of expert assessment is based on using an individual or group opinion on the forecasts of the development of the object [4]. Individual expert assessments are the appeal of experts’ opinions independently of each other. In contrast, group expert assessments are the result of a general discussion of the situation by all members of the group. The most effective methods are questionnaires with feedback, which occupy an intermediate position between individual and group expert assessments.Their advantage is the influence of the opinions of some experts on others by rethinking the initial judgments based on the analysis of the statements of other experts. The extrapolation method consists of spreading trends and connections for a certain period in the future. The method is based on an intuitive idea of some kind of interference-free essence of the analyzed process. The application of this method boils down to constructing the best description of the regular component in some sense f(t) and extrapolating it to a forecast point in time. The author Afanasyev V.N., Yuzbashev M.M.,Chetyrkin E.M. note as functions of f(t), [5,6] are usually used: linear, polynomial, and other simple mathematical dependencies. To obtain a variety of mathematical prediction models based on polynomials, various nonlinear monotonic transformations can be used along the abscissa (time) axis and the ordinate axis for the analyzed time series [7,8,9]. However, the biggest question when applying the extrapolation method is the legality of extending past trends into the future. Over time, both the parameters of the models and the mathematical dependencies themselves may change, and various qualitative changes (jumps) may occur. The development of many objects can be cyclical. For example, business cycles of various frequencies are observed in economic dynamics, including the so-called Kondratiev long waves. The mathematical model of forecasting cyclic processes is considered in [10,11,12,13,14]. The development of the predicted object may represent an alternation of evolutionary and discontinuous stages (jumps). In this case, it can be recommended to use a mathematical model based on the representation of the dynamics of the indicator as the sum of the evolutionary component and abrupt changes [15,16,17]. To account for the possibility of a smooth change in the regular component over time, so-called adaptive models are used, which include exponential smoothing models [18,19] and the Box-Jenkins model [18,20,21,22,23], which is more general with respect to the exponential smoothing model. Mathematical modeling methods involve the development of a deterministic or stochastic model. The construction of a deterministic model is based on the conclusion of the mathematical dependence of the studied indicator on the main determining factors that are not random. Stochastic models take into account the probabilistic nature of changes in indicators and, unlike deterministic models, present the forecast result as a set of probabilities of different values of the indicator or the density of the probability distribution. The theoretical foundations of the mathematical modeling method are described in [24,25,26]. Mathematical modeling methods are widely used in predicting the development of infectious diseases in both human and animal populations, as well as in economics and marketing. General approaches to constructing models of the mathematical theory of epidemics (MTE) are considered in [27,28,29,30,31]. Deterministic models for a closed population include the Kermak and McKendrick model [32,33,34], the Weiss model (with vectors) [35], as well as a model developed with the participation of the author [36]. Stochastic models include a simple stochastic model [37,38], a general stochastic model [39,40,41], the Downton model [42], a stochastic version of the Weiss model [43], and an extended simple stochastic model [44,45]. The general principles of mathematical modeling of the epizootic process are considered in [46,47,48]. Models of the spatial spread of epidemics are considered in [27,28], and epizootics—in [49,50,51,52], simulation models—in [53,54,55,56,57,58]. The principle of developing and synthesizing MTE models for specific diseases is discussed in [56,57,58,59], and recommendations on using deterministic or stochastic models are presented in [60,61,62]. Mathematical models have been successfully used to predict leptospirosis [63], influenza [64,65], tuberculosis [66,67] and especially COVID-19 [68,69,70,71,72,73]. Mathematical forecasting models in economics and marketing include [74,75,76]. It should be noted that there are also a number of specific forecasting methods: the method of envelope curves (used to predict the development of technology taking into account the change of generations), “engineering forecasting” (based on the analysis of patent information) [77,78,79,80], the predictive graph method (predicting the probability or time of occurrence of events) [81] and others [82,83,84,85,86]. The variety of forecasting methods and models is because they focus on a certain class of objects and prevailing conditions. Therefore, when choosing a forecasting method and constructing a mathematical forecasting model, one should take into account the nature of the forecasting object (scientific, technical, economic, social, natural), its dimension, complexity (the degree of interrelation between elements), the nature of development (the presence of cycles, jumps, etc.), the degree of determinism, as well as available information sources. Modern forecasting, tends to create hybrid models consisting of several separate forecasting models in which the forecast is formed as a weighted sum of forecasts obtained using various methods and models [85,86,87,88,89]. Let’s consider the case when the forecasting object is characterized by a certain set of indicators—$$\{P_{1},P_{2},\ldots,P_{n}\}$$. It is possible that there may be fairly close correlations between individual indicators. This circumstance can be used to reduce the dimension of the forecasting problem, which assumes: based on the analysis of the correlation matrix of n indicators, the allocation of k variables (k < n), the variation of which, with a sufficient degree of adequacy, allows us to explain the variation in the values of the initial indicators; -$$\,$$building models of the relationship of baseline indicators with selected variables; -$$\,$$prediction of the values of the selected variables at a given time t_L; -$$\,$$determination of the forecast values of the initial indicators based on communication models and the forecast values of the selected variables. The advantage of this approach is that the selected variables are usually poorly correlated. This makes it possible to predict them independently and avoid using complex econometric models of interrelated series, which is very problematic in conditions of limited statistical information and many parameters of such models. In addition, as a result of this approach, the task of linking forecasts of individual indicators is automatically solved. One of the approaches to the problem of dimension reduction is the use of factor analysis (FA) apparatus [90,91,92,93,94]. The main hypothesis of the FA is that the totality of correlated indicators can be described using a small number of directly unobservable hypothetical quantities—common factors (OF). The FA model has the form:

```latexP_{j}=\sum_{r=1}^{k}a_{jr}f_{r}+d_{j}u_{j},\quad(j=1,...,n)```

(1)

where: f_r—is the value of the rth OF; a_jr—is the factorial load of the r-th OF on the j-th indicator; u_j—is the value of the j-th characteristic factor; d_j—is the load of the j-th characteristic factor; k—is the number of OF. At the same time, k < n. Forecasting of the OF by time series does not differ in any way from forecasting the initial indicators. However, the dynamics of the OF, as a rule, is characterized by greater stability. When predicting indicators for OF, no special construction of communication models is required since the factor model acts as such a model. However, using the FA apparatus is possible only when using the extrapolation method of forecasting OF, since experts cannot predict the development of hypothetical OF, which does not have a clear economic meaning. Therefore, when using the expert method of forecasting indicators of the market situation, it is advisable to use other methods of reducing the dimension—the allocation of the so-called “leading” indicators [93,94,95,96]. The reduction in the dimension of the forecasting task is carried out by dividing the entire set of indicators G into two groups: “leading”—G₁ (independently predicted) and “driven”—G₂ (predicted based on models of communication with “leading” indicators. A natural condition for assigning an indicator to the “slave” group is the sufficient closeness of its statistical relationship with the G₁ group, which should ensure acceptable accuracy of its forecast. So, if the indicator P_i is closely related to the indicator $$P_j(r(P_i,P_j)\approx1)$$, then it is enough to include one of them in the “leading” group. It is also obvious that if the P_i indicator does not have a significant statistical relationship with any of the other indicators. It should be attributed to the “leading” group. In general, the issue of dividing indicators into groups G₁ and G₂ is quite complicated. When solving this problem, the goal is to ensure a minimum number of indicators in the G₁ group with a given closeness of the correlation between the “slave” indicators and the “leading” ones. The last condition applies to each of the “slave” indicators and acts as the following restriction:

```latex\min R(P_i,G_1)\geq R_0,P_i\in G_2```

where: R(P_i,G₁ )—the coefficient of multiple correlation of the “slave” indicator P_i with the group G₁; R₀—the minimum allowable multiple correlation coefficient. The stated task is optimizing the composition of the group of “leading” indicators in the presence of restrictions. Its solution is considered in the author’s works [95,96,97,98]. The effectiveness of dimensionality reduction methods has been studied in [99,100,101]. The issue of estimating the accuracy and reliability of forecasts is considered in [102,103], and the stability of the obtained models of the relationship between variables in [104,105,106].

3. Mathematical Model of Forecasting

This section discusses a mathematical forecasting model based on selecting polynomial models for time series obtained using nonlinear monotonic transformations along both the abscissa and ordinate axes. The criterion for choosing a model is the one with the lowest forecast variance, which is determined using an analytical expression.. In addition, when selecting a model, its adequacy is assessed according to the Darbin criterion. Watson and the cumulative criterion of consent. Let’s consider the issue of creating a bank of various mathematical forecasting models anddeveloping procedures for automated selection of the «best» time series model in some sense. When creating a bank of mathematical forecasting models, polynomial models of the form can be used as a basis.

```latexy'(t')=a_0+a_1t'+a_2(t')^2+\cdots a_m(t')^m+\varepsilon_{t'}'```

(2)

where: m—is the order of the polynomial; α_j—is the jth parameter of the model; $$\varepsilon_{t'}^{\prime}$$—is an uncorrelated random variable with zero mathematical expectation and variance σ². The parameters of polynomial models, due to their linearity with respect to the α_j parameters, are estimated using the least squares method, which leads to the following expression for calculating parameter estimates [107]:

```latex\hat{a}=(\Gamma'\Gamma)^{-1}\Gamma'Y,```

(3)

```latex\Gamma=\begin{pmatrix}1&t_1'&...&&(t_1')^m\\1&t_2'&...&&(t_2')^m\\...&...&&...&...\\1&t_n'&&...&(t_n')^m\end{pmatrix};Y=\begin{pmatrix}y_1'\\y_2'\\...\\y_n'\end{pmatrix};```

where: n—the number of points in the time series under consideration; $$t_{j}^{\prime}$$—the moment of time corresponding to the jth point of the time series; $$y_j^{\prime}$$—the value of the indicator in question at a time $$t_{j}^{\prime}$$. In this case, the variance of the forecast error of the indicator $$y^{\prime}$$ at time $$t_L^{\prime}$$ can be estimated based on the following analytical expression [108]:

```latex\widehat{D}\{y'(t_{L}')-\hat{y}'(t_{L}')\}=\hat{\sigma}^{2}\{1+\Gamma_{L}'(\Gamma'\Gamma)^{-1}\Gamma_{L}\},```

(4)

where:

```latex\hat{\sigma}^2=\sum_{j=1}^n(y_j'-\hat{y}_j')^2/(n-m-1),```

$$\hat{y}_j^{\prime}$$—the forecast of the $$y_j^{\prime}$$ indicator based on the trend model. To obtain a variety of mathematical prediction models based on polynomials, we will use various nonlinear monotonic transformations both along the abscissa (time) axis and along the ordinate axis for the analyzed time series [7,8,9]. The class of nonlinear transformations we use along the abscissa (time) axis $$t^{\prime}=f_1(t)$$ includes:

```latex(a)\,t' = t;\quad(b)\,t' = 1/t;\quad(c)\,t'=lnt;\quad(d)\,t' = \sqrt[k]{t}.```

The class of transformations along the ordinate axis $$y^{\prime}=f_2(y)$$ contains:

```latex(a)\,y^{\prime}=y;(b)\,y^{\prime}=1/y;\quad(c)\,y^{\prime}=y^{k};\quad(d)\,y^{\prime}=lny;\quad(e)\,y^{\prime}=e^{y};\quad(f)\,y^{\prime}=e^{-y}.```

The set of mathematical forecasting models obtained using a 3rd-order polynomial approximation of the transformed time series is shown in Table 1.

Table 1. Mathematical forecasting models for к = 2

The advantage of the proposed approach is that, despite the nonlinearity of the mathematical models obtained relative to the estimated parameters, it is possible to apply OLS to the transformed time series since a polynomial model is selected for it. At the same time, the range of mathematical dependencies in Table 1 is quite wide. Another important issue when creating a bank of forecasting models is the issue of choosing a model. It seems logical to use the minimum variance of the forecast error as the criterion for selecting a mathematical forecasting model. When there are no nonlinear transformations along the ordinate axis, the variance of the forecast error can be calculated using the following Formula (3). The estimate of the variance of the forecast error in the presence of nonlinear transformations along the ordinate axis is calculated using the following formula [7,8,9]:

```latex\widehat{D}\{y(t_L)-\hat{y}(t_L)\}=(\frac{\partial f_2^{-1}(y^{\prime})}{\partial y^{\prime}})^2|y^{\prime}=\hat{y}^{\prime}(t_L^{\prime})\hat{\sigma}^2(1+\Gamma_L^{\prime}(\Gamma^{\prime}\Gamma)^{-1}\Gamma_L),```

(5)

Note that the last expression is obtained under the assumption that random variables are uncorrelated ε_t. This condition is a well-known criterion for the adequacy of models and must be verified. Diagnostic verification of the adequacy of models is reduced to testing the statistical hypothesis of the uncorrelation of random variables ε_t. The Durbin-Watson and cumulative consent criteria can be used for this purpose [7]. The criterion for choosing a mathematical model is the minimum variance of the prediction error of the initial time series from a set of transformations that have been tested for the adequacy of the model according to both tests. Note that to improve the accuracy of the forecast, you can try to simplify the models, excluding statistically insignificant parameters from them. The hypothesis that the true value of the j-th parameter of the model is zero is rejected if the following condition is met [108]:

```latex/\hat{a}_j/>t_\alpha\quad\sqrt{\hat{D}(\hat{a}_j)},```

where: t_α—tabular value of the Student’s criterion of significance level for $$v=n-m-1$$ degrees of freedom. Otherwise, parameter $$\hat{a}_{J}$$ should be considered statistically insignificant. Thus, for each of the possible variants of nonlinear transformations (types of model): – Transformation of the time points $$t^{\prime}=f_1(t)$$ and the predicted indicator $$y^{\prime}=f_{2}(y)$$ in accordance with Table 1; – Estimation of the parameters of the polynomial model according to Formula (2); – Obtaining the predicted values of the transformed indicator $$\hat{y^{\prime}}(t_{L}^{\prime})$$ according to the polynomial model; – Finding the predicted value of the initial indicator using the inverse transformation $$\hat{y}(t_{L})=f_{2}^{-1}\left(\hat{y^{\prime}}(t_{L}^{\prime})\right)$$; – Estimation of the variance of the prediction error of the initial time series according to Formula (4); – Diagnostic verification of the adequacy of the model. From various adequate models, an option is selected that provides a minimum variance of the forecast error. It is also possible for experts to participate in the preliminary selection of a subset of tested models [9]. The choice of the polynomial order is carried out by sequentially iterating 1,2,...k until a model with a minimum variance of the forecast error is obtained. The value of k is limited by the fact that as the order of the polynomial increases, the number of estimated parameters increases. With a small amount of experimental data, the estimates of these parameters may become statistically unreliable according to the Student’s criterion. As part of the study, the polynomial order was viewed in the range from 1 to 3.

4. Initial Data and Calculation Results

This section examines the forecasted objects, specifically the time series of silk, cotton and wool production from 1985 to 2022 years. A meaningful analysis of the dynamics of these indicators has been carried out. The periods that can be used for forecasting the volume of production of these raw materials for the period up to 2026 year have been identified. The dynamics of silk fabric production in the USSR and the Russian Federation for the period 1985–2022 years are shown in Figure 1.

Figure 1. Production of silk fabrics on the territory of the USSR-the Russian Federation in 1985–2022 years (million m2) [109,110].

As can be seen from Figure 1, since 1990 year, there has been a significant decrease in the production of silk fabrics. In Soviet times, the cotton industry was the leading light industry. It consisted of more than 240 enterprises and production associations in the USSR. The most important principle of the placement of Soviet industrial enterprises was to approach the sources of raw materials and areas of consumption of products. With the collapse of the USSR in 1991 year, great difficulties arose with the raw material base. Due to the fact that cotton was the main raw material for textile products and Uzbekistan became an independent state as the main supplier of cotton, Russia needed to replace cotton [111]. As can be seen from Figure 2, in 1988 year, the production of cotton fabrics reached a maximum and amounted to 8106 million m². Since 1998 year , there has been an overall increase in production, and in 2006 year this figure amounted to 2222 million m², which is 1142 million m² more than in 1998 year. In 2021 year, the volume of production of cotton fabrics reached its maximum value and amounted to 899 million m².

Figure 2. Production of cotton fabrics on the territory of the USSR-the Russian Federation in 1985–2022 years (million m2) [109,110].

As can be seen from Figure 3, in the period 1985–1989 years, there was a slight increase in the production of woolen fabrics, reaching the level of 721 million m², and after the collapse of the USSR, this figure fell sharply to the level of 276 million m², that is almost 2.5 times.

Figure 3. Production of wool fabrics on the territory of the USSR-the Russian Federation in 1985–2022 years (million m2) [109,110].

As a result of testing the models listed in Table 1 for the dynamics of silk production, model 4 was in the first place according to the criterion of the minimum variance of the forecast error when using 3rd-order polymers. For this model, the significance of parameter estimates according to the Student’s criterion was verified. Estimates of the parameters of model 4, their standard deviations and the values of the Student’s criterion are given in Table 2.

Table 2. Estimation of model parameters 4.

The tabular value of the Student’s criterion of the significance level α = 0.10 at 23 degrees of freedom is 1.71. Thus, parameter a₁ turned out to be statistically insignificant and the variable t should be excluded from the model. The recalculation allowed us to obtain the following parameter estimates (Table 3).

Table 3. Estimates of the parameters of the adjusted model.

All parameters of the new model are statistically significant at the significance level α = 0.05 (the tabular value of the Student’s criterion is 2.06) and it can be used for forecasting. The obtained forecasts for 2023–2026 years and estimates of their variances are shown in Table 4.

Table 4. Forecasts of silk production (million m²) for 2023–2026 years.

Since the coefficients of variation are less than 0.25, the forecasts obtained can be considered acceptable. Once again, we recall that they are the most accurate among the forecasts obtained using other models in Table 1. As a result of testing the models listed in Table 1 for the dynamics of cotton production, model 2 turned out to be in first place according to the criterion of minimum variance of the forecast error when using a 2nd-order polynomial. Estimates of the parameters of model 2, their standard deviations and the values of the Student’s criterion are given in Table 5.

Table 5. Estimation of model parameters 2 for cotton.

All model parameters are statistically significant at the significance level α = 0.05 (the tabular value of the Student’s criterion is 2.06) and it can be used for forecasting. The obtained forecasts for 2023–2026 years and estimates of their variances are shown in Table 6.

Table 6. Forecasts of cotton production (million m²) for 2023–2026 years.

As a result of testing models for the dynamics of wool production, model 2 also appeared in the first place according to the criterion of the minimum variance of the forecast error when using the 2nd order polynomial. The estimates of the model parameters, their standard deviations and the values of the Student’s criterion are given in Table 7.

Table 7. Estimation of model parameters 2 for wool.

All parameters of the model are statistically significant at the significance level α = 0.05. The obtained forecasts for 2023–2026 years and estimates of their variances are shown in Table 8.

Table 8. Forecasts of wool production (million m²) for 2023–2026 years.

5. Conclusions

The use of a bank of mathematical forecasting models based on time series analysis with a criterion for choosing a model with the lowest variance of forecast error allows us to obtain the most accurate forecast, which will affect the quality of management of the development of the textile industry of the Russian Federation and will contribute to improving the efficiency of using material and organizational resources and, ultimately, increasing labor productivity and profits of enterprises. The scientific value of the article consists in substantiating the criterion for choosing a mathematical model, which will allow in each specific practical situation to choose a model with a minimum variance of forecast error. This approach has significant scientific novelty in comparison with the traditional methodology of choosing a model based on the criterion of the maximum coefficient of determination. It is known from practice that the traditional criterion of the maximum coefficient of determination does not lead to constructing a model with good predictive properties. This work can be considered a step towards the creation of artificial intelligence [112,113,114,115,116,117], since selecting the optimal model for specific time series allows, to obtain a training sample for it, which is fundamentally impossible to obtain without it.

Author Contributions

Analysis of the data under study, L.N. and E.K.; Mathematical forecasting A.B.; validation, writing—review and editing, E.K. and A.B. All authors have read and agreed to the published version of the manuscript.

Ethics Statement

Not applicable.

Informed Consent Statement

Funding

This research received no external funding.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Bogdanov AI. Mathematical Models of Forecasting (Monograph); SPGUTD: St. Petersburg, Russia, 2007; p. 128.

Bestuzhev-Lada IV (Ed.). Forecasting Workbook; MYSL: Fraser, MI, USA, 1982; p. 430.

Theory of Forecasting and Decision-Making: Textbook; Sarkisyan SA, Ed.; Higher School: Moscow, Russia,1977; p. 351.

Glushkov VM. On forecasting based on expert assessments. In Naukovedenie: Forecasting: Informatics; Naukova Dumka: Kiev, Ukraine, 1970; pp. 201–204.

Afanasyev VN, Yuzbashev MM. Time Series Analysis and Forecasting: Textbook; Finance and Statistics: Moscow, Russia, 2012; p. 320.

Chetyrkin EM. Statistical Methods of Forecasting; M-Statistics: Moscow, Russia, 1975; p. 184.

Bogdanov AI, Tulchin LG. Development of a bank and procedures for automated selection of mathematical models for forecasting the technical level of devices. Publication in Sb. Nauch. tr. VNIIEP “Automation of Scientific Research, Design Work and Management in Electrical Engineering”; Saint-Petersburg, Russia; 1990; pp. 58–65.

Bogdanov AI. Expert system for forecasting product quality. In Combinatorial-Statistical Methods of Information Analysis and Processing, Expert Assessment: Thesis. Dokl. III Vsesoyuz. Seminar Schools on September 10–15; Bogdanov AI, Tulchin LG, Eds.; OPI: Odessa, Ukraine, 1990; p. 157.

Bogdanov AI, Orekhov DV. On the Issue of Building an Automated Process Forecasting System Based on Time Series Analysis; Series 1: Natural and Technical Sciences; Bulletin of the St. Petersburg State University of Technology and Design: Saint Petersburg, Russia, 2017; pp. 13–19.

10.

Mostovoy PP, Tormozova NM. The Study of Cyclicity and Forecasting the Dynamics of the Epidemic Process of Various Types of Dysentery; ZHMEI: Tianjin, China, 1979; pp. 21–25.

11.

Ranchov GK. Quantitative Studies of Cyclic Fluctuations in the Epidemiological Process of a Number of Infectious Diseases in Bulgaria; ZHMEI: Tianjin, China, 1989; pp. 59–62.

12.

Shkilna, VA. Sabashkin. Mathematical Modeling and Forecasting of the Epizootic Process of Bovine Tuberculosis. In the Diagnosis of Infectious Animal Diseases: Collection of Scientific Papers; SO RASKHN; IEVS and DV: Novosibirsk, Russia, 1993; pp. 24–28.

13.

Bogdanov AI. Forecasting the parameters of business cycles of market activity. In Problems of Managing the Development of Socio-Economic Systems: Collection of Scientific tr.; Bogdanov AI, Chabrovsky VA, Eds.; SPbGUKiT: St. Petersburg, Russia, 1998; pp. 65–68.

14.

Bogdanov AI. On one mathematical model of forecasting cyclic processes. Math. Model. 2004, 16, 47–54. [Google Scholar]

15.

Reimerov LI. The problem of forecasting leaps in the development of technical means. In Problems of the Development of the Theory of Prognostics and Forecasting Practice: Materials of a Short-Term Seminar [3–4 April 1980]; LDNTP: Saint-Petersburg, Russia, 1980; pp. 20–23.

16.

Bogdanov AI. Development and Research of an Expert Statistical Method for Forecasting the Technical Level of Electrical Measuring Equipment. Publication in Collection of Scientific Papers of VNIIEP “Management of the Sub-Sector and Technical and Economic Research in Electrical Engineering”; St. Petersburg, Russia, 1983; pp. 88–95.

17.

Bogdanov AI. A model for forecasting the abrupt development of technology. In Forecasting Scientific, Technical and Economic Development of the Main Links of the National Economy: Materials of Scientific and Practical Conference on April 17–18; Bogdanov AI, Tulchin LG, Eds.; LDNTP: Russia, St. Petersburg 1990; pp. 72–74.

18.

Lukashin YP. Adaptive Methods of Short-Term Forecasting of Time Series: Textbook; Finance and Statistics: Moscow, Russia, 2003; p. 413.

19.

Svetunkov SG, Svetunkov IS. Methods of Socio-Economic Forecasting: Textbook for Universities; SPbGUEF: St. Petersburg, Russia, 2010; p. 103.

20.

Bogachev VV, Rodionova GA. Generalized linear forecasting model of a one-dimensional time series. In Thesis. dokl. IY Siberian Scientific and Practical Conference on the Reliability of Scientific and Technical Forecasts; GPNTB SB of the USSR Academy of Sciences: Novosibirsk, Russia, 1987; p. 147.

21.

Box J, Jenkins G. Time Series Analysis: Forecast and Management; Levshina AL, Translator; Pisarenko VF, Ed.; Mir: Grodno, Belarus,1974; Issue 1, 406p.

22.

Gorelik IA, Frenkel AA. The experience of using the generalized Box-Jenkins model for forecasting economic indicators. Econ. Math. Methods 1975, 11, 784–789. [Google Scholar]

23.

Koneva ES. The choice of models for real time series: An overview. Autom. Telemech. 1988, 49, 3–18. [Google Scholar]

24.

Buslenko NP. Modeling of Complex Systems, 2nd ed.; Nauka GL, Ed., 1978; p. 400.

25.

Berezhnaya EV (Ed.). Mathematical Methods of Modeling Economic Systems: A Textbook; Finance and Statistics: Moscow, Russia, 2003; p. 110.

26.

Samarsky AA. Mathematical Modeling: Ideas. Methods. Examples; Samarsky AA, Mikhailov AP, Eds.; Fizmatgiz: Nauka, Russia, 1997; p. 320.

27.

Baroyan OV, Rvachev LA, Ivannikov YG. Modeling and Forecasting of Influenza Epidemics for the Territory of the USSR. In Medicine; Academy of Medical Sciences of the USSR: Moscow, Russia, 1977; p. 546.

28.

Rvachev LA. Modeling of influenza epidemics in large territories. In Proceedings of the Management of Health Care Systems: Abstracts of Reports of the International Meeting, 1–3 December 1982, Moscow, Russia, pp. 62–63.

29.

Khodjaev S, Ikramova H, Balogeev T. On forecasting the epidemic process. Publication in Izv. of the Academy of Sciences of the Uzbek SSR; Series of Technical Sciences; Uzbekistan, Tashkent. 1973; pp. 77–78.

30.

Khodjaev SK, Kadyrov KK, Ikramova KZ. On mathematical modeling of the epidemic process. Publication in Izv. of the Academy of Sciences of the Uzbek SSR; Series of Technical Sciences; Uzbekistan,Tashkent,1970; pp. 62–63.

31.

Bailey NTJ. The Mathematical Theory of Epidemics; Griffin: London, UK, 1957; p. 194.

32.

Kermack WO, Mc Kendrick AG. Contributions to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]

33.

Hethcote Herbert W. Asymptotic behavior in a deterministic epidemic model. Bull. Math. Biol. 1973, 35, 607–614. [Google Scholar]

34.

Deakin Michael AB. A standard form for Kermack Mc Kendrick epidemic equations. Bull. Math. Biol. 1975, 37, 91–95. [Google Scholar]

35.

Weiss George H. On the spread of epidemics by carriers. Biometrika 1965, 21, 481–490. [Google Scholar]

36.

Bogdanov AI, Brook MM, Pogrebnyak LL. Development of a deterministic model of the development of the epizootic process for a homogeneous bird population. In Abstracts of the XIX Conference of Young Scientists and Postgraduates on Poultry Farming, 16–18 June 1976; VNITIP: Zagorsk, Russia, 1976; pp. 68–69.

37.

Bailey NTJ. The simple stochastic epidemic: A complete solution in term of known functions. Biometrika 1963, 50, 235–240. [Google Scholar]

38.

Mc Neil Donald R. On the simple stochastic epidemic. Biometrika 1972, 59, 494–497. [Google Scholar]

39.

Bailey NTJ. The estimation of parameters from population data on the general stochastic epidemic. Theor. Popul. Biol. 1971, 2, 253–270. [Google Scholar]

40.

Bailey NTJ. The Mathematical Theory of Infectious Diseases and Its Applications, 2nd ed.; Griffin: London, UK, 1975; p. 413.

41.

Bailey Norman TJ. Current trends in the modelling of infectious disease. In Proceedings of the 8th International Biometric Conference, Constanta, Romania, 25–30 August 1974; Acad. RSR: Bucuresti, Romania, 1975; pp. 113–121.

42.

Denton Gillian M. On Downton’s carrier-borne epidemic. Biometrika 1972, 59, 455–461. [Google Scholar]

43.

Dietz K. On the model of Weiss for the spread of epidemics by carriers. J. Appl. Probab. 1966, 3, 375–382. [Google Scholar]

44.

Kryscio Richard J. On the extended simple stochastic epidemic model. Biometrika 1974, 61, 200–202. [Google Scholar]

45.

Weiss George H, Dishon M. Asymptotic behavior of a generalization of Bailey’s simple epidemic. Adv. Appl. Probab. 1971, 3, 220–221. [Google Scholar]

46.

Bakulov IA. Some research results on the problem of epizootological forecasting (in veterinary practice). Proc. RES 1982, 55, 11–15. [Google Scholar]

47.

Tarshis MG, Konstantinov VM. Mathematical Models of the Epizootic Process; VNIITEISH: Moscow, Russia, 1979; p. 56.

48.

Tarshis MG, Konstantinov VM, Bogomolova MG. Mathematical models in epizootology. Bull. Agric. Sci. 1987, 7, 114–120. [Google Scholar]

49.

Bogdanov AI. Assessment of the risk of disease in poultry farming. In Improvement of Methods for the Prevention of Bird Diseases: Materials of the Scientific and Practical Conference; GNU IEVSiDV SB RASKHN: Novosibirsk, Russia, 2001; pp. 102–108.

50.

Bogdanov AI. Mathematical model of forecasting damage from epizootics. In Poultry Farming: Proceedings of the III Ukrainian Conference on Poultry Farming with International Participation; Institute of Poultry Farming, UAAN: Borki, Poland, 2001; pp. 509–513.

51.

Bogdanov AI, Borisenkova AN. Mathematical model of operational forecasting of the epizootic process at the level of poultry farming. In Poultry Farming: Proceedings of the III Ukrainian Conference on Poultry Farming with International Participation; Institute of Poultry Breeding of UAAN: Borki, Poland, 2001; pp. 506–509.

52.

Bogdanov AI, Nikolaev SV, Panfilov AV. Mathematical model of forecasting the epizootic process at the regional level. In Collection of Scientific Papers “Veterinary Prevention in Industrial Poultry Farming”; Lomonosov: VNIVIP: St. Petersburg, Russia, 1996; pp. 56–61.

53.

Bogomolova MG, Konstantinov VM, Tarshis MG. Simulation Model of the Epizootic Process in a Closed Population. Vet. Med. 1989, 4, 40–43. [Google Scholar]

54.

Konstantinov VM, Bogomolova MG, Tarshis MG. Simulation models of the spread of infection in confined animal populations. Bull. Agric. Sci. 1989, 3, 77–84. [Google Scholar]

55.

Kudryavtsev FS, Brook MM. On the application of simulation methods for modeling epizootics. Publication in Scientific Foundations of Veterinary and Preventive Measures in Industrial Poultry Farming; Chisinau, Moldova, 1977; pp. 199–200.

56.

Bogdanov AI, Borisenkova AN, Korovin RN, Pridybailo ND. Methodology of synthesis of mathematical models for forecasting the epizootic process. Rep. RASKHN 2003, 3, 39–41. [Google Scholar]

57.

Bogdanov AI, Borisenkova AP, Korovin RP, Pridybailo ND. Development of mathematical models for forecasting the epizootic process. Vet. Med. 2003, 10, 25. [Google Scholar]

58.

Aronov VM, Bogdanov AI, Kuzmin VA. Selection of optimal mathematical models for forecasting epizootic processes. Vet. Med. 2012, 7, 18–22. [Google Scholar]

59.

Bogdanov AI, Kuzmin VA, Kudryavtseva AV, Tumansky AY, Prosvirnin GS, Kan FL. The experience of using mathematical models in the epizootological forecasting system. Issues Regul. Regul. Vet. Med. 2015, 3, 67–69. [Google Scholar]

60.

Bogdanov AI, Mongush BS, Kuzmin VA, Orekhov DA, Ravilov RH, Gulyukin AM, et al. Method of selection and synthesis of mathematical models of the epizootic process. Regul. Leg. Regul. Vet. Med. 2022, 4, 46–49. [Google Scholar]

61.

Bogdanov AI, Khakhaev IA, Kuzmin VA, Tsyganov AV, Ponomarenko NP. Analysis of modern approaches to forecasting the epizootic process using mathematical models. Hippology Vet. Med. 2018, 3, 32–39. [Google Scholar]

62.

Bogdanov AI, Mongush BS, Kuzmin VA, Orekhov DA, Nikitin GS, Baryshev AN, et al. Analysis of models of the mathematical theory of epidemics and recommendations for the use of deterministic and stochastic models. Regul. Leg. Regul. Vet. Med. 2022, 4, 37–41. [Google Scholar]

63.

Bogdanov AI, Kuzmin VA, Fogel LS, Kudryavtseva AV, Savenkov KS. Development of a mathematical model for the manifestation of serological reactions in cattle leptospirosis in the Leningrad region. Issues Regul. Regul. Vet.Med. 2015, 1, 46–49. [Google Scholar]

64.

Sebastiani P, Mandl KD, Szolovits P, Kohane IS, Ramoni MF. A Bayesian dynamic model for influenza surveillance. Stat. Med. 2006, 25, 1803–1816. [Google Scholar]

65.

Gass JD, Jr., Kellogg HK, Hill NJ, Puryear WB, Nutter FB, Runstadler JA. Epidemiology and Ecology of Influenza A Viruses among Wildlife in the Arctic. Viruses 2022, 14, 1531. [Google Scholar]

66.

Avilov KK, Romaniukha AA. Mathematical models of the spread and control of tuberculosis. Math. Biol. Bioinform. 2007, 2, 188–318. [Google Scholar]

67.

Pertsev NV, Leonenko VN. Stochastic individual-based model of spread of tuberculosis. Russ. J. Numer. Anal. Math. Model. 2009, 24, 341–360. [Google Scholar]

68.

Gavrilov DV, Abramov RV, Kirilkina АV, Ivshin АА, Novitskiy RE. COVID-19 pandemic prediction model based on machine learning in selected regions of the Russian Federation. FARMAKOEKONOMIKA. Mod. Pharmacoecon. Pharmacoepidemiol. 2021, 14, 342–356. [Google Scholar]

69.

Jain A, Singh RC, Khokher R, Kumar R. Forecasting of COVID-19 Cases Using SARIMA Model in India. Solid State Technol. 2020, 63, 3516–3528. [Google Scholar]

70.

Margenov S, Popivanov N, Ugrinova I, Harizanov S, Hristov T. Mathematical and computer modeling of COVID-19 transmission dynamics in Bulgaria by time-depended inverse SEIR model. AIP Conf. Proc. 2021, 2333, 090024. [Google Scholar]

71.

Wang P, Zheng X, Li J, Zhu B. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics. Chaos Solitons Fractals 2020, 139, 110058. [Google Scholar]

72.

Koltsova EM, Kurkina ES, Vasetsky AM. Mathematical modeling of the spread of COVID-19 in Moscow. Comput. Nanotechnol. 2020, 7, 99–105. [Google Scholar]

73.

Krivorotko OI, Kabanikhin SI, Zyatkov NY, Prikhodko A, Prokhorkin N, Shishlenin MA. Mathematical modeling and forecasting of COVID-19 in Moscow and the Novosibirsk region. Sib. J. Comput. Math. 2020, 23, 395–414. [Google Scholar]

74.

Zhizhelev AV, Zhizhelev AA. Modeling the fame of a candidate in an election campaign. In Information Technologies in Modeling and Management: Proceedings of the Second International Scientific and Practical Conference; Publishing House of SPSTU: St. Petersburg, Russia, 2000; pp. 145–147.

75.

Bogdanov AI, Nikitina LN, Puchkova SV. Model the effects of advertising on consumer behavior. Marketing 2005, 4, 84–91. [Google Scholar]

76.

Bogdanov AI, Nikitina LN, Shchadilova AV. An imitation model of the product life cycle for choosing an assortment strategy. Marketing 2006, 2, 56–62. [Google Scholar]

77.

Alexandrov LV, Karpova NN. Methods of Forecasting Technical Solutions Using Patent Information; VNIIPI: Saint-Petersburg,Russia: 1991; p. 155.

78.

Bogdanov AI, Tulchin LG, Gmoshinsky VG. Model of engineering forecasting of the technical level of devices with limited statistical information. Devices Control. Syst. 1991, 1, 39–40. [Google Scholar]

79.

Gmoshinsky VG, Fliorent GI. Theoretical Foundations of Engineering Forecasting; Nauka GL, Ed.; phys.-mat. Lit: Moscow, Russia: 1973; p. 304.

80.

Timofeeva NM, Meshcheryakov VI, Zagorodnikova IA. System Analysis of Patent Statistics in Forecasting Trends in the Development of Switching Equipment: Methodological Recommendations; VNIIPI: Saint-Petersburg, Russia, 1991; p. 53.

81.

Lopukhin MI. Pattern a Method of Planning and Forecasting Scientific Papers; Soviet Radio: Moscow, Russia, 1971; p. 159.

82.

Danilova DL,.Zhiglyavsky AA.The Main Components of Time Series: the “Caterpillar” Method; Danilov DL, Zhiglyavsky AA, Eds.; St. Petersburg State University: St. Petersburg, Russia, 1997; p. 308.

83.

Golyandina NE. The Caterpillar-SSA Method: Time Series Forecast: Textbook; St. Petersburg State University: St. Petersburg, Russia, 2004; p. 49.

84.

Belyakov AG. Forecasting Time Series Based on the Method of Analogues; Belyakov AG, Mandel AS, Eds.; IPU: Geneva, Switzerland, 2002; p. 59.

85.

Sidelnikov YV. Theory and Organization of Expert Forecasting; IMEMO: Moscow, Russia, 1990; p.195.

86.

Bogdanov AI. Mathematical model of forecasting of discontinuous processes. In Bulletin of SPGUTD; No.1. Series 1. Natural and Technical Sciences: St. Petersburg, Russia, 2011; pp.57–62.

87.

Vasiliev AA. Evolution of hybrid forecasting models. In Proceedings of the Mathematical Methods and Instrumental Systems in Economics and Education: Materials of the All-Russian Correspondence Scientific and Practical Conference; FGBOU VPO “UdGU”: Izhevsk, Russia, 2013; pp. 58–61.

88.

Golovchenko VB, Noskov SI. Combining forecasts with expert information. Autom. Telemech. 1992, 11, 109–117. [Google Scholar]

89.

Chuev YV, Mikhailov YB, Kuzmin VI. Forecasting Quantitative Characteristics of Processes; Soviet Radio: Moscow, Russia, 1975; p. 398.

90.

Iberla K. Factor Analysis; Ivanova VM, Translator; Preface by Dubrova AM; Statistics: Moscow, Russia,1980; p. 398.

91.

Lawley D, Maxwell A. Factor Analysis as a Statistical Method; Blagoveshchenskiy YN, Translator; Mir: Grodno, Belarus, 1967; p. 144.

92.

Harman G. Modern Factor Analysis; Lumelsky VY, Translator; Braverman EM, Ed.; Statistics: Moscow, Russia,1972; p. 486.

93.

Bogdanov AI, Tulchin LG. Forecasting product quality using factor analysis. In Methodology of Development of Control Systems: Models, Methods, Tools; VNIIMIUS: Lviv, Ukraine, 1987.

94.

Nosova NS. Forecast of characteristics of promising samples of technical products based on factor methods. In Proceedings of the III Siberian Scientific and Practical Conference on the Reliability of Scientific and Technical Forecasts: Abstracts of Reports, Novosibirsk, Russia, 9–11 September 1984; pp. 170–172.

95.

Bogdanov AI, Tulchin LG. Method of minimizing the number of indicators in quality management of electrical measuring equipment. Publication in Proceedings of the VNIIEP “Management Improvement, Scientific Organization and Labor Rationing in the Sub-Sector”; Saint-Petersburg, Russia, 1981; pp. 110–117.

96.

Bogdanov AI, Tulchin LG. The study of accuracy in the construction of communication models of individual quality indicators of electrical measuring equipment. Publication in Proceedings of the VNIIEP “Metrology, Quality, Reliability and Standardization of Electrical Measuring Equipment”; Saint-Petersburg, Russia, 1981; pp. 104–110.

97.

Bogdanov AI, Tulchin LG. Reduction of the dimension of the vector of correlated variables by discrete optimization methods. In I All-Union Meeting on Statistical and Discrete Analysis of Non-Numeric Information, Expert Assessments and Discrete Optimization: Abstracts; KazGU: Alma-Ata, Kazakhstan, 1981; pp. 22–23.

98.

Bogdanov AI, Tulchin LG. Method of product quality assessment according to “leading” indicators. In IV All-Union Scientific and Technical Conference “Metrological Maintenance of Machine-Building Industries of the National Economy; VNIIMS: Moscow, Russia, 1987.

99.

Bogdanov AI, Tulchin LG. Evaluation of the effectiveness of factorization in information processing by factor analysis methods. In II All-Union Conference on Statistical and Discrete Analysis of Non-numerical Information and Expert Assessments: Abstracts; TPI: Moscow, Russia, 1984; pp. 282–283.

100.

Bogdanov AI. Simulation modeling of random correlation matrices for evaluating methods of reducing the dimension of the vector of correlated variables. Publication in Collection of Scientific Papers of VNIIEP “Automation of Production and Control in Electrical Engineering”; Saint-Petersburg, Russia, 1984; pp. 126–133.

101.

Bogdanov AI. Modeling of data processing processes in automated control systems when evaluating the effectiveness of a heuristic algorithm for minimizing the number of quality indicators of electrical measuring equipment (EIT). In Information and Measurement Systems and Accuracy in Instrumentation: Abstracts of Reports”; MIEM: Moscow, Russia, 1982.

102.

Kovalchuk LA, Chernyshev IV, Yu V. Assessment of the quality of probabilistic forecasts (review). Automation. Belarus 1987, 1, 26–31. [Google Scholar]

103.

Kuznetsova KS, Golodnenko VN. On the question of quantifying the accuracy of the forecast (on the example of forecasting labor productivity). Econ. Math. Methods 1971, 7, 843–849. [Google Scholar]

104.

Bogdanov AI, Tulchin LG. Study of model stability in assessing the reliability of forecasts. In Proceedings of the Abstracts of the IY Siberian Scientific and Practical Conference on the Reliability of Scientific and Technical Forecasts, Novosibirsk, Russia, 14–16 October 1987; GPNTB SB of the USSR Academy of Sciences: Novosibirsk, Russia, 1987; pp. 176–177.

105.

Bogdanov AI. On the issue of stability of mathematical forecasting models. In Proceedings of the Collection of Scientific Papers on the Results of the International Scientific and Practical Conference “Modern Achievements and Developments in the Field of Economics and Management”, Orenburg, Russia, 25 September 2019.

106.

Bogdanov AI. Series 1: Natural and Technical Sciences. In Statistical Stability Tests of Mathematical Forecasting Models; Bulletin of the St. Petersburg State University of Technology and Design: Saint-Peretsburg, Russia, 2019; No. 4; pp. 9–13.

107.

Bolch B. Multidimensional Statistical Methods for Economies; Plitmanna AD, Translator; Preissl. S.A. Aivaziana; Statistics: Moscow, Russia, 1979; p. 317.

108.

Kremer NS, Putko BA. Econometrics: Textbook for University Students, 3rd ed; reprint. UNITY-DANA: Moscow, Russia, 2010; p. 328

109.

Historical Materials. Available online: https://istmat.info (accessed on 10 January 2024).

110.

Federal State Statistics Service. Available online: https://rosstat.gov.ru (accessed on 10 January 2024).

111.

Nikitina LN, Kraikina EA, Kasumova NM. Series 4: Industrial Technologies. In The Direction and Prospects of the Development of the Raw Material Base of Textile Products at the Present Stage; Bulletin of the St. Petersburg State University of Technology and Design: Saint-Peretsburg, Russia; 2022; No. 2. pp. 59–63.

112.

Andreev AV. Artificial intelligence and its role in big data processing. Smart Digit. Econ. 2023, 3, 65–69. [Google Scholar]

113.

Arkhipova LI. Big data and artificial intelligence in business: Development and regulation. In BIG DATA and Advanced Analytics = BIG DATA and High-Level Analysis: Collection of Materials of the VI International Scientific and Practical Conference; Bestprint: Minsk, Belarus, 2020; pp. 122–127.

114.

Belova MS. Artificial intelligence in the analysis of large data. Bull. Plekhanov Russ. Univ. Econ. 2021, 11, 136–141. [Google Scholar]

115.

Piletskaya AV. Artificial intelligence and big data. Young Sci. Kazan Russ. 2019, 50, 20–22. [Google Scholar]

116.

Popov DV. The mistaken man and big data: from the brain to artificial intelligence. Innov. Sci. Educ. Tolyatti Russ. 2019, 2, 89–96. [Google Scholar]

117.

Zhang T. The current state and development of artificial intelligence and big data. Innov. Sci. Educ. Tolyatti Russ. 2022, 50, 2436–2446. [Google Scholar]

Intelligent and Sustainable Manufacturing